基于蚁群算法的出行者路径选择行为

张福龙

(天津公路工程设计研究院, 天津 300000)

当前交通环境复杂多变，出行者在考虑出行路径的过程中除主观因素外容易受外部环境影响，在短时间内快速预测出行者的选择行为可为动态交通分配提供理论支撑，国内外学者对此进行了大量研究。文献[1]从出行者心理学的角度出发，考虑交通系统的不确定性、出行者感知误差及建模者观测误差分析出行者选择路径的过程。文献[2]采用路径均值设计更新蚁群算法，采用新的信息素更新方式用于指导出行者的选择路径。文献[3]设计包含臭味信息素的蚁群算法，可以同时考虑系统和出行者之间的效益。文献[4]运用蚁群算法分析交通拥挤条件下的出行者路径选择问题。文献[5]提出混沌蚁群算法，该算法更加适用于出行者连续性的选择路径。文献[6]提出一种欧式距离作为启发因子，运用模糊蚁群算法寻找最小能量的路径规划。如何短时间快速的预测出行者的路径选择行为是解决城市交通问题的一大瓶颈，本文利用蚁群算法具有分布式计算的特点和概率选择公式模拟出行者选择路径的行为，以期减少交通拥堵现象。

1 蚁群算法

蚁群算法的最大特点在于蚂蚁选择路径的过程中采用概率选择方式，根据路径信息素浓度和路径长短来选择。文献[7-8]首次提出蚁群算法并给出蚂蚁选择路径的公式:

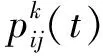
1.1 信息素更新策略

通过设计路径上的信息素更新方式可以设计不同性能的蚁群算法。文献[9]提出最大最小蚁群算法，将每条路径信息素的大小限制在[τmin，τmax]以防止搜索过程的停滞。这种设置可以防止路径的信息浓度过大或过小，比较符合出行者实际出行过程的实际路网情形，当出行路径不存在交通量时，设置出行路径的信息素浓度为最大值τmax；当路径发生交通拥堵时设置路径的信息素浓度为最小值τmin。

为了缩小流量在空间分布的差异性，加快算法的收敛速度，对传统蚁群算法进行改进，引入信息素平滑和信息素蒸发机制。改进后的蚁群算法只对最优路径上的信息素实行信息素蒸发机制，非最优路径上的信息素实行信息素平滑机制，因此有：

τij(t+1)=τij(t)+(1-ρ)(τmax(t)-τij(t))

，

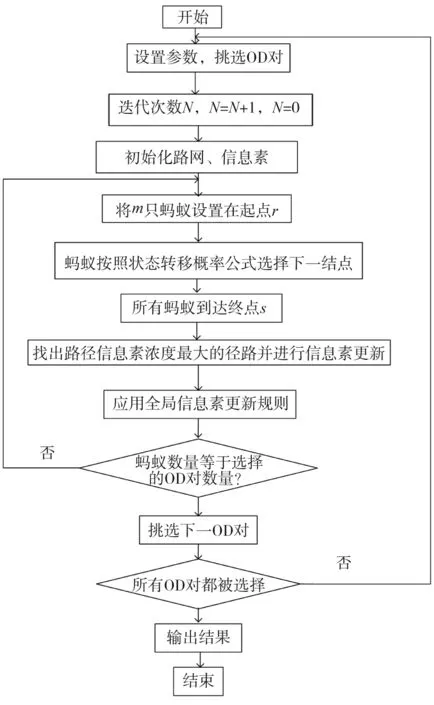
图1 算法流程

1.2 算法的适用性分析

蚁群算法在交通规划领域主要用于寻找最优路径[10-24]，算法流程如图1所示。利用蚁群算法的概率选择公式并结合用户均衡第一原理[25]，假设出行者具有相同的路径决策规则，传统模型大多以路径的出行阻抗最小或者路径的广义费用最少作为决策规则。出行者在选择路径的过程中考虑出行路径的广义费用，将路径的广义费用相反数定义为路径的信息素浓度，能够较好的模拟出行者选择路径的过程，则有

Tij=Tij(0)[1+a(v/c)b]Ft+pij，

τij=1/Tij，

式中：Tij为路段ij上的广义阻抗；Tij(0)为路段ij上的自由流行驶时间；v为通过路段的车流量，c为道路通行能力,v/c为路段ij上的交通量饱和度；pij为车辆通过路段ij的通行费(元)；Ft为车辆的时间价值(元/(h·车))；a、b为阻滞系数，a=0.15，b=4。

当出行者的决策过程受到外部极端条件影响时，如天气原因导致道路实际通行能力下降，出行路径广义费用陡然增大。在此情况下采用臭味信息素更新机制，臭味信息素可以不同程度的减弱正常的信息素浓度，有

τij(t+1)=γτij(t),γ∈[0,1]，

式中：γ为臭味信息素作用强度系数。

2 案例应用分析

图2 路径选择

构造如图2所示的交通路网，根据出行者的个体特征通过调节参数α、β的大小摸拟不同出行者的个体特征，对路径选择结果的差异。先后分4次让出行者选择路径，针对不同的出行者，参数α、β采用不同的取值，最后分析模拟出行者选择路径的过程。

当α=1，β=1，ρ=0.95时，t1、t2、t3、t4时刻的出行量分别为17 811、23 747、29 683、34 286 pcu(当量交通量)。根据已知数据，利用EXCEL软件进行编程进行计算，计算步骤如下：

1)确定从起点1到终点5有12条有效路径，分别为G1G2(1，2，5)、G1S2(1，2，5)、S1S2(1，2，5)、S1G2(1，2，5)、G3G4(1，3，5)、G3S4(1，3，5)、S3S4(1，3，5)、S3G4(1，3，5)、G5G6(1，4，5)、G5S6(1，4，5)、S5S6(1，4，5)、S5G6(1，4，5)。计算各条路径的广义费用，进而计算出各条路径的初始信息素浓度。

2)判断路网中各个路径的信息素浓度，计算t1时刻出行者选择路径的概率。计算结果如表1所示。

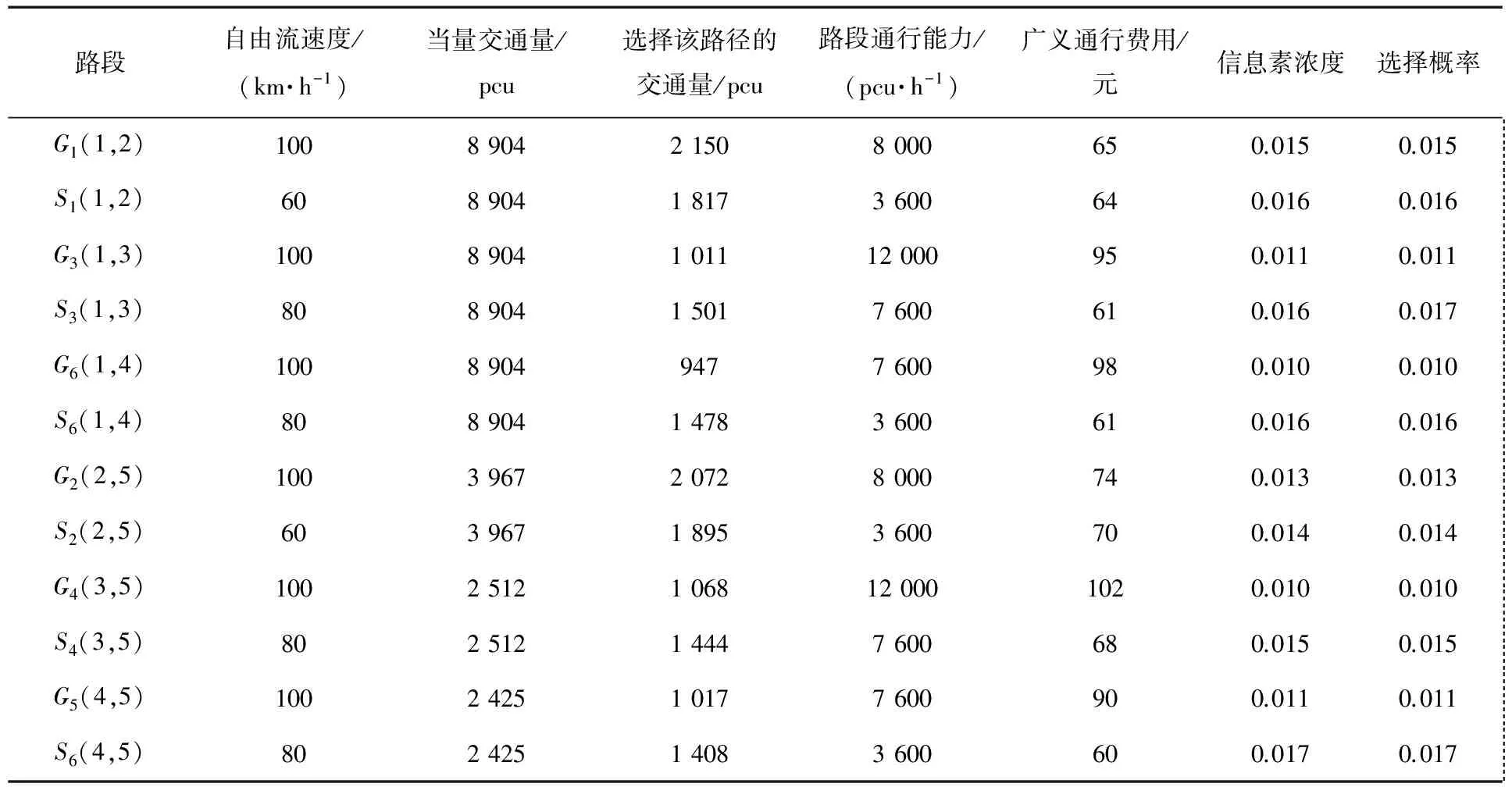
表1 t1时刻出行者选择结果

3)重新计算更新路网整体的信息素，分配t2时刻的出行者。

4)重复步骤2)3)，直到所有出行者选择了出行路径。t1、t2、t3、t4时刻出行者选择路径结果见表2。

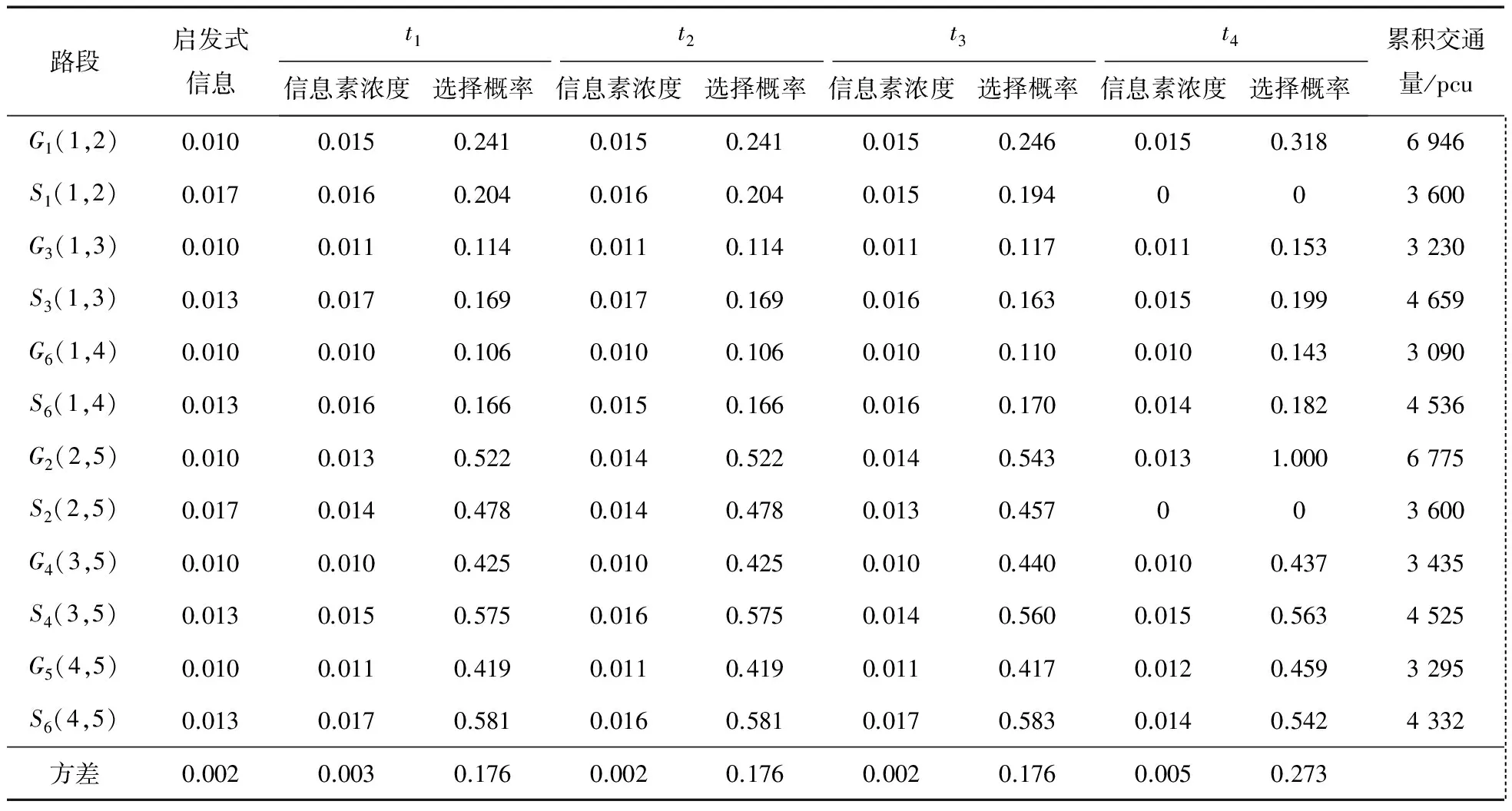
表2 出行选择结果

当路段S1(1，2)、S2(2，5)的v/c为1时，交通发生拥堵情况(v/c为1时，路段饱和代表交通拥挤)，臭味信息素开始发挥作用，导致下一时刻出行者选择路径时，路段S1(1，2)、S2(2，5)的信息素浓度为0，路段S1(1，2)、S2(2，5)被选择的概率为0，见表2。由表2可知：t1、t2、t3时刻各条路径的交通量未达到饱和状态，各条路径被选择概率大小的差异性逐渐缩小，出行者的空间分布更加均匀。分析每个时刻路径的信息素浓度，总结得出各条路径的信息素变化情况如图3所示。

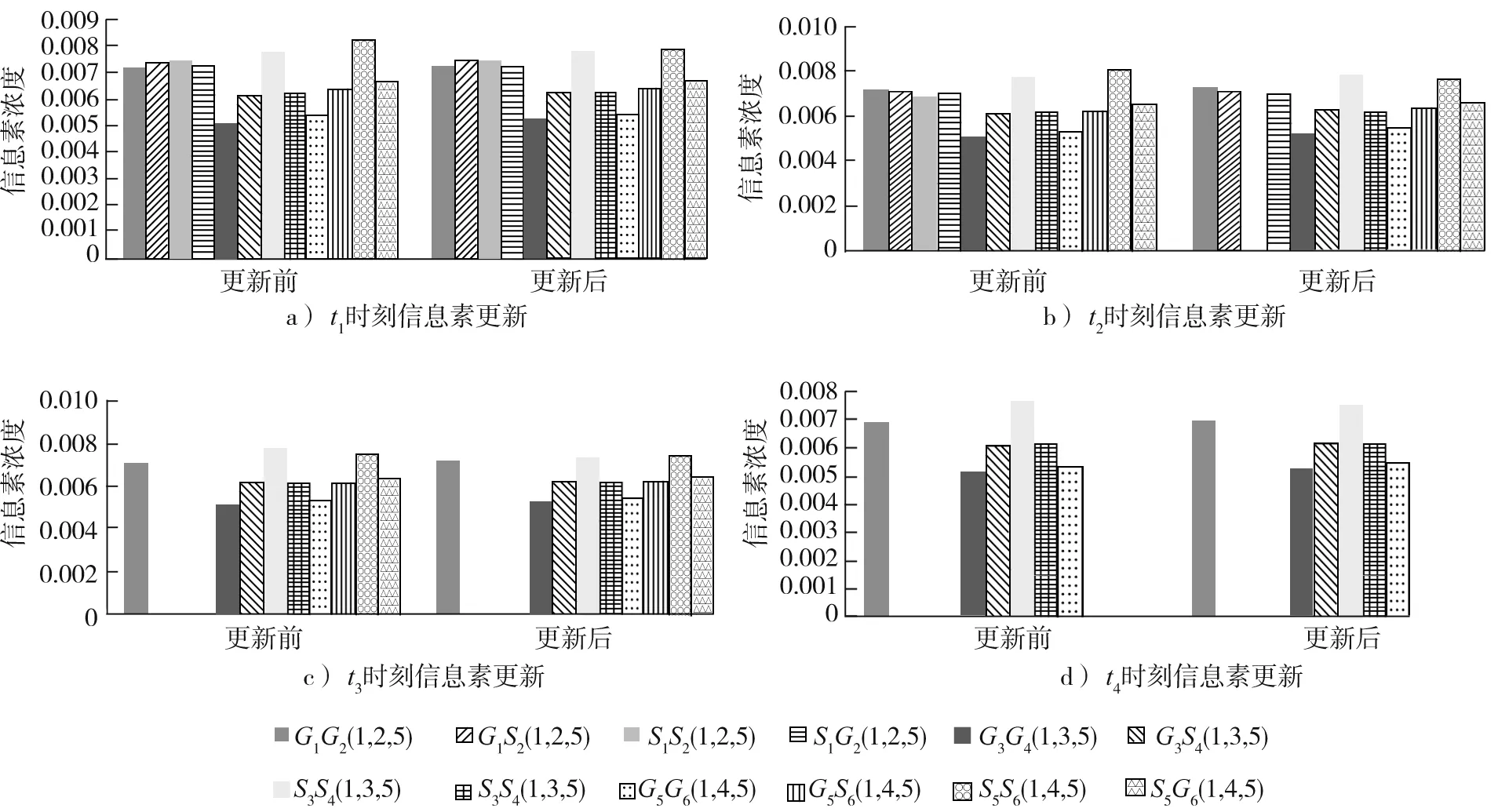
图3 有效路径信息素更新过程

3 结果分析

保持α=1不变，β由0～2逐渐增大，各条路径分担率的波动情况如图4所示。由图4可知：当β由0～2逐渐增大时，出行者的空间分布更加均匀。

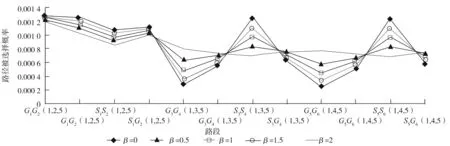
图4 β变化对各条路径分担率大小的影响

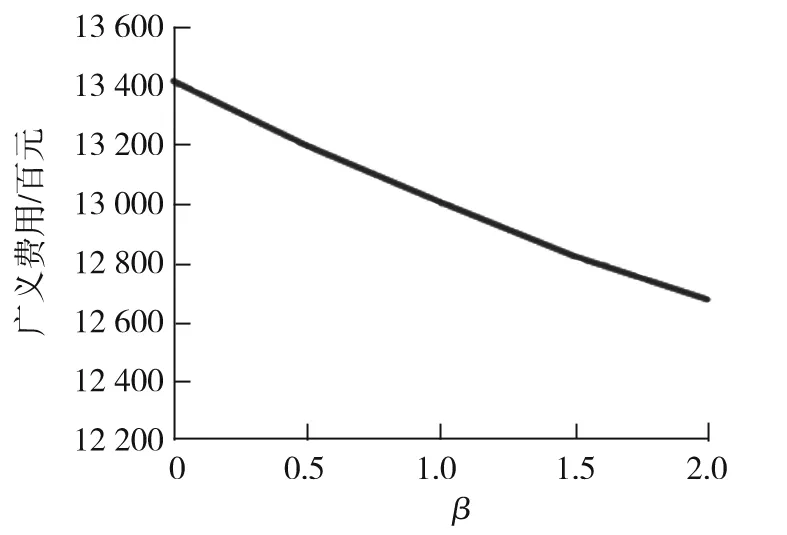
图5 路网流量广义费用估计值随参数的变化

保持α=1不变，β由0～2逐渐增大，用各条路径的广义通行费用之和作为整体路网费用的估计值，计算4个时刻路网的广义费用，结果如图5所示。由图5可知：随着参数β的增大，路网费用不断减小。

4 结语

采用改进蚁群算法并通过信息素平滑机制建立路径各条路段的联系，根据不同出行者的特征合理确定启发信息素的重要程度α与信息素的重要程度β，能使路网的广义通行费用逐渐减小并且出行者的空间分布更加均匀，因此，改进的蚁群算法能够较好的模拟出行者的路径选择过程。