基于数形结合思想的线性代数教学实践
2018-07-30高敬华
滕 旭,高敬华
(1. 云南大学 旅游文化学院,云南 丽江 674100; 2. 邓州市穰东高级中学校,河南 邓州 474100)
数学总体可以分为代数、几何、解析几何(又称代数几何)。解析几何是用代数的方法研究几何问题的学科,建立方程与曲线的关系,利用方程将图形研究定量化,以数为工具,以形为目的,这是典型的数形结合。尽管代数和几何研究的重点分别为数和形,但从未完全割裂。例如,代数中的实数与数轴、方程的根与函数的零点、函数及其图像、二元一次不等式表示平面区域等问题无不与图形相关,几何图形中的角度、距离等须用数字表示。数形结合可以使抽象的代数问题直观化、几何问题定量化[1]。
线性代数的研究对象之一是线性方程组,主要是线性方程组解的判定、解的表示。解的判定工具有行列式和矩阵。通过行列式的计算和克莱姆法则可以判定方程组是否有唯一解,并可得到唯一解。利用矩阵的秩可以判定线性方程组解的3种情况,即有唯一解、有无穷多解、无解。线性方程组解的本质是向量。通过研究向量的线性相关问题可以解决解的结构和解的表示问题。许多学者对线性代数教学的几何直观化进行了研究。王海侠、孙和军、石霞研究了几种变换的几何意义,并通过MATLAB软件给出了三元线性方程组解的几何意义(注:未区分三元线性方程组无穷解的两种情况)[2]。章晓研究了行列式的几何意义,但未能给出克莱姆法则的几何意义;借助直线、平面的关系研究了线性方程组解的判定问题,但未进行详细的推理论证[3]。韩瑞珠研究了线性相关及无关的几何意义[4]。滕树军、韩旭里探讨了线性代数教学几何直观化的必要性及其重要意义[5-6]。
笔者查阅了相关文献,通过总结整理,给出线性代数中的抽象概念在二维、三维情况下的几何解释,从图形直观方面解释线性代数的主要理论。
1 行列式的几何意义及克莱姆法则的几何解释
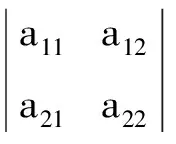
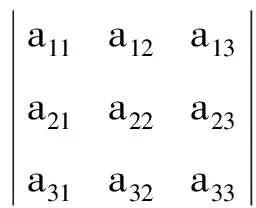
克莱姆法则的几何解释:对于二元线性方程组
即
x1α1+x2α2=β,
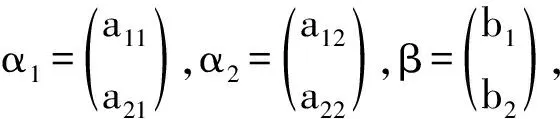
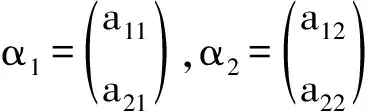
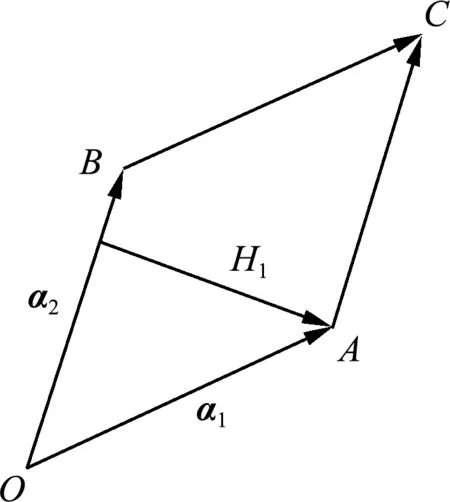
图1 二阶行列式的几何意义
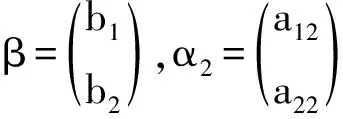
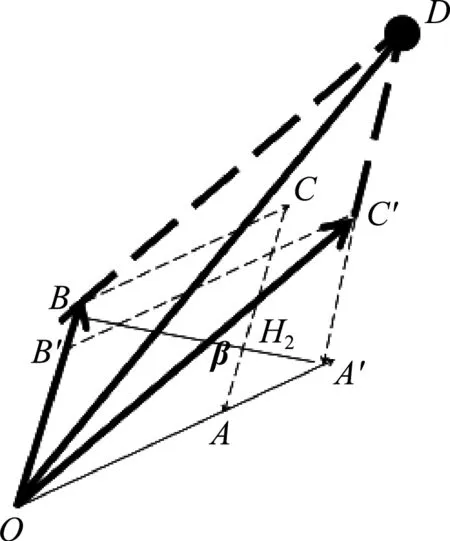
图2 二元线性方程组克莱姆法则的几何意义
图2中,

显然,S1=|x1|S,即
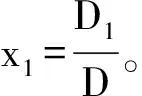
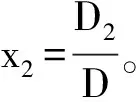
对于三元线性方程组
即
x1α1+x2α2+x3α3=β,
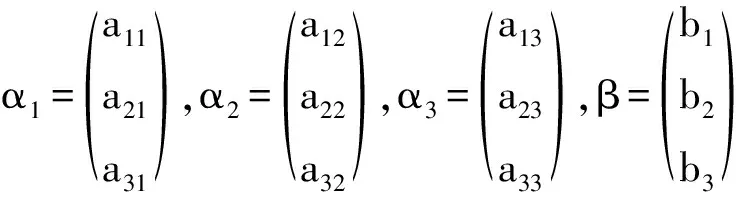
Dj(j=1,2,3)是行列式D的第j列元素αj由常数列β替换得到的行列式。

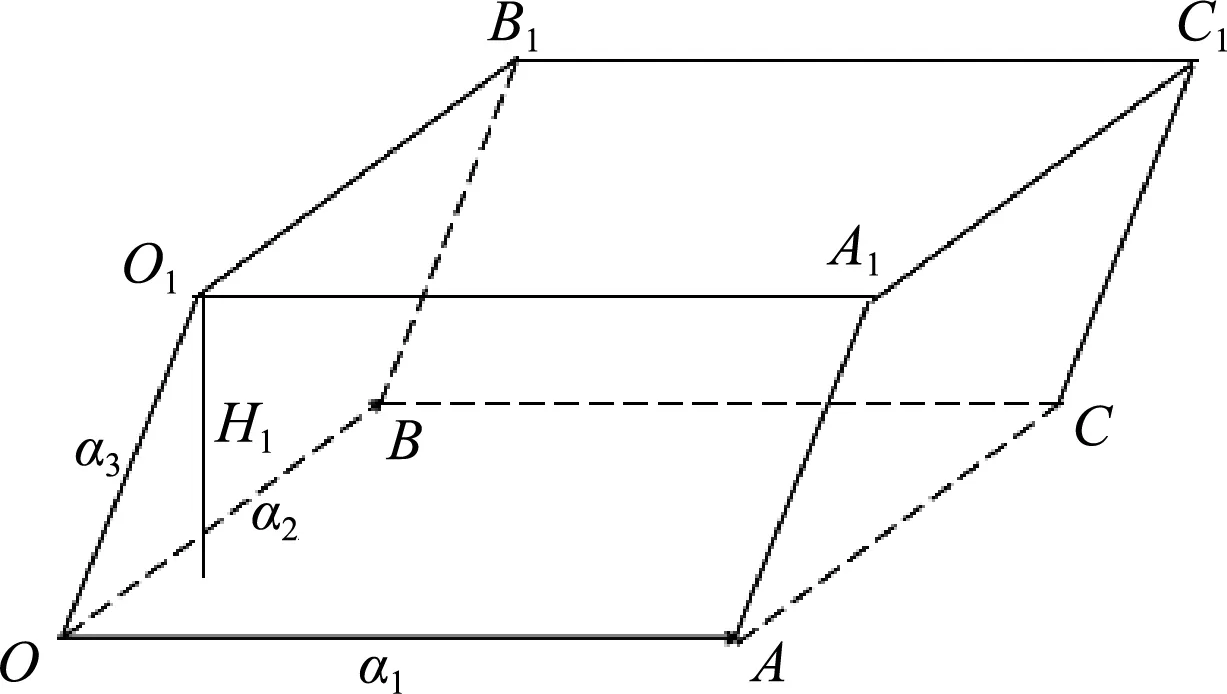
图3 三阶行列式的几何意义
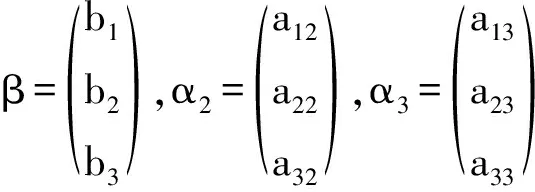
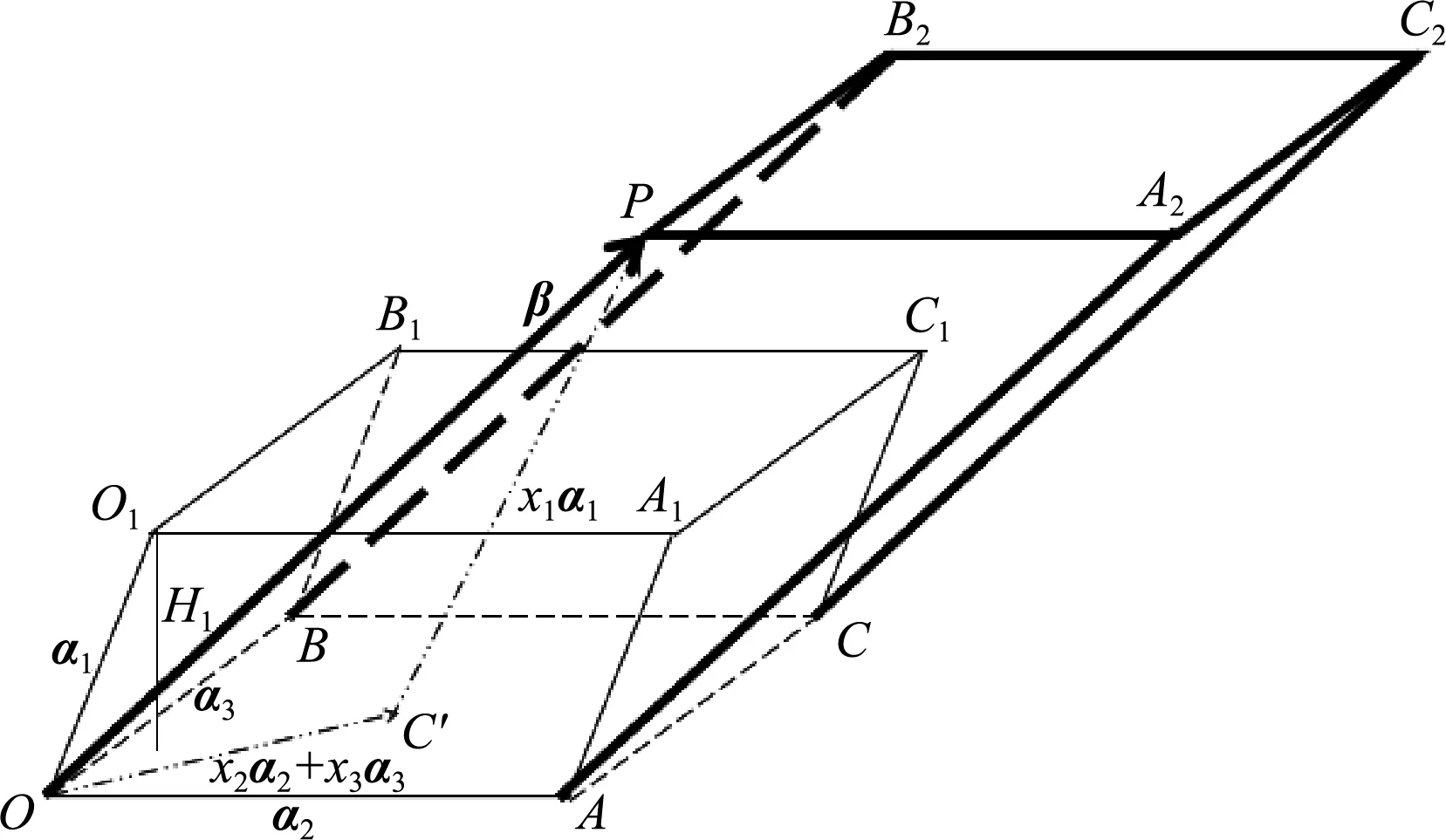
图4 三元线性方程组克莱姆法则的几何意义
图4中,
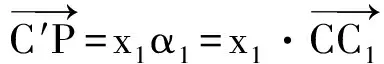
|C′P|=|x1|·|CC1|,
设H1,H2分别为点C1,P到平面OC的距离,显然有H2=|x1|·H1。
显然,V1=|x1|·V,即
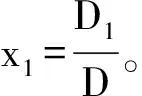
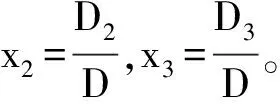
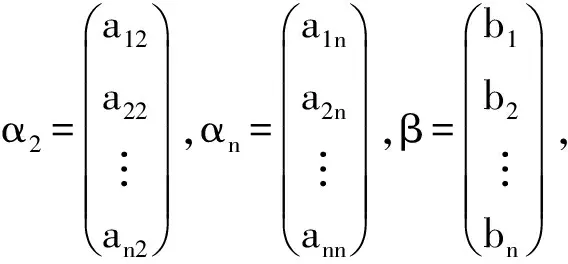
将以上二维、三维的结论推广。有n个方程的n元线性方程组
即
x1α1+x2α2+…+xnαn=β,
2 线性方程组解的判定理论的几何解释
对二元线性方程组而言,每个方程表示平面内的一条直线,因此二元线性方程组有解的几何意义是两条直线相交或重合,无解的几何意义是两条直线平行。二元线性方程组
中国的政治文化由礼乐来担当,无异于将审美提升到为政治服务的高度了,这是中国传统政治突出的特点。关于此,《乐记》有明确的表示。《乐记·乐论篇》说:“钟鼓干戚,所以和安乐也。”“乐至则无怨,礼至则不争,揖让而治天下者,礼乐之谓也。”中国古代将礼乐与天地相配,《乐记·乐论篇》云:“乐由天作,礼以地制。”“明于天地,然后能兴礼乐也。”联系到良渚祭天礼地活动,我们发现,中国祭祀、礼乐活动的雏形当在良渚已经具备。
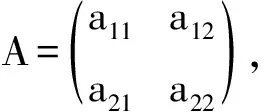
对三元线性方程组而言,每个方程表示空间内的一个平面,因此三元线性方程组有解的几何意义是3个平面有公共点,无解的意义是3个平面无公共点[3]。三元线性方程组
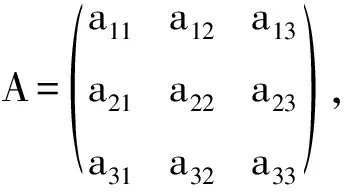
3个平面无公共点包括两种情况,即至少存在两个平面平行、两两相交且交线平行。
2) 3个平面两两相交且交线平行⟺任意两个平面所确定的空间直线互相平行⟺l1∥l2⟺r(A)=2≠r(A,b)=3⟺方程组无解。
3个平面有公共点包括3种情况,即3个平面重合(公共平面)、两两相交且交于同一条直线(公共直线)、两两相交且交于一点(唯一公共点)。
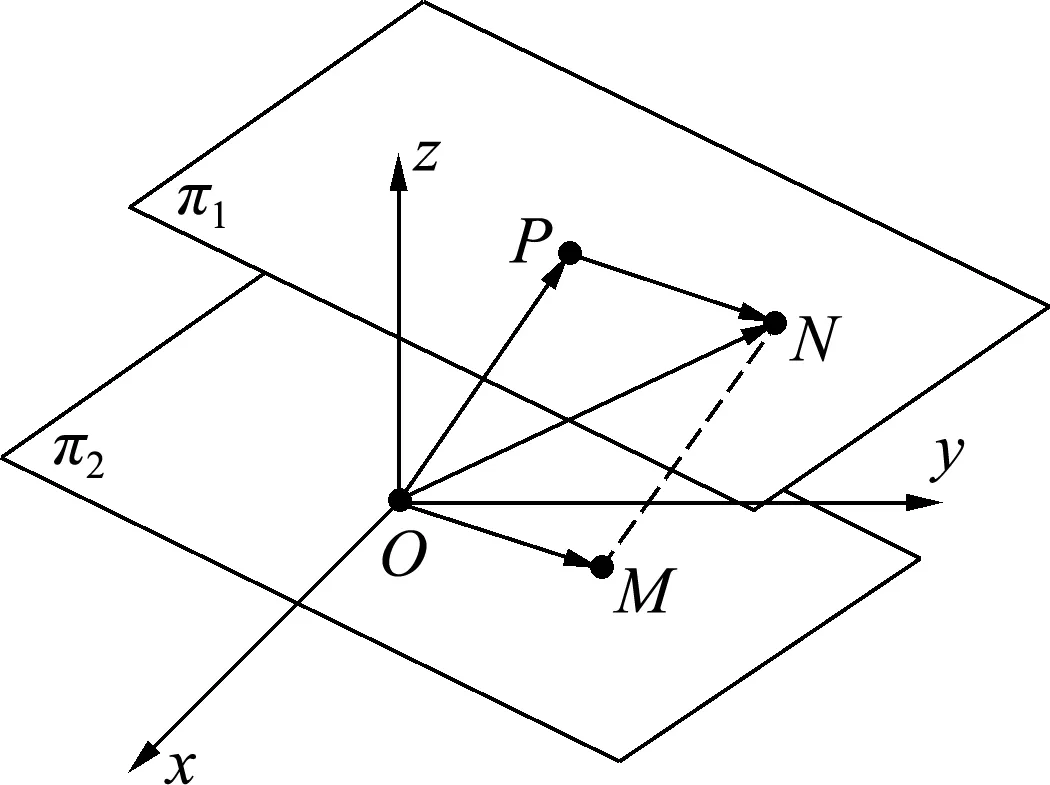
1) 3个平面重合⟺a11∶a21∶a31=a12∶a22∶a32=a13∶a23∶a33=b1∶b2∶b3⟺r(A)=r(A,b)=1 2) 3个平面两两相交且交于同一条直线⟺任意两个平面所确定的空间直线重合⟺l1与l2重合⟺r(A)=r(A,b)=2⟺方程组有无穷多解且解向量组构成直线,其秩为n-r=1。 3) 3个平面两两相交且交于同一点⟺任意两个平面所确定的空间直线交于一点⟺l1与l2相交⟺r(A)=r(A,b)=3⟺方程组有唯一解。 将以上二维,三维的结论推广,对于任意n元线性方程组 有解的充要条件是r(A)=r(A,b)。若r(A)=r(A,b) 二元线性方程组有无穷多解的几何意义是两条直线重合。 如图5所示。 图5 二元线性方程组全部解的几何表示 三元线性方程组有无穷多解的几何意义是3个平面交于一条直线或3个平面重合。 若3个平面交于一条直线,则r(A)=r(A,b)=2 如图6所示。 图6 三元线性方程组解的结构之几何意义1 如图7所示。 图7 三元线性方程组解的结构之几何意义2 将以上二维、三维的结论推广。对于任意n元线性方程组 若有无穷多解,则其全部解η=η*+ξ。其中η*为原方程组的一个特解,ξ为原方程组导出组的全部解。 对于二维向量来说,每个向量表示平面向量。 α1,α2,…,αn线性相关⟺存在两个向量αs,αt共线⟺存在两个向量αs,αt,有 αs=kαt 即 αs-kαt=0 成立⟺齐次线性方程组 x1α1+x2α2+…+xnαn=0 有非零解。特殊地,任意n(n>2)个二维向量,若其中两个向量共线,则向量组线性相关,若任意两个向量均不共线,根据平面向量基本定理,第3个向量必可由两个不共线的向量线性表示,所以向量个数n大于向量维数时,向量组必线性相关[4-6]。 对于三维向量来说,每个向量表示空间向量。 α1,α2,…,αn线性相关⟺存在3个向量αs,αt,αp共面⟺存在3个向量αs,αt,αp,有 αs=k1αt+k2αp 即 αs-k1αt-k2αp=0 成立⟺齐次线性方程组 x1α1+x2α2+…+xnαn=0 有非零解。特殊地,任意n(n>3)个三维向量,若其中3个向量共面,则向量组线性相关,若任意3个向量均不共面,根据空间向量基本定理,第4个向量必可由3个不共面的向量线性表示,所以向量个数n大于向量维数时,向量组必线性相关。 将以上二维,三维的结论推广,任意m维向量组线性相关的充要条件是齐次线性方程组 x1α1+x2α2+…+xnαn=0 有非零解。当n>m时,向量组必线性相关。 线性代数的概念比较抽象,教学中可以从二维、三维的角度给以几何直观,对于更高维的代数问题,直观的几何解释不再存在。引导学生牢固掌握基础知识,强化直觉思维能力,把低维下形成的认识推广,有助于他们理解抽象概念,取得较好的学习效果[5-6]。3 线性方程组解的结构的几何解释
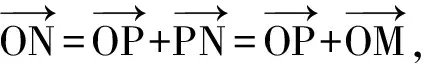
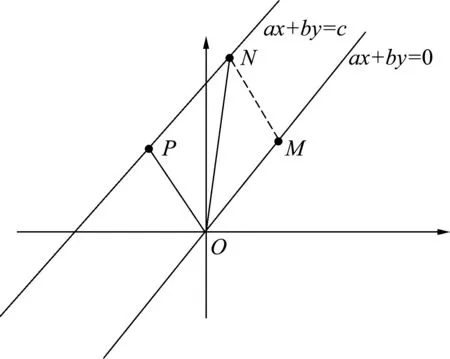
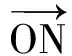
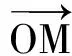
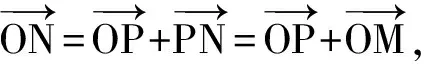

4 线性相关与线性无关的几何解释
5 结束语
