热冲击作用下圆柱体耦合热弹性分析

蔡 苏，方 勃

(沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136)

热弹性应力被广泛应用于航天航空工程实际问题中， 如零件在热应力作用下的强度、刚度等等问题，使热弹性应力的探讨具有越来越重要的意义。M.A.Biot[1]建立热弹性力学变分原理，但是温度场的变化不仅受热源、换热边界条件、传热系数等因素影响[2]，还取决于弹性应变，认为热传导方程与热弹性运动方程需联立耦合求解[3]。耦合效应增加了实际问题的求解难度，什么情况下可以将耦合项略去不计至关重要。B.A.Boley[4]等人引入耦合系数来讨论耦合影响。在计算耦合热弹性问题时，最常用方法是拉普拉斯变换，Y.Takeuti等[5-6]通过热弹性势函数和勒夫位移函数的引入探讨了轴对称耦合热应力问题，给出热应力的一般处理方法，该法在求解二维或三维的瞬态热应力问题非常实用[7-9]。同时热冲击问题受到广泛关注，外界加热条件的突变使物体产生非定常热应力，较高的应变率影响了温度场分布规律，所以耦合效应在热冲击问题中表现明显[10]。广义热弹性理论的耦合非线性控制方程的精确解存在于特殊边界条件下，当边界条件非理想化时，精确求解存在一定困难，于是J.T.Orden[11]等人利用了有限元法近似求解半空间耦合问题。随着对耦合效应理解加深，温度场、应变场、电磁场等多场耦合的研究为实际问题的解决提供了越来越多的帮助，也进一步发展了耦合热弹性应力地研究。

本文采用常用的金属材料分析，耦合项的影响比动力项大，所以可忽略动力项，模型变为拟静态形式，建立解析方法求解模型。基于热弹性理论，引入势函数将互耦的温度场与位移场分离为独立方程，采用Bessel方程、Laplace变换与留数定理求解[12]，研究了圆柱体受垂直于外表面的热冲击作用的热弹耦合问题。

1 模型建立

图1所示有限长均质各向同性圆柱体结构，长度为L，半径为a，沿圆柱体的轴向为柱坐标系当中的坐标轴Z轴，假定初始时刻t=0时，受到垂直于外表面的持续热冲击。

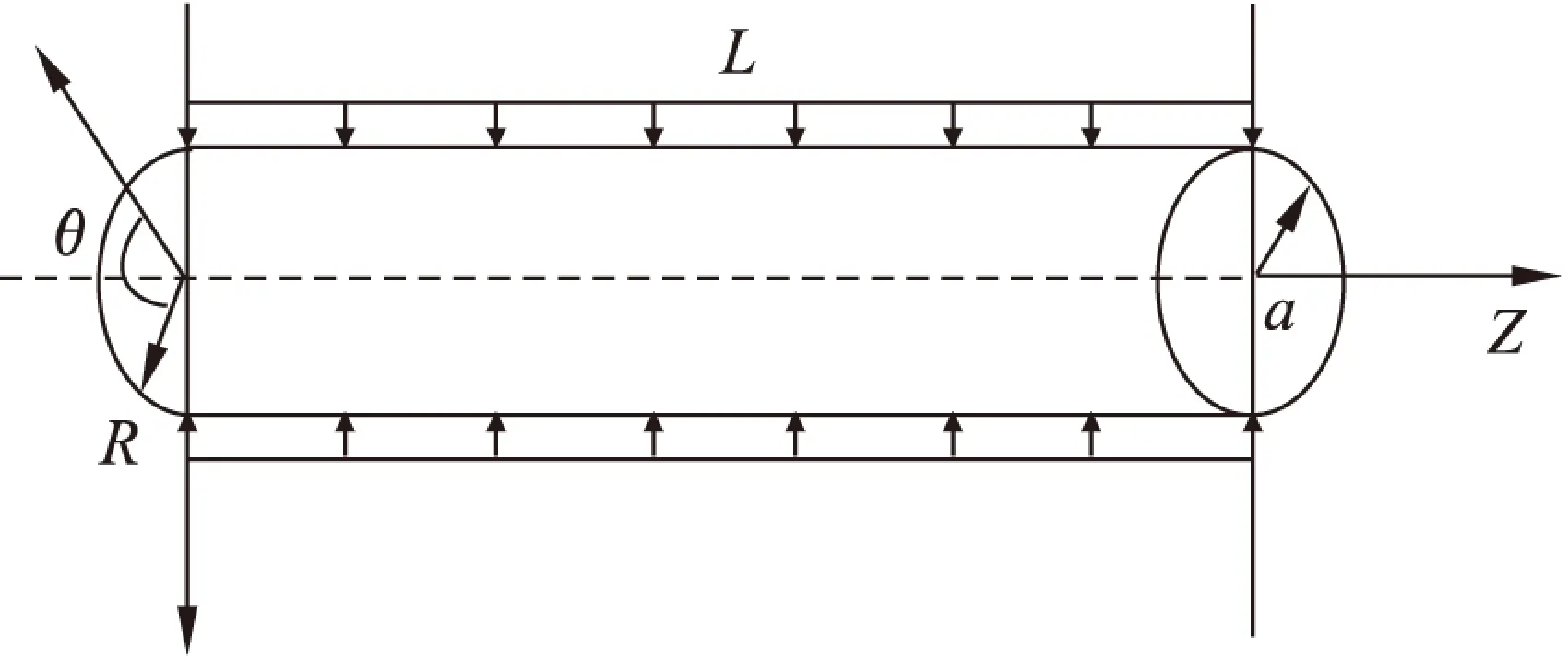
图1 圆柱体模型

圆柱体表面受热冲击属第一类热边界条件，初始条件和边界条件如下，其中TA为参考温度，T表示温度场，H[t]为Heaviside单位函数，h为相对换热系数

初始条件：t≤0时，T=0，ui=0，σij=0

(1)

边界条件：t>0及Z=0，Z=L时，T=0，u=0，σZ=0

(2)

对于均质的各同性体不考虑动力项和内热源[13]，则轴对称耦合热弹性控制方程为

拟静态热弹性方程

(3)

热传导方程

(4)

本构方程

(5)

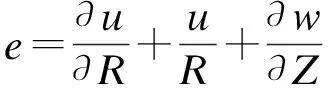
引入如下无量纲变量，以便简化求解以上方程

ρ=R/a，z=Z/a，l=L/a，τ=Ht/a2

(6)

(7)

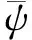
(8)

将(8)中的两个调和函数代入本构方程(5)及控制方程方程(7)当中可得

(9)

应用拉普拉斯变换与反变换求解以上方程，f(t)的象函数用f*(s)表示，则关于时间t的边界条件(2)的变换形式为

(10)

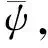
(11)

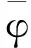
(12)

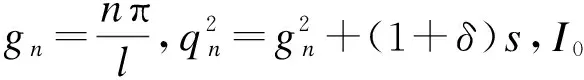
将式(11)、(12)分别代入到拉普拉斯变换后的u*和σ*中可得

(13)

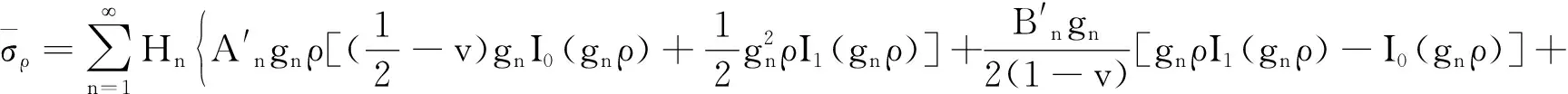
(14)

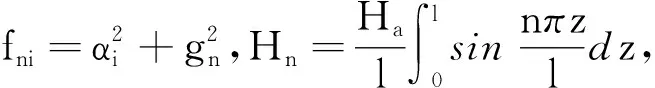
2 数值计算与分析

本文算例选取有限长圆柱体，讨论耦合效应对柱体内外部温度场、应力场影响，表1 给出了公式当中具体参数值(国际单位)。

表1 参数

通过数值仿真，分别对耦合与非耦合两种情况进行了分析，即耦合系数δ=0相当于非耦合，δ≠0相当于耦合，图2至图12中显示了温度场与应力场的变化情况。图中用虚线表示耦合，实线表示非耦合，为计算简便并在保证精度的情况下取n=6。

图2 温度场沿径向变化图

由图2～4可知，在z=5截面上，当ρ值较小时，温度随τ值减小而增大，当ρ值大于0.3时，温度随着τ值增大而增大，且趋于一稳定值收敛，耦合与非耦合差异变小；当τ值较小时，外部温度大于内部且温差较大。随着τ值增大,外部与内部温差逐渐减小。耦合与非耦合差值随着τ值增大逐渐减小且趋近于重合，符合实际情况。

图3 温度场沿轴向变化图

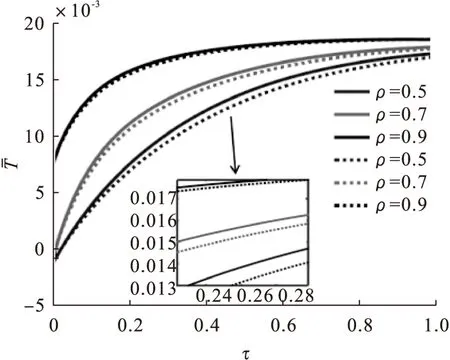
图4 温度场随时间变化图

图5 径向应力沿径向变化图

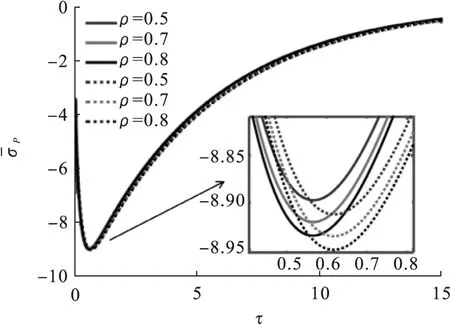
图6 径向应力随时间变化图

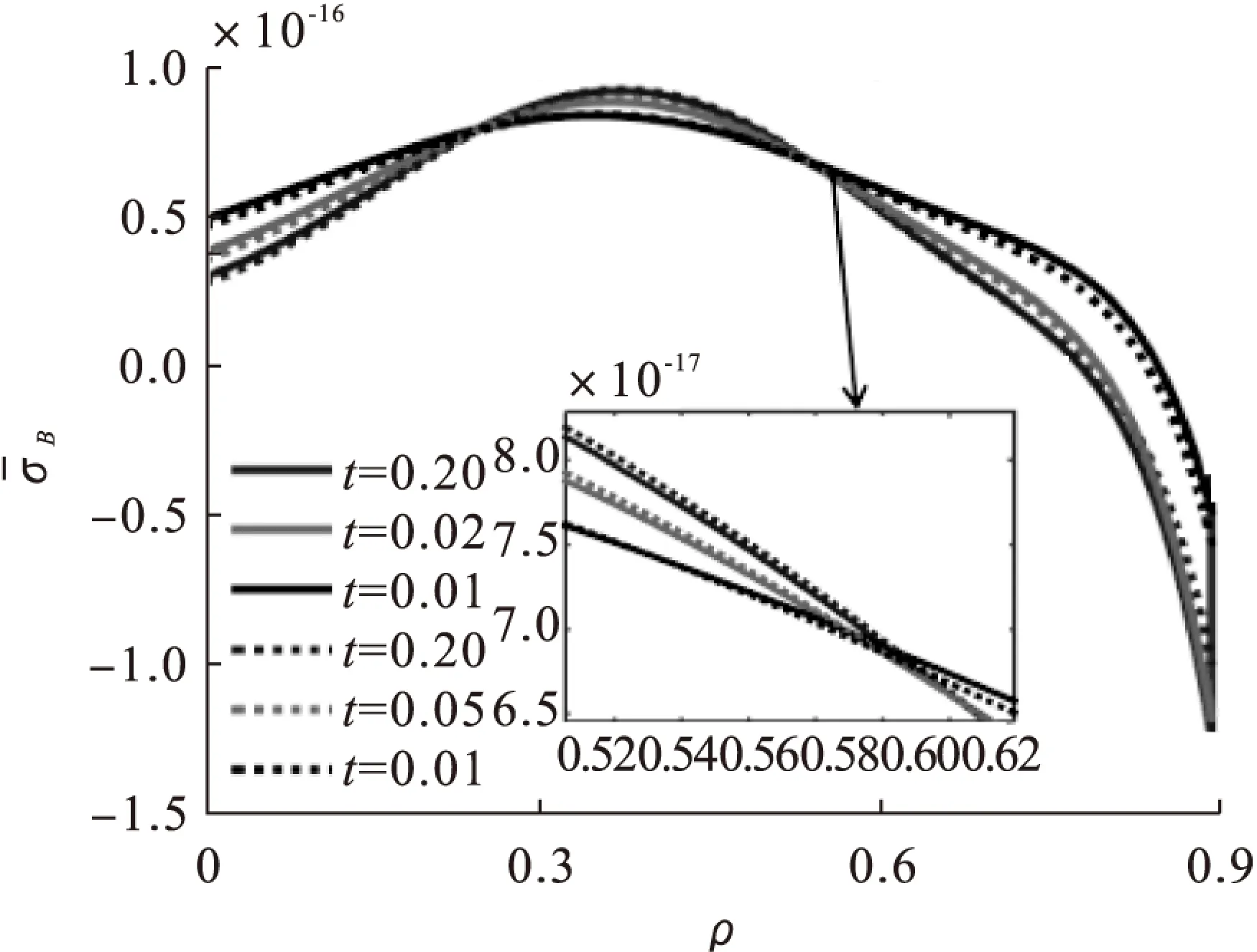
图7 环向应力沿径向变化图

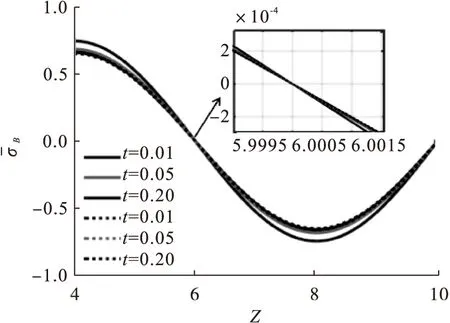
图8 环向应力沿轴向变化图

由图5～6可知，在z=5的截面上，径向应力表现为压应力。压应力由内部到外部沿径向的值逐渐减小，且值趋近于0。当τ值较小时，其值也大，τ约为0.6时应力值达到峰值,然后随着τ值增大而逐减小。在τ约为 0.1时，耦合与非耦合差异较大。

由图7～9可知，横截面上环向应力变化规率，柱体内外部有拉压力到压应力的转变，在z=5的截面上，拉应力值随着τ先增大后减小，且趋近于稳定，τ值约在0.2时应力值达到峰值。耦合与非耦合差异值分别随z、ρ值的变化都发生符号改变。

图9 环向应力随时间变化图

图10 轴向应力沿径向变化图

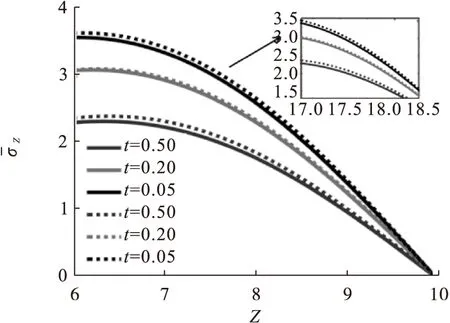
图11 1柱体外轴向应力变化图

由图10～13可知，柱体中间截面上, 轴向应力的分布由于柱休外部温度高于内部,柱体外部呈拉应力区，内部呈压应力区，是外部材料受热膨胀而受到挤压的结果，以及随τ值的变化规律与环向应力类似。当τ值约为0.5时，拉应力与压应力的区域逐渐趋向稳定。且τ值增大，应力趋向于0，耦合与非耦合差异值分别随z、ρ、τ值的变化发生符号改变。

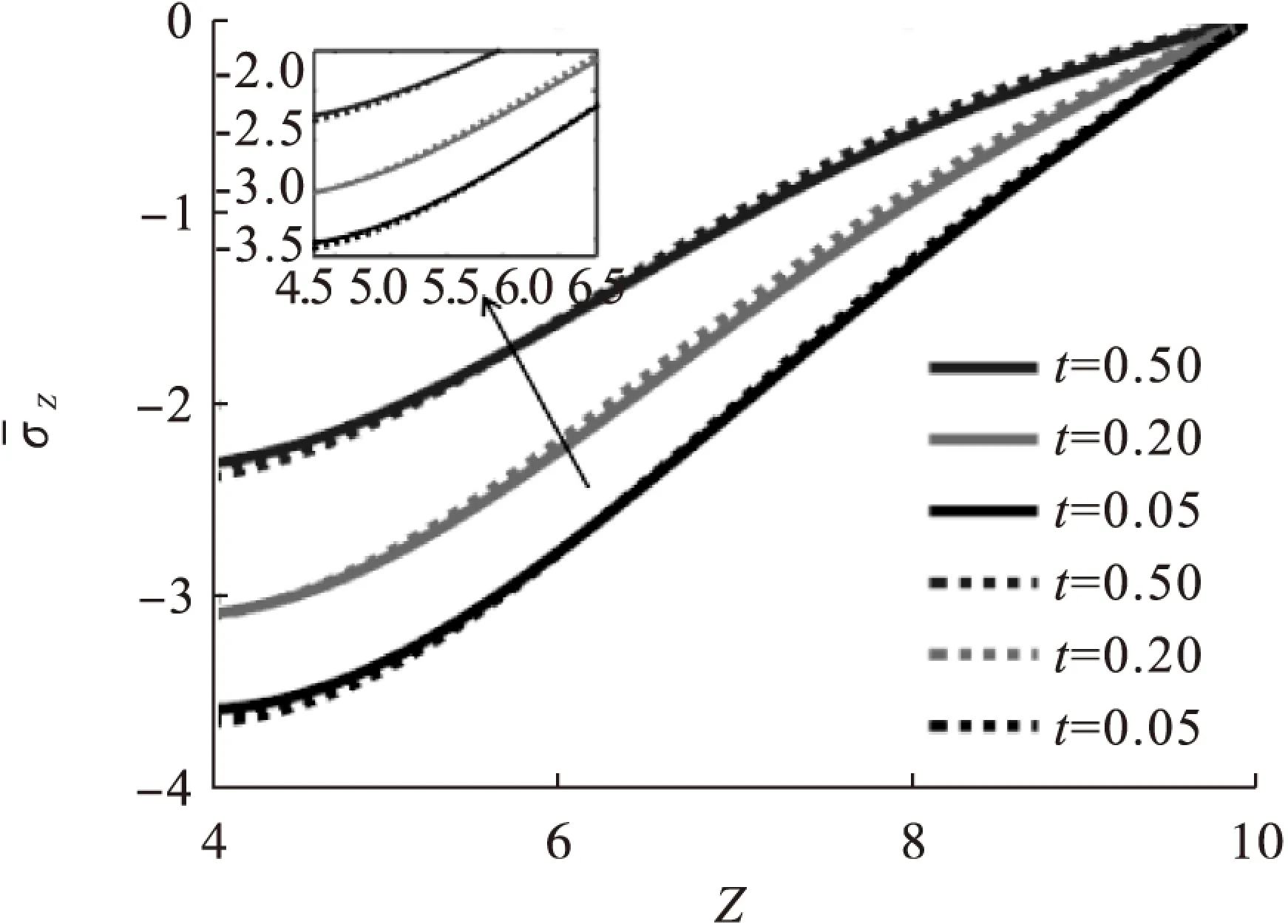
图12 2柱体内轴应力变化图

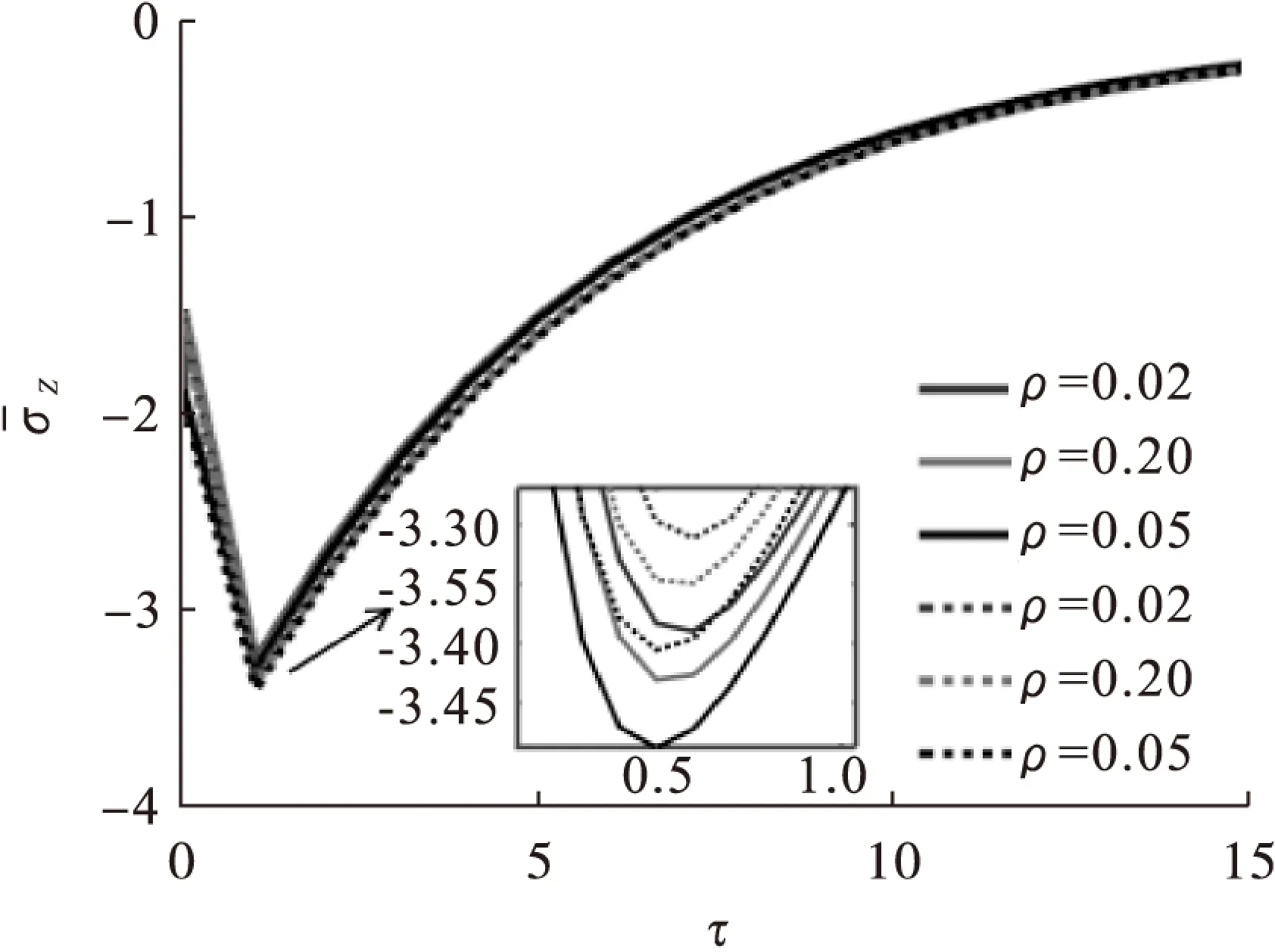
图13 轴向应力随时间变化图

3 结论

耦合效应是解决工程热弹性问题的重要研究内容，本文建立了热冲击作用的圆柱体的热弹性耦合模型，引入两个调和函数并给出解析算法，通过算例仿真证明，严格推导出的解析解在整个时间域是有效的。因为所采用的耦合参数是金属的一个实际值，所以计算方法与数值结果也同样适用于工程问题。且结果证明，耦合与非耦合在分布图上表现出差异，温度分布上差异明显。