微尺度平面正交各向异性功能梯度压电板的弯曲模型
2018-07-30乔瑞,贺丹
乔 瑞,贺 丹
(沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室,沈阳 110136)
随着结构设备的微型化发展,由压电材料[1,2]所构成的微/纳米结构在近年来得到了极大的关注[3]。微/纳米尺度下的压电结构较其宏观状态拥有更新颖的力学、电学及其它物理/化学性能,常作为重要的零部件分布于微/纳米装置中,如纳米级的传感器、制动器以及发电机等[4-6]。在这些应用中,结构的几何尺寸范围可能从几百纳米到只有几纳米。诸多微试验证实[7,8],当材料进入到上述尺度时会产生所谓的“尺度效应”问题,而这会对结构的力学、电学响应产生显著的影响。对于此类问题的研究中,传统连续介质理论因为缺乏内禀参数而无法对尺度效应现象作出解释,因此人们发展了许多新的高阶理论来描述尺度效应,如应变梯度理论[9]、偶应力理论[10]、非局部理论[11]等。以上理论中,由Yang[12]提出的修正偶应力理论因其只含有一个材料尺度参数而独具优势并在此理论基础上建立了大量适用于分析微尺度梁/板力学问题的模型。柯燎亮[13]等人基于修正偶应力理论着眼于功能梯度材料的力学分析,建立了一系列功能梯度梁/板的弯曲[14]、非线性振动[15]、稳定性[16]模型。郑世杰[17]等人基于修正偶应力理论和高阶梁理论讨论了功能梯度压电微梁的弯曲和振动特性,在其工作中对比了不同梁理论对于计算结果的影响。Li[18]等在修正偶应力理论和正弦板理论基础上对微尺度功能梯度压电板进行了静力和动力学分析,并指出了功能梯度变化指数对尺度效应的影响。Mohammadimehr[19]等在修正偶应力理论的基础上探讨了在热、电和力3种工况下尺度效应对功能梯度压电微板屈曲和振动响应的影响。但由于修正偶应力只含有一个材料尺度参数,在以上学者的研究工作中仅是针对于横观各向同性的压电材料的力、电学性能进行了讨论。
近来,陈万吉[20]等提出一种新的修正偶应力理论,首次将偶应力理论拓展到对微尺度各向异性材料的分析当中。杨子豪[21-23]等则基于此理论研究了平面正交各向异性功能梯度梁/板的弯曲、振动以及屈曲问题。本文的主要目的是尝试基于该理论建立平面正交各向异性功能梯度压电板的弯曲模型。通过两个材料尺度参数、分别描述两个不同方向上尺度效应对结构弯曲刚度和电势能的影响。
1 基于新修正偶应力理论的功能梯度压电板
采用两种或两种以上材料所构成的微尺度平面正交各向异性功能梯度压电板的示意图如图1所示。假设该压电板的材料组分沿坐标z轴方向上连续且呈梯度变化,宏观材料属性(如弹性模量、剪切模量、压电系数、介电系数)遵循式(1)中幂律形式
Y(z)=YuVu(z)+YlVl(z)
(1)
其中:Yu和Yl分别代表上(z=h/2)、下(z=-h/2)表面的材料属性,Vu(z)和Vl(z)上、下表面材料所占的体积分数,r为功能梯度变化指数,h为板的高度,z为板内一点距板几何形心面的距离。
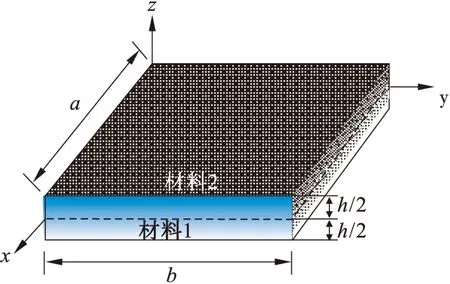
图1 功能梯度压电微板的几何尺寸
新修正偶应力理论[24]通过将曲率张量的非对称化,发展了一种可应用于各向异性材料的微尺度理论。将该理论引入到功能梯度压电材料的力学性能分析中可得以下关系
(2)
其中:ui为平动位移;θi为转动位移;εij和χij分别为应变张量和曲率张量;Ei为电场强度;Φ为电势函数;
压电材料的本构关系为
(3)
其中:σij和mij分别为应力张量和偶应力张量;Di为电位移;Cijkl(i,j,k,l=1,2,3)、eijk和μik分别为刚度矩阵、压电系数以及介电常数;Gi代表剪切模量;i和j分别为两个方向上的材料尺度参数,值得注意的是,新修正偶应力理论偶应力张量是对称的,曲率张量是非对称的。
2 位移场和本构方程
本文采用Kirchhoff薄板理论,位移场表达式为
w=w(x,y)
(4)
其中,u,v,w分别为板内任意一点沿x轴,y轴和z轴方向上的位移;u0,v0为板中面上一点沿x轴,y轴方向上的位移;φ为板中面的电势能;V0为作用在板上表面的外部电压,γ=π/h。
基于上述位移场和电势能场,得到非零的工程应变张量
(5)
曲率张量
(6)
电场强度
(7)
压电微板的本构关系可以表示为
(8)
(9)
(10)
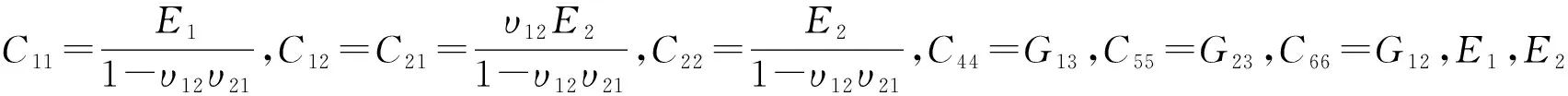
3 平衡微分方程及边界条件
基于虚功原理推导本文模型的平衡方程和边界条件。虚功原理可表述为
δU-δW=0
(11)
式(11)中:U为弹性体的内力功,W为外力功。
其中,内力虚功δU可以表示为
(12)
其中;A为板的面积分域,∂A为板边界封闭的线积分域,nx和ny为板边界外法线的方向余弦。N、Q和M为经典理论中板的内力和内力矩,Y为偶应力引起的内力矩,它们的具体表达式为
(NxMxNyMyQQ1YxYyYxyYyx)=

(13)
外力虚功δW可表示为
(14)
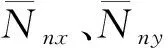
(15)
将式(12)、(14)、(15)代入到虚功原理中,可以得到内力表示的控制方程如下
(16)
相应的边界条件为

(17)
将方程(5)、(6)、(7)、(8)、(9)、(10)代入到方程(16)中,可得位移表示的平衡方程
(18)





4 算例分析
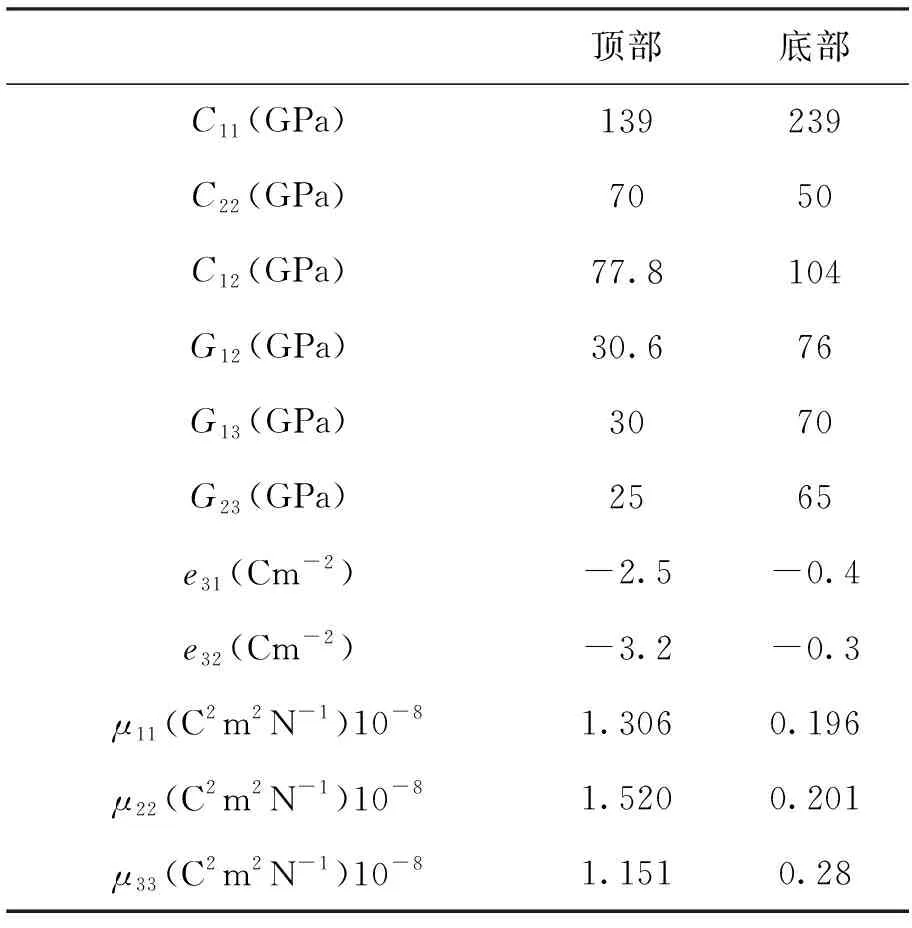
以双正弦载荷q=q0sin(πx/a)sin(πy/b)作用下的四边简支方板为例,分析其静弯曲特性及所产生电场强度的尺度效应。板的几何尺寸的表示分别为长a,宽b以及厚度h。材料的杨氏模量,剪切模量,压电系数以及介电常数假设为在厚度上以幂律形式呈连续变化,泊松比和材料尺度参数在厚度方向上为常数。
满足所有边界条件的位移试函数取为
(19)
式(19)中,α=mπ/a,β=nπ/b,(Umn,Vmn,Wmn,Φmn)分别为待定的傅里叶系数,将其代入到方程中可以得到准确的位移场函数。
将公式代入用位移表示的平衡方程中,得到以下的线性方程组
(20)
方程组中,kij(i,j=1,2,3,4)为耦合刚度矩阵,其具体表达式为:
k11=(C11)0α2+-(C66)0β2
k12=k21=-[(C12)0+(C66)0]αβ
k13=k31=(C11)1α3+[(C12)1+2(C66)1]αβ2
k14=k41=(E31)0α
k22=-(C66)α2-(C22)0β2
k23=k32=[(C12)1+2(C66)1]α2β+(C22)1β3
k24=k42=(E32)0β
k33=-[(C11)2+(
4(C66)2+(
k34=k43=-(E31)1α2-(E32)1β2
k44=H11α2+H22β2+(H33)2
(21)
4.1 尺度效应
本节算例主要目的为探究尺度效应对压电微板的弯曲挠度和电势能造成的影响。板的几何尺寸取为h=17.6 μm,a=10 h,功能梯度变化指数r=1,外电压V0=0,同时假设材料尺度参数l1=l2=l相等。材料参数见表1,弯曲挠度和电势能的无量纲处理方式为
(22)
4.2 微观各向异性对和的影响
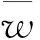
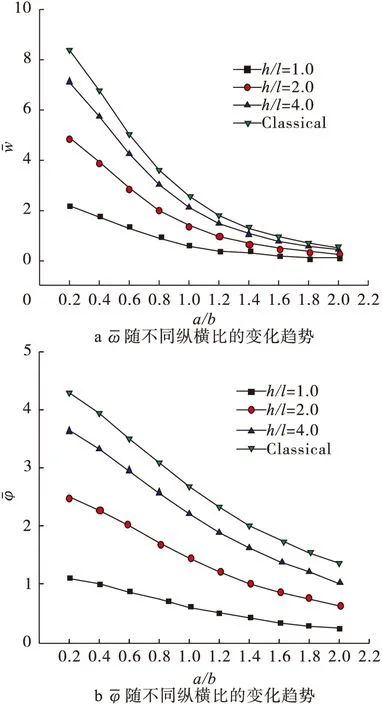
图2 无量纲弯曲挠度和电势能随不同纵横比的变化趋势
如图3所示的三维图,横轴为l1/h,l2/h,纵轴为板弯曲挠度和受弯所产生的电势能。从图3中可以看出,随着l1/h和l2/h比值的逐渐增加,压电微板的弯曲刚度逐渐变大,尺度效应越明显。而当l1/h和l2/h的比值趋近于0时,即压电微板厚度远大的于材料尺度参数时,尺度效应消失。同时值得注意的是,图3中由尺度效应所引起的压电微板弯曲挠度和电势能的改变程度在两个正交方向上是不一致的。这说明在研究微尺度各向异性材料的力学性能时,可能不仅仅要考虑材料宏观尺度上的各向异性,微观各向异性的影响也需要考虑在内。本文模型当沿正交方向上材料尺度参数l1=l2时,本文模型可退化为相应的各向同性偶应力压电微板模型,当l1=l2=0时,则退化为传统宏观压电板理论。
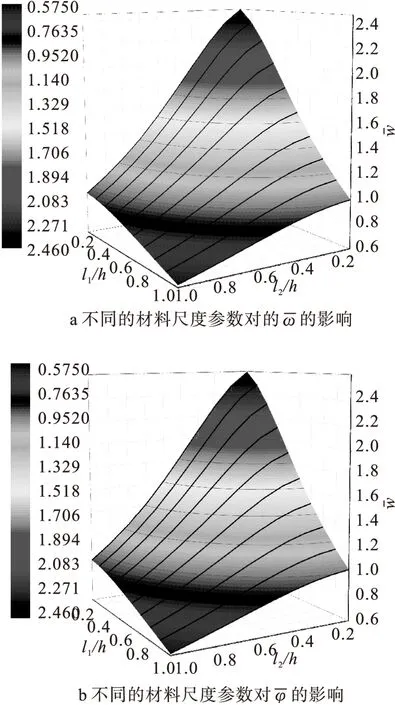
图3 不同的材料尺度参数对无量纲和的影响
4.3 功能梯度变化指数r的影响
5 结论
(1)基于新修正偶应力理论,本文首次建立了特殊的正交各向异性功能梯度压电微板的弯曲模型。模型中弥补了修正偶应力理论只适用于各向同性压电材料的这一不足,通过引入两个正交方向上的材料尺度参数从而能够分别描述两个不同方向上的尺度效应。
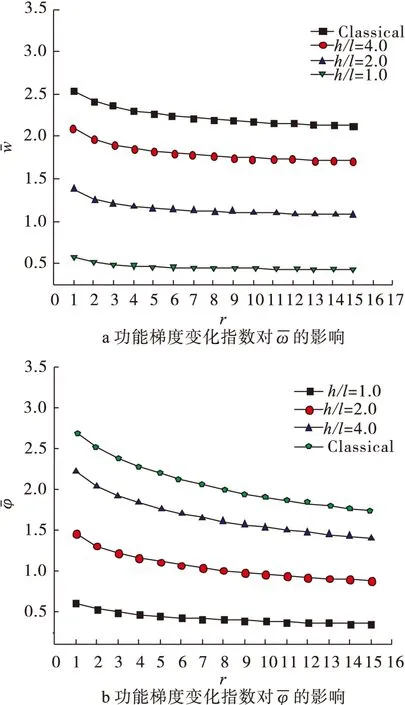
图4 功能梯度变化指数对无量纲和的影响
(3)功能梯度变化指数对压电板的弯曲挠度和电势能也有一定的影响。功能梯度变化指数主要通过影响材料属性在结构厚度方向上的分布形式,从而影响结构的力学性能。
