“先猜后证”在解几探究性问题中的应用
2018-07-30福建省龙岩一中364000方秦金
福建省龙岩一中 (364000) 方秦金
“猜想”是合情推理,“证明”是演绎推理,“先猜后证”就是先用合情推理的方法得到一个似真的结果,再用演绎推理证明这个结论的正确性.本文举例说明“先猜后证”在解几探究性问题中的应用,供参考.
1.应用“先猜后证”探究直线与圆的位置关系
例1 (2014年北京高考理科卷第19题)已知椭圆C:x2+2y2=4.
(Ⅰ)求椭圆C的离心率;
(Ⅱ)设O为原点,若点A在椭圆C上,点B在直线y=2上,且OA⊥OB,试判断直线AB与圆x2+y2=2的位置关系,并证明你的结论.
我们先看命题者给出的解答.
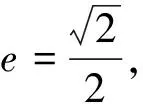
(Ⅱ)直线AB与圆x2+y2=2相切.证明如下:



2.应用“先猜后证”探究定点问题

图1

(Ⅰ)求椭圆E的方程;
(Ⅱ)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.

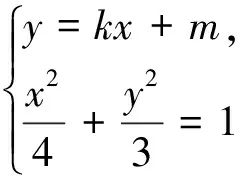

下面证明M(1,0)就是满足条件的点.

评析:假设存在满足条件的点M,我们通过取k,m的特殊值得出M的坐标,再给以一般化的证明,这是“先猜后证”方法的应用.
3.应用“先猜后证”探究点与圆的位置关系

(Ⅰ)求椭圆E的方程;
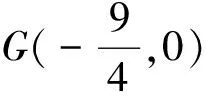
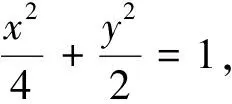

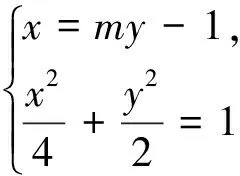
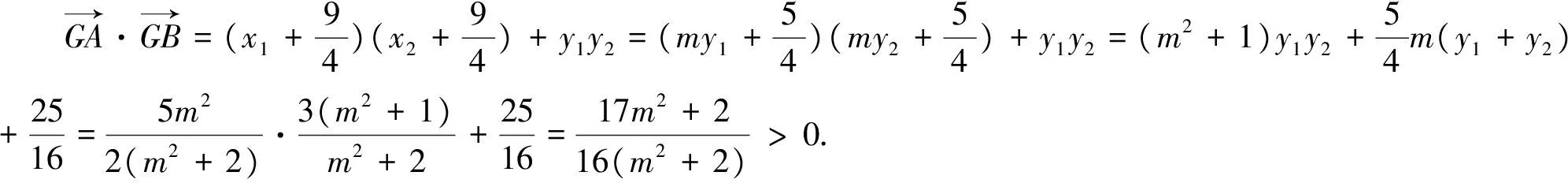

我们由特殊情形得到点G与以AB为直径的圆的位置关系,“先猜”为“后证”指引了明确的方向.
4.应用“先猜后证”探究定值问题
例4 已知动圆P与圆F1:(x+3)2+y2=81和圆F2:(x-3)2+y2=1都相内切,即圆心P的轨迹为曲线C;设Q为曲线C上的一个不在x轴上的动点,O为坐标原点,过点F2作OQ的平行线交曲线C于M,N两个不同的点.
(Ⅰ)求曲线C的方程;
(Ⅱ)试探究|MN|和|OQ|2的比值能否为一个常数?若能,求出这个常数;若不能,请说明理由.
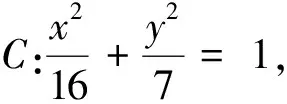
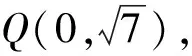



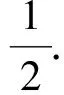
评析:如果没有用特值的方法得出一个可能的结果,则证明的方向是不确定的,繁杂的字母运算也令人望而却步.“先猜后证”鼓舞了解题的信心.
回顾以上四个例子,“先猜后证”可为解几探究性问题指引方向,从而化繁为简,也体现了数学的简洁美.
