刍议数学课堂中学生思维能力的培养

福建省三明市宁化县东风小学 陈雪花

《数学课程标准》明确指出：数学是人类文化的重要组成部分。数学文化对于推动人类进步的意义集中体现于数学思维能力上，因而数学思维能力的培养就成为数学课堂的核心目标。良好的思维能力能够提升学生观察参与社会的能力，增强感悟明辨是非的能力，更好地体验数学学科的无穷奥妙。那么，如何在小学数学课堂中培养好学生的思维能力呢？下面是笔者在教学实践中的一些尝试与思考。

一、创设问题情境，点燃思维火花

没有问题就没有思维，或者说没有有效的思维。因此，在数学教学过程中，教师要创设学生喜欢的、符合他们年龄特征的问题情境，激发他们的学习兴趣和求知欲望，变“要我学”为“我要学”，使学生真正成为学习的主人，从而点燃思维的火花。

例如：教学人教版六年级上册《总量可用“1”表示的工程问题》时，教者结合当代建设美丽新农村的话题,给学生展示了一组教者老家美丽乡村公路建设的幻灯片。同学们像看电影一样，目不转睛，聚精会神，因为他们没想到在数学课上也能看风景。接着出示了我们学校小溪边破破烂烂的道路，同学们异口同声地说道：“我们也要修路。”顺理成章地引入了本节课。“这条公路长1500米，如果甲队单独修，6天修完，如果乙队单独修，10天修完，如果你是负责人，在保质保量的情况下，你会选哪个施工队呢？”

生1： 乙队。

生2： 甲队，因为甲队用的时间少，修得更快。

师：如果要修得更快些，还可以怎样修呢？

齐答： 两队合修。

再出示：“一条公路，如果甲队单独修，6天修完，如果乙队单独修，10天修完”。

师：与上题有什么不同的地方？

生： 总长不知道。

师：怎么办？

生： 可以假设成任何一个具体量，也可以假设成“1”来列式计算。

教者在整个教学过程中设计了一个又一个的数学问题情境，环环相扣，层层引入。同学们跃跃欲试,课堂气氛非常浓，学生在一个很轻松的环境中理解并掌握了本节课的教学内容。

二、给予足够的时空，培养思维意识

《课标》明确指出：在数学活动中，教师应给学生充分从事活动的机会，留给学生独立思考的时间和空间。在课堂教学中，教师应尽量克服一问一答、全体齐答的现象，而应引导学生采取先独立自主探究，再小组合作学习的形式，培养学生的思维意识，体验到动脑、动手、动眼、动口带来的惊喜。

例如在求如图所示的阴影部分的周长时，先让学生观察周长是指哪部分，再让学生摸一摸，明确阴影部分周长等于大圆周长的一半加上两个小圆周长的一半后，开始让学生动手计算： 大圆周长的一半： 3.14×（5+5）÷2=15.7（厘米），两个小圆周长的一半之和：3.14 ×5÷2+3.14×5÷2=15.7（厘米），阴影部分周长等于：15.7+15.7=31.4（厘米）。这时有些学生发现大圆周长的一半与两个小圆周长一半的和相同，都是15.7厘米，那么阴影部分的周长也可以用圆周长的一半乘2，即3.1×（5+5）÷2×2=31.4（厘米）。平时爱思考的张凯马上补充道：“其实还可以更简单些，只要一步就能完成，因为乘2 和除以2可以抵消，所以列式成3.14×10=31.4（厘米）。”顿时全体同学惊呆了，太神奇了！如此复杂的列式和计算怎么可以这么简单啊？在这种思维的助推下，同学们继续补充道，只要类似这些求阴影部分的周长，都可以用最后一种方法。如下图：

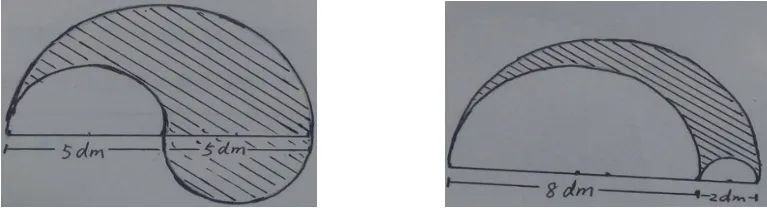
本节课老师给予学生足够的时空，学生通过自己的努力一步一步地归纳总结出最简便的计算方法，他们在参与活动中亲身感受到成功和创新的喜悦。

三、利用已有知识，开启思维大门

学生新知识的学习是建立在已有知识的基础上的，因此教师教学应该从学生的认知发展水平和已有的经验下手，注重启发式教学和因材施教，使学生理解和掌握基本的数学知识与技能，才能更好地开启他们的思维大门，获得许多课堂上意外的生成。例如：在教学人教版五年级下册“通分”第一课时时，有这样一个例题：“陆地面积约占的陆地多还是海洋多吗？”

在这个问题的解决中，同学们表现出强烈的学习欲望，因为他们能利用直接看图、分数单位、分数的意义、分别与和1比较等学过的知识来解决新问题，不同层次的学生的思维能力得到不同的发展，每一个学生的思维大门都被打开，获得一定的成就感。

四、鼓励大胆创新，铺设思维之路.

数学教学的关键在于我们教师要有意识地培养学生的思维能力,引导学生走上思维之路，那就要求我们的学生除了掌握一定的数学知识和技能外,还必须有创新能力。课堂教学作为培养学生创新能力的主渠道，应该相信学生，放手让他们敢于尝试，敢于大胆解决问题。

如在教学五年级下册时一道练习题：“一根铁丝刚好可以围成一个长5分米，宽4分米，高3分米的长方体框架，如果把它围成一个最大的正方体，这个正方体的棱长是多少？”通常同学们会先算出长方体的棱长总和“（5+4+3）×4=48（分米）”,再用48÷12=4（分米），求出正方体的棱长，当做到这里时大家都觉得完成任务了，这时有位学生举手了，他说：“（5+4+3）÷3=4（分米）,理由是正方体是长、宽和高都相等的长方体。”这位学生能够利用长方体和正方体特征方面的联系,脱离常规思路,用自己独特的方法解决问题,这就是一种创新思维,而只有这种思维之路才能使学生走得更稳、更远。

五、实现主动学习，形成思维品格

学生的学习应当是一个生动活泼的、主动的和富有个性的过程，同时教师还要注重培养学生良好的学习习惯,进行有序思维,从而形成思维品格。

如学习完百分数的意义后，利用其意义解决问题时，教师出示了这样一道题：“电视机厂原计划生产电视机20万台，实际生产了25万台。（1）实际是计划的百分之几？（2）计划是实际的百分之几？（3）实际比计划多百分之几？计划比实际少百分之几？通过练习，学生主动发现它们都是求一个数是另一个的百分之几的问题,只要找到一个数和另一个数再相除就可以了，学生会感受到良好的思维习惯是有章法的，不是乱来的，就如上面通过对比类化——归纳小结得出了它们的解题共同点。数学学习不是死记硬背，更不是生搬硬套，而是一种思维和方法，思维方法的掌握将使人们受益一生。

总之，培养学生的数学思维能力是我们数学教师的首要任务，也是教学的核心目标。因此在课堂教学中，我们应以学生为主体，根据学生已有知识和实际情况创设问题情境，引导学生独立思考，勇于探索，大胆创新。在数学课堂中，努力使学生在数学活动中开拓思维，感受数学学习的乐趣和价值，真正做到有效地提升学生的思维能力。