在数学活动中积累活动经验

福建省泉州市永春县岵山中心小学 陈燕虹

《义务教育数学课程标准（2011年版）》增加了基本的数学思想方法和基本的数学活动经验。数学活动经验是一种过程性知识，是深入理解和掌握数学，灵活地运用数学知识解决问题所不可缺少的。那么怎样引领学生在数学活动中更好地积累数学活动经验呢？我结合平时的教学谈几点看法：

一、搭建操作平台，在体验中积累经验

动手实践操作的重要性不言而喻。上课前，师生共同准备所需要的教具、学具等材料工具，一起搭建操作实践的平台；上课时，引导学生通过摆一摆、剪一剪、摸一摸、画一画、试一试、找一找等多种活动，让学生亲身经历、深刻体验，切实感悟。让学生充分地经历和体验，是学生积累活动经验的“前奏曲”，数学活动经验需要在“做”的过程和“思考”的过程中积淀。

案例一：北师大版三年上册“什么是周长”。

1.摸一摸：刚才我们看了小蚂蚁绕着树叶边线跑，你们能否像这样摸一摸树叶的边线？

2.描一描：你能不能把树叶一周的痕迹留下来？边描边说：我从哪一点开始描，描到哪里就结束了。

看来不管你们怎么描，大家都是沿树叶的边线描了一周。

3.找一找：还有什么图形或物体的表面也有一周？我们就地取材，和同桌一起分享你的发现。

4.画一画：选择信封中一个你喜欢的图形，用彩笔将蜗牛走的路线画出来。

5.揭示周长的概念。

正如弗赖登塔尔所言：数学学习活动如同游泳、骑车，如果不去亲力亲为，单单只是看书、听讲、看别人演示是不可能学得来的。数学经验的积累离不开学生的亲身参与，体验感悟，达到内化，以期能自主建构知识体系，从而灵活应用所学的知识。老师要为学生搭好这个脚手架，正如吴正宪老师说的：孩子们的指尖上闪烁着智慧，任何高明的教师都代替不了学生的操作。学生因做而思，因思而悟，因悟而创。

二、创设交流机会，在分类中积累经验

学生在参与数学活动时，老师要留足时间，让学生充分地合作交流，产生思维碰撞，更好地反思领悟自己的学习过程，这样有利于各自经验的交流与融合，达到个人经验的优化与内化，以期更有效地积累分类的活动经验。

案例二：北师大版一年下册“分扣子”。

1．尝试操作，感知分类

出示一堆不同的扣子，要求分成两类，再汇报交流。

生1：按形状分，分成圆形和正方形。

生2：按扣眼数分，分成了两个扣眼和四个扣眼。

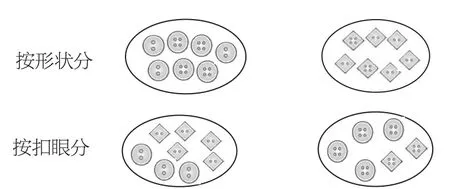
2．发现问题，交流反思

（1）发现问题：同样的扣子，分类结果不一样。

（2）交流反思：为什么同样的扣子分类的结果会不一样？

在动手操作时，在直观的实物展示中，通过观察发现：分类标准可以不同；不同的分类标准分得的结果也不相同。结合动手操作、探究交流，学生更好地把握了图形的特征，进而抽象出多个图形的共性，帮助学生积累分类的活动经验。

3．观察讨论，深刻体验

观察、讨论：每种分法还能继续往下分吗？

生3：我们发现还可以继续往下分：形状相同的就按扣眼数再接着分，分成了两个扣眼数的和四个扣眼数的；扣眼数相同的按形状再继续分类，分成了圆形和正方形。

4．交流分享，溯本求源

师：千金难买回头看，我们回头看一下刚才是怎么分扣子的？我们首先按什么标准分类？怎样分？

师：表达得有条有理，两种分法各分了几次？最后分成了几类？

生：两种分法各分了2次，最后分成了4类。

师：这两种分类方法有什么不一样的地方？

生：一种是先按形状分成两类，再按扣眼数继续往下分；另一种则是先按扣眼数分成两类，再按形状接着分。

师：这两种分法有什么一样的地方？

生：都是分了再分，结果都是一样的，都分成了四类。

小结：这两种分法看似不同，却有着相同之处——分了再分，分得的结果一样。

学生亲自经历了这样两次的分类过程，从动手操作到分析，从分析到反思，在交流分享中感受到确定分类标准的必要性。这对大部分学生的顿悟、理解、掌握起着至关重要的作用，交流分享是为了“动”而后的“静”，再由“静”转向“互动”，建构认知，积累了观察分类的数学活动经验。

三、聚焦数学本质，在建模中积累经验

聚焦活动中的数学知识本质，对生活中的具体问题进行提炼、抽象，建立初步的数学模型，在深入探究中积累建立模型的活动经验。

案例三：北师大版五年上册“小数除法”。

创设情境：妈妈付了100元，买4把雨伞，找回3元，每把雨伞需要多少钱？经过计算：97÷4=24（元）……1（元）。

展示学生的作品，有通过文字、图画等多种形式，理解怎样把剩余的1元平均分成4份……

学生的质疑：你怎么会想到1元=100分，我都没想到？

生1:100分可以平均分成4份。

师：这个经验值得推广，把1元换成100分，就可以再继续分。

生3问生4：为什么1元分成10角？怎么想到的？我怎么没想到，剩下2角不够分，不换不行吗？

生4：1元不能平均分成4份，得再缩小一个单位。1元不够除以4，变成10角，我们就活了。

师：剩2角不够分，怎么办？

生1：2角=20分。

生2：为什么想到2角=20分？

生1：因为要把2角平均分成4份，不够分，就想到2角=20分。20分，平均分成4份，可以分了。

……

这样的层层递进，由元、角、分，到米、分米这样的数学模型，回归到计数单位，回归到数学本质，把活动的“针”扎到数学活动经验的“根”上，扎到数学的魂上，这样的抓大放小，把碉堡解决，则一通百通。

数学活动经验的积累，需要在数学活动的“体验”“交流” 中得以进行；数学活动经验的积累，是在聚焦数学知识本质、构建数学模型中逐渐提升的。