49MnVS3非调质钢的两种轧制力模型对比
2018-07-27,,,,,
, , , , ,
(西安建筑科技大学冶金工程学院,西安 710055)
0 引 言
随着计算机技术在热轧生产过程中的广泛应用,现代化轧钢的生产流程已向自动化、高速化和优质化方向发展[1]。在棒线材轧制过程中,变形抗力和轧制力的准确计算对于保证轧制规程的顺利进行是非常重要的[2]。轧制力是指轧件变形时作用于轧辊上总压力的垂直分量,研究轧制过程中接触弧上单位轧制压力的分布规律对准确确定轧制力有重大意义。正确预测轧制力的大小不仅可以合理使用设备和安排轧制规程,还能减少设备损耗和节约生产成本,而平均单位轧制压力与金属的变形抗力直接相关[3-5]。棒线材生产过程中各环节的温度变化、轧制工艺的制定以及产品质量的控制等,都将直接影响最终轧制工艺的稳定性和生产的精确性,并需要精确的数学模型对轧制过程进行控制,从而获得更高精度的产品[6-8]。此外,金属的热变形抗力对于轧制工艺的制定和轧机设备的选择是必不可少的[9-10]。因此,建立能正确反映金属材料力学性能参数与热变形工艺参数关系的数学模型,可实现轧制过程的计算机模拟,从而达到优化热轧工艺和进一步提高材料力学性能的目的。热轧轧制力计算模型主要有艾克隆德模型、周纪华-管克智变形抗力模型等。周纪华-管克智变形抗力模型通过拟合的轧制力计算出单位轧制压力,这需要大量的试验数据进行拟合;而艾克隆德模型以理论和试验数据为基础建立了计算平均单位轧制压力的半经验公式[2,7,11-12]。曲轴用49MnVS3钢是一种中碳、钒微合金化含硫非调质钢,具有高韧性、易切削、力学性能与中碳调质钢的相当或更优异等特点,同时其生产中无需淬火、回火、校直、消除应力回火等工序,可节约能源,有“绿色钢铁”之称[13-15]。为了给49MnVS3非调质钢的轧制工艺设计提供准确的轧制力计算方法,作者分别采用周纪华-管克智变形抗力模型和艾克隆德模型计算了该钢在棒材轧制过程中各机组不同道次的平均单位轧制压力,并进行了比较。
1 试样制备与试验方法
试验材料为49MnVS3非调质钢,由西宁特殊钢股份有限公司提供,其化学成分见表1。将试验钢加工成尺寸为φ10 mm×15 mm的试样,在Gleeble-3500型热模拟试验机上进行单道次热压缩试验,变形温度为750,800,850,900,950,1 000 ℃,应变速率分别为0.1,1,10,50 s-1,变形量为60%(真应变为0.92),变形结束后立即水冷至室温。在试验过程中同步采集真应力和真应变数据,得到真应力-真应变曲线。
试验钢在棒材连轧生产线上轧制时19个机架的孔型系统和轧制工艺参数见表2。

表1 49MnVS3非调质钢的化学成分(质量分数)Tab.1 Chemical composition of 49MnVS3 non-quenchedand tempered steel (mass) %

表2 棒材连轧生产线的孔型系统和试验钢的轧制工艺参数Tab.2 Pass sequence of continuous rod production line androlling process parameters of tested steel
2 试验结果与讨论
2.1 真应力-真应变曲线
由图1可知:在不同变形温度下试验钢的真应力均随着应变的增加先增大后趋于稳定;当应变速率一定时,真应力随着变形温度的升高而降低;当变形温度一定时,真应力随应变速率的增加而增大;在变形温度为750 ℃,应变速率为50 s-1条件下,试验钢的真应力峰值达到400 MPa左右。
2.2 周纪华-管克智变形抗力模型的建立
周纪华-管克智变形抗力模型的计算公式为
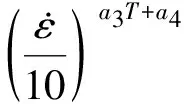
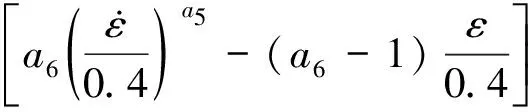
(1)
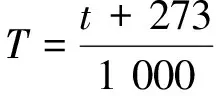
(2)
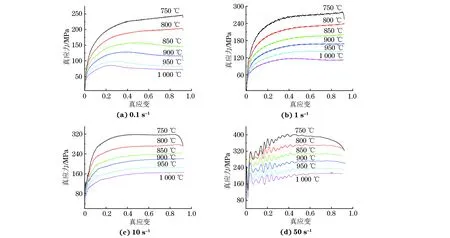
图1 不同变形温度和应变速率下试验钢的真应力-真应变曲线Fig.1 Ture stress-true strain curves of the tested steel at different deformation temperatures and strain rates
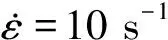
用Origin软件对图1中不同变形温度和应变速率下的真应力与真应变进行非线性回归分析,拟合得到试验钢变形抗力模型中的回归系数和基准变形抗力,如表3所示。

表3 拟合得到试验钢周纪华-管克智变形抗力模型的回归系数和基准变形抗力Tab.3 Regression coefficient and reference deformation resistance of Zhou Jihua-Guan Kezhi deformation resistancemodel of the tested steel after fitting
将回归系数和σ0代入式(1)得到:
σ=157exp(-2.860 25T+

(3)
2.3 平均单位轧制压力模型的对比
以孔型K5、K4为例,根据表2的孔型系统和轧制工艺参数计算平均单位轧制压力。
基于艾克隆德模型,平均单位轧制压力的计算公式[7]为
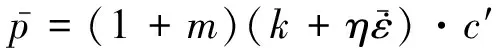
(4)
c′=0.968 2+0.006 56v
(5)
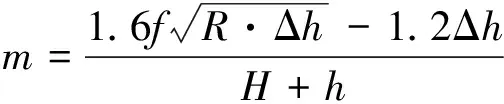
(6)
k=10×(14-0.01t1)×
[1.4+w(C)+w(Mn)+w(Cr)]
(7)
f=a(1.05-0.000 5t1)
(8)
η=0.1(14-0.01t1)c
(9)


表4 轧制速度影响系数Tab.4 Influence coefficient for rolling speed
将表2和表4中的数据代入式(4)~式(9),得出K5孔入K4孔时的基于艾克隆德模型的平均单位轧制压力为221.31 MPa,采用同样的计算方法得到其他道次的平均单位轧制压力列于表5中。
基于周纪华-管克智变形抗力模型,平均单位轧制压力的计算公式[2]为
(10)
式中:nσ为应力状态影响系数。
(11)

(12)
ak=Bk/H
(13)
A=D*/H
(14)
式中:q为变形区形状参数;ak为孔型轴比;A为轧辊转换直径,mm;Bk为轧辊宽度,mm;D*为轧辊孔型槽底直径,mm。
将表2中的数据代入式(11)~式(14),得到nσ为1.54,然后代入式(10)求得K5孔入K4孔时的基于周纪华-管克智变形抗力模型的平均单位轧制压力为178.54 MPa,采用同样的计算方法得到其他道次的平均单位轧制压力如表5所示。
由图2和表5可知:随着轧制道次的增加,即应变的增加,基于艾克隆德模型和周纪华-管克智变形抗力模型计算得到的平均单位轧制压力均增大;基于艾克隆德模型得到的平均单位轧制压力曲线波动较小,而基于周纪华-管克智变形抗力模型,通过热模拟试验结果拟合得到的平均单位轧制压力曲线波动较大,这是由于变形程度对基于周纪华-管克智变形抗力模型得到的轧制力的影响比较大而造成的;在低应变速率(粗轧、中轧与预精轧阶段)下,基于艾克隆德模型计算得到的平均单位轧制压力较大,而在高应变速率(精轧阶段)下,基于周纪华-管克智变形抗力模型计算得到的平均单位轧制压力较大,这主要与高应变速率引起的形变强化、温升效应及动态再结晶等因素有关。
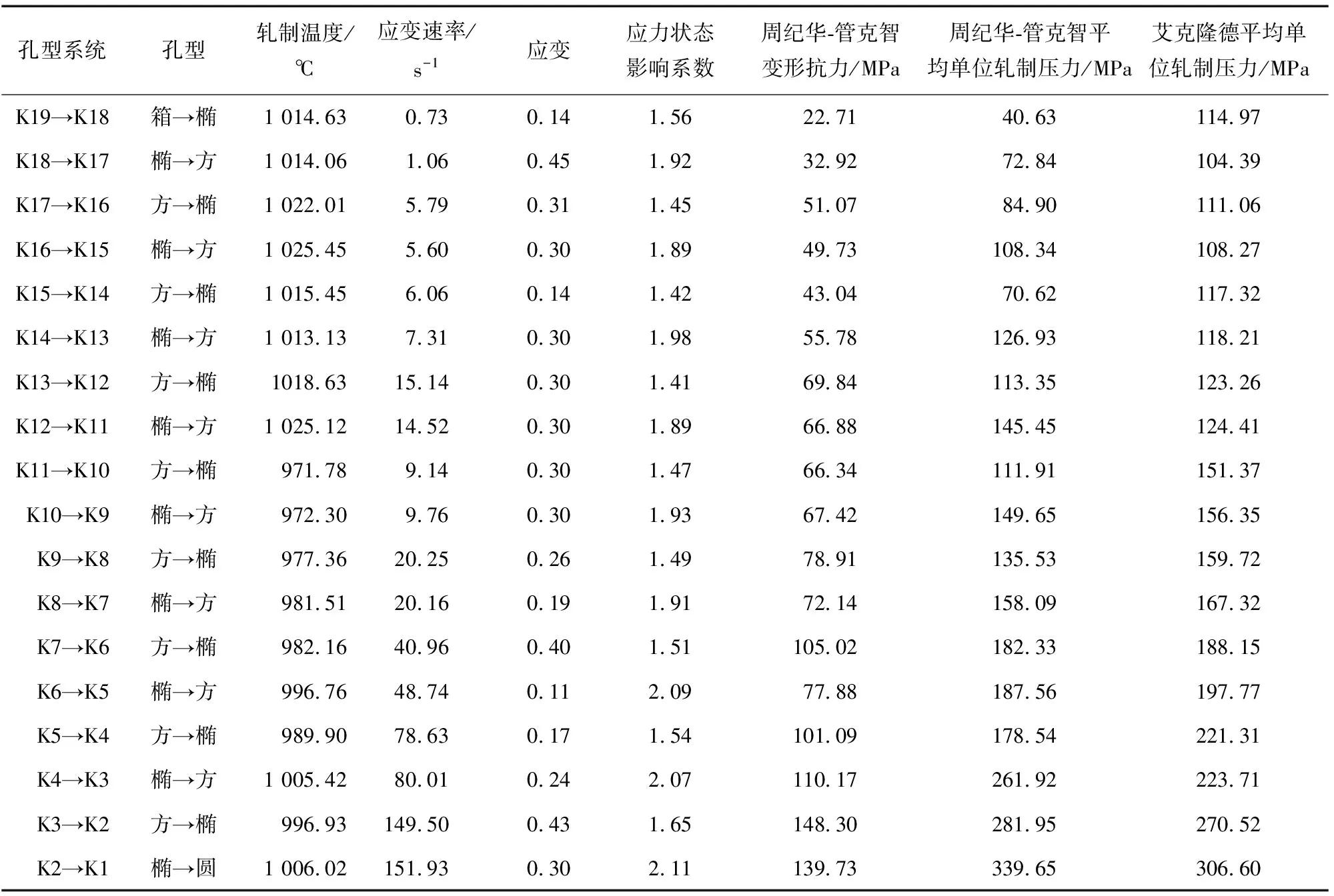
表5 基于两种模型计算得到的平均单位轧制压力Tab.5 Calculated average unit rolling prossures on basis of two models

图2 基于两种模型得到的平均单位轧制压力的对比Fig.2 Comparison of average unit rolling forces obtained on basis of two models
基于周纪华-管克智变形抗力模型计算平均单位轧制压力时,需要借助热模拟试验得到的数据,因此不同轧制道次的变形量对其影响很大,该模型接近于实际生产情况,适用于控制模型;而艾克隆德模型通过材料的化学成分和轧制工艺参数来计算平均单位轧制压力,因此其在实际设计中的应用更加广泛,该模型适用于轧制工艺设计。
3 结 论
(1) 随着轧制道次的增加,即应变的增加,基于艾克隆德模型和周纪华-管克智变形抗力模型计算得到的平均单位轧制压力均增大;基于艾克隆德模型得到的平均单位轧制压力曲线波动较小,而基于周纪华-管克智变形抗力模型的波动则较大;在低应变速率(粗轧、中轧与预精轧阶段)下,基于艾克隆德模型计算得到的平均单位轧制压力较大,而在高应变速率(精轧阶段)下,基于周纪华-管克智变形抗力模型计算得到的平均单位轧制压力较大。
(2) 基于周纪华-管克智变形抗力模型计算轧制力时,需要借助热模拟试验得到的数据,该模型适用于控制模型;艾克隆德模型只需使用化学成分和轧制工艺参数即可计算平均单位轧制压力,应用更广泛,该模型适用于轧制工艺设计。
