2219铝合金热压缩时的流变应力本构方程

，，，，

(中南大学1.轻合金研究院，2.高性能复杂制造国家重点实验室，长沙 410083)

0 引 言

2219铝合金属于Al-Cu-Mn 系可热处理强化合金，具有良好的低温和高温力学性能、断裂韧性、焊接性能以及抗应力腐蚀能力等，广泛应用于航空、航天等领域[1]，主要用于制造火箭箭体结构件和燃料贮箱封头件。目前，我国主要采取冷旋压技术对火箭燃料贮箱封头进行整体加工成形，但成形后封头容易出现起皱、开裂等变形不协调的现象。热旋压加工技术在降低材料变形抗力和提高材料塑性等方面具有独特的优势[2]，因此有必要研发制造大型铝合金封头件的热旋压加工工艺。

目前，国内外学者对2219铝合金的研究主要集中在搅拌摩擦焊[3-4]、热处理后的机械加工性能[5]、稳态蠕变本构方程[6]等方面，对其热变形时的流变应力本构方程研究较少。当热旋压温度超过350 ℃时，铝合金板材软化太严重，不利于对其进行加工。因此，作者对O态2219铝合金在350 ℃及以下温度进行高温压缩试验，研究了该铝合金在不同应变速率和变形温度下的流变行为，建立了热压缩时的流变应力本构方程，为制定2219铝合金的热旋压加工工艺提供理论依据。

1 试样制备与试验方法

试验材料为O态2219铝合金板，由广西南南铝加工有限公司提供，其化学成分如表1所示。在铝合金板上截取尺寸为φ7 mm×10.5 mm的圆柱体试样，在Gleeble-3180型热模拟试验机上进行单道次热压缩试验。试验前将热电偶焊接在试样侧面测试样的温度，以确保其温度在试验过程中保持不变；以5 ℃·s-1的升温速率将试样加热到变形温度(200，250，300，350 ℃)，保温5 min后，分别以0.1，1.0，10.0 s-1的应变速率进行压缩变形，总变形量为30%，总应变为0.36，压缩变形结束后立即水冷到室温。

表1 2219铝合金的化学成分(质量分数)Tab.1 Chemical composition of 2219 aluminumalloy (mass) %

2 试验结果与讨论

由图1可以看出：当应变速率相同时，2219铝合金的流变应力随着变形温度的升高而减小，同时该铝合金的压缩屈服强度和抗压强度降低，这是因为变形温度越高，铝合金抵抗变形的能力越弱；当变形温度相同时，2219铝合金的流变应力随着应变速率的增大而增大，同时该铝合金的压缩屈服强度和抗压强度也升高。在较大的应变速率下，晶粒无法在短时间内滑移，只能在原地做弹性摆动，且其摆动幅度随应变速率的增大而增大[7]，而摆动幅度与应力、屈服强度和抗压强度成正比；同时应变速率的增大使应变时间缩短，材料来不及软化，从而产生应变速率硬化效应；另外，随着压缩的不断进行，2219铝合金产生应变硬化效应：因此，流变应力、屈服强度、抗压强度均随应变速率的增大而增大。

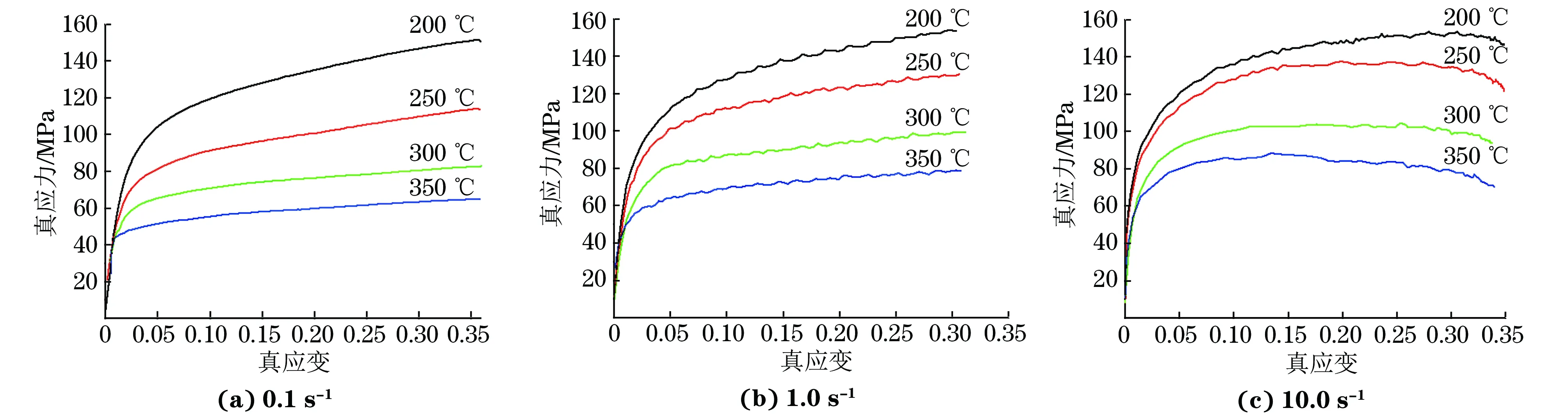
图1 不同应变速率和变形温度下2219铝合金的真应力-真应变曲线Fig.1 Ture stress-true strain curves of 2219 aluminium alloy at different strain rates and deformation temperatures

3 流变应力本构方程的建立

由于2219铝合金在热压缩过程中存在应变硬化和应变速率硬化现象，因此选用Fields-Backofen方程来描述其流变行为，其表达式为

(1)

式(1)中n的大小表明材料均匀变形能力的强弱，n越大，则材料的硬化效应越明显，成形极限越高。对式(1)两边分别取自然对数，得到

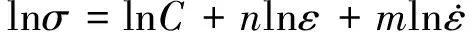
(2)

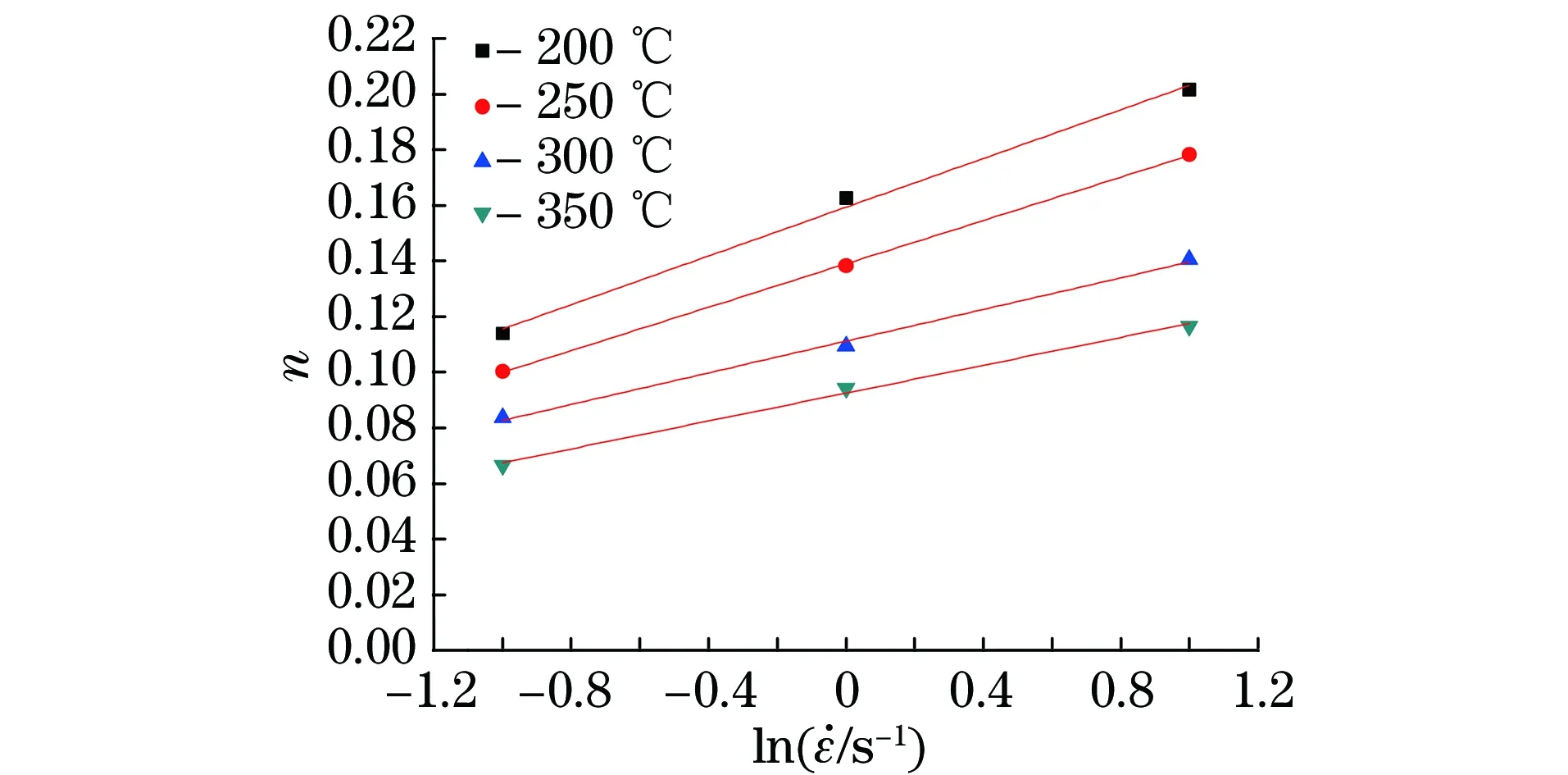
图2 不同变形温度下n与的拟合曲线Fig.2 Fitting curves of n vs at different deformation temperatures

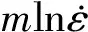
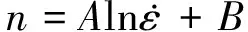
(3)

式中：A为应变速率对n的影响系数；B为变形温度对n的影响系数。A，B的拟合结果如表2所示。

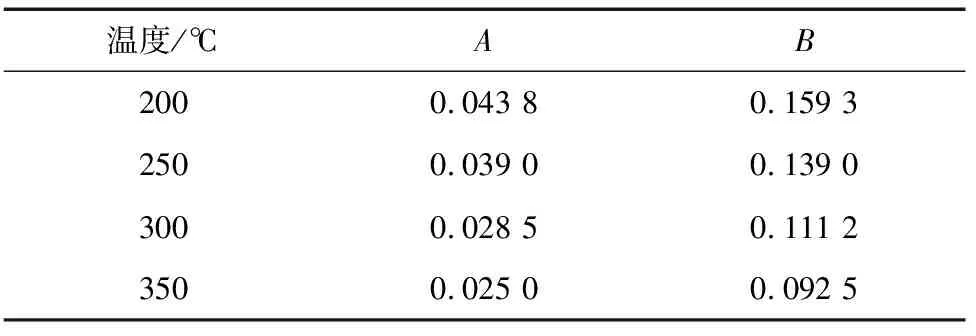
表2 不同变形温度下A，B的拟合结果Tab.2 Fitting results of A and B at differentdeformation temperatures

由表2可以看出：不同变形温度下的A相差不大，这表明应变速率对n的影响较小，因此A可取不同变形温度下的平均值，即0.034。用Origin软件拟合可知，B与温度T呈近似线性关系，关系式为

B=-4.568e-4T+0.251

(4)

将A,B代入式(3),得到参数n的表达式为

(5)

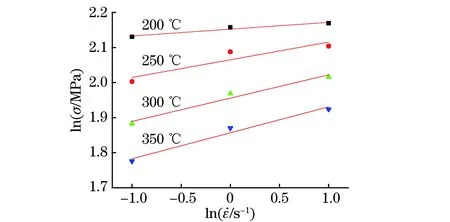
图3 不同变形温度下lnσ与的拟合曲线Fig.3 Fitting curves of lnσ vs at different deformation temperatures

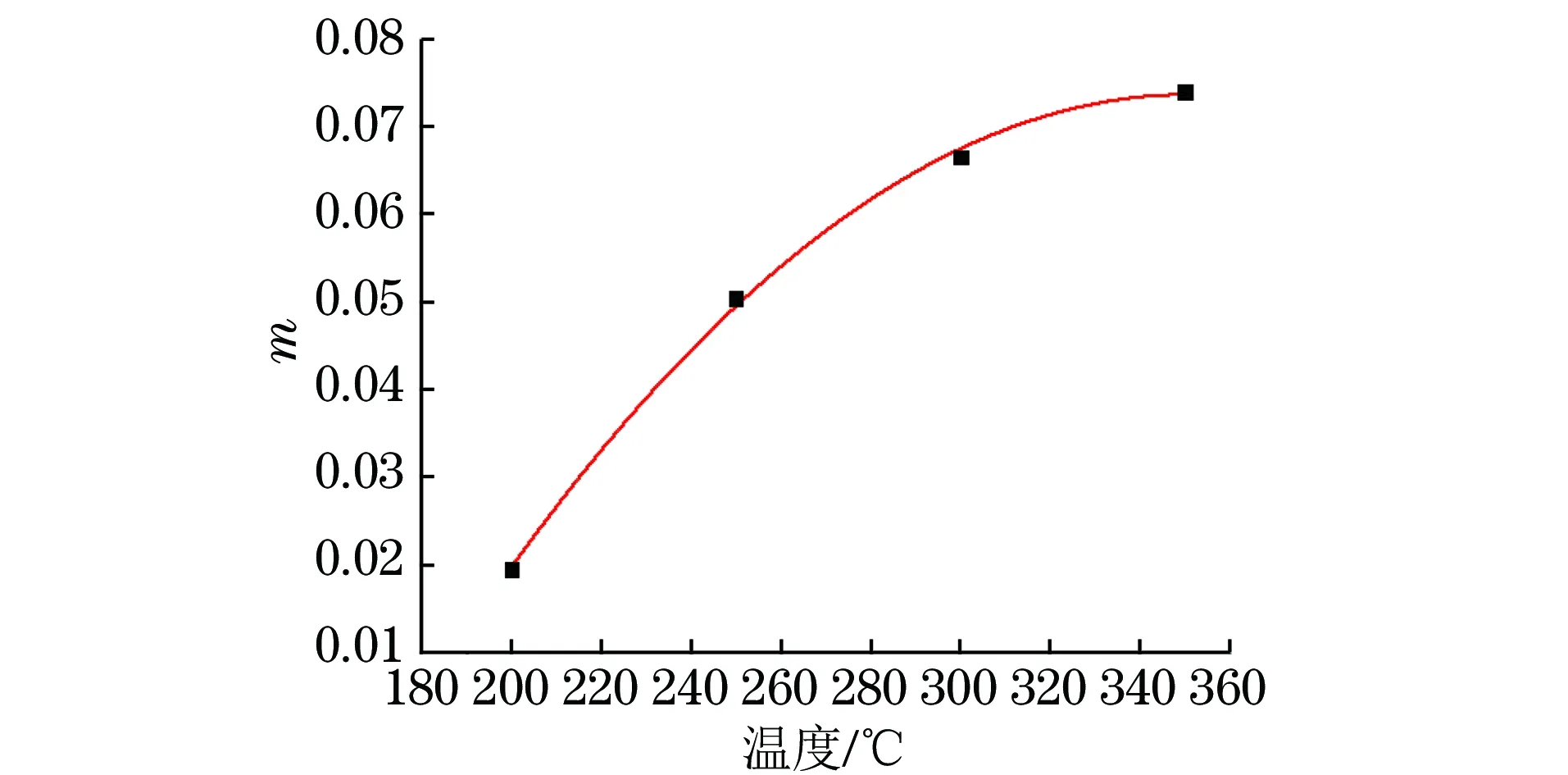
图4 m和变形温度间的关系曲线Fig.4 Relation curve of m vs deformation temperature

由图4可以看出，m与变形温度基本呈二次函数的变化规律，拟合得到m的表达式为

m=-2.35e-6T2+0.001 65T-0.216 57

(6)

由式(1)可推导出C的表达式为

(7)

(8)

式中：C1为应变速率对C的影响系数；C2为变形温度对C的影响系数。

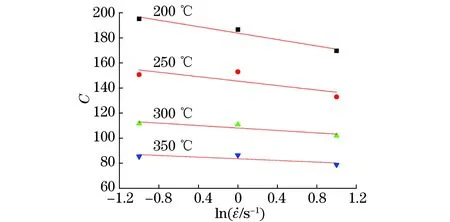
图5 不同变形温度下C和的拟合曲线Fig.5 Fitting curves of C vs at different deformation temperatures

拟合得到的C1，C2如表3所示。由表3可以看出，不同变形温度下的C1相差较小。为简化模型，C1取不同变形温度下的平均值，即-7.48。用Origin软件拟合得到C2与变形温度基本呈线性关系，可以得到C2的表达式为

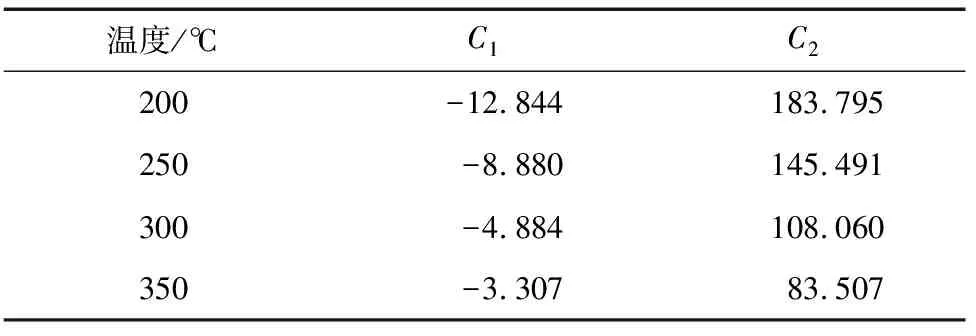
C2=-0.676 59T+316.276

综上所述，2219铝合金热压缩时的Fields-Backofen本构方程的3个参数的表达式分别为

(10)

m=-2.35e-6T2+0.001 65T-0.216 57

(11)

(12)

4 本构模型的验证

将拟合得到的相关参数代入Fields-Backofen本构方程，计算得到应变速率分别为0.1，1.0，10.0 s-1和变形温度分别为200，250，300，350 ℃下2219铝合金的真应力-真应变曲线。由图6可以看出，通过本构方程计算得到的应力的变化规律与试验得到的相同。

图6 计算得到2219铝合金在不同应变速率和变形温度下的真应力-真应变曲线Fig.6 Calculated true stress-true strain curves of 2219 aluminium alloy at different strain rates and deformation temperatures

为进一步验证2219铝合金热压缩本构方程的准确性，将试验测得的应变速率为0.5 s-1、不同温度下的真应力-真应变曲线与计算所得曲线进行对比。由图7可以看出，应力计算值与试验值的相对误差小于5%，这说明该本构方程具有较高的准确性。

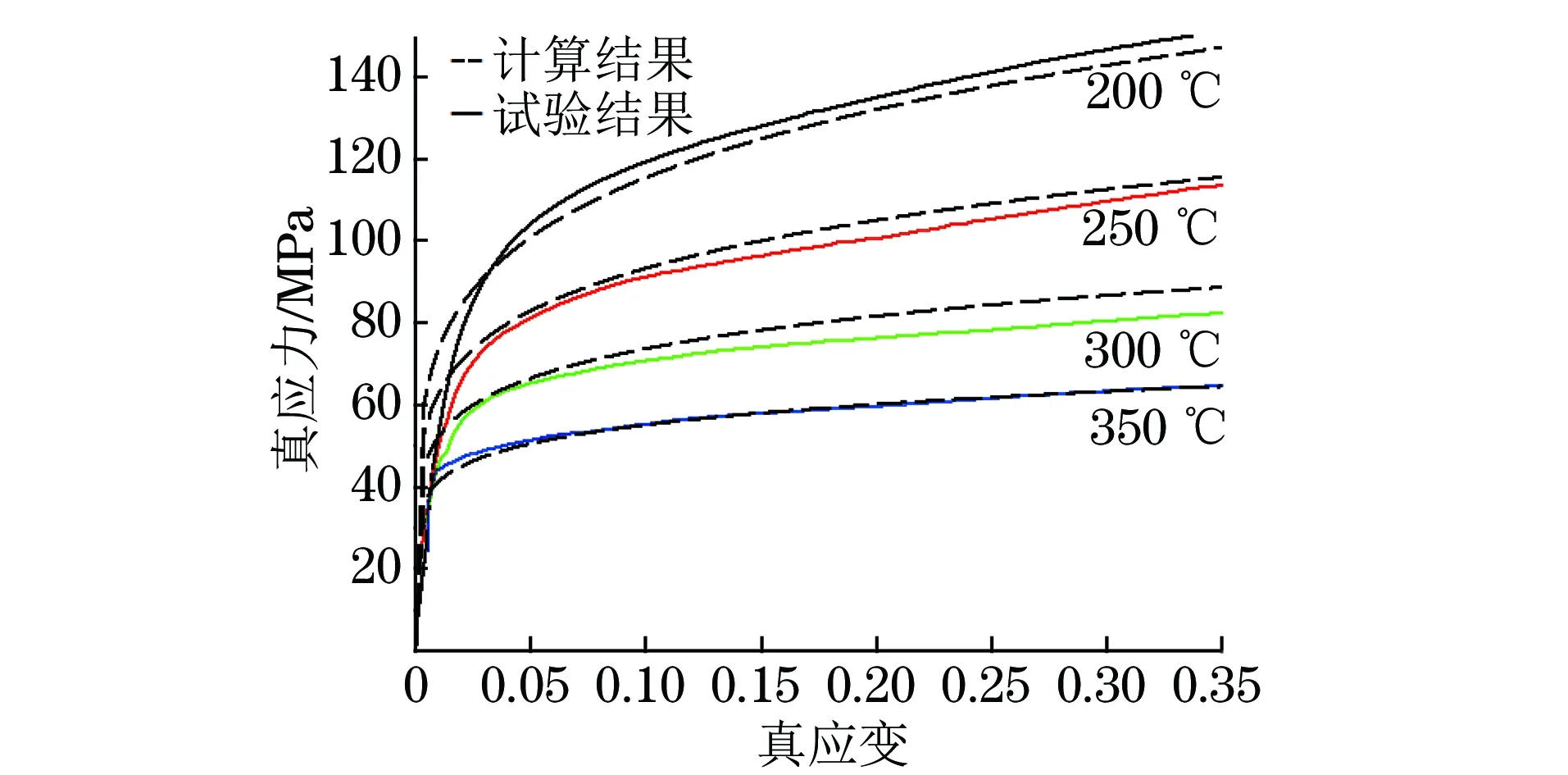
图7 2219铝合金在应变速率0.5 s-1和不同变形温度下真应力-真应变曲线的计算结果和试验结果的对比Fig.7 Comparison of calculated results and experimental results of true stress-true strain curves of 2219 aluminium alloy at different deformation temperatures and strain rate of 0.5 s-1

5 结 论

(1) 当应变速率相同时，变形温度越高，2219铝合金的流变应力、屈服强度、抗压强度越低；当变形温度相同时，应变速率越大，2219铝合金的流变应力、屈服强度、抗压强度越高。

(2) 由Fields-Backofen本构方程计算得到的2219铝合金应力的变化规律与试验得到的相同，且应力计算值与试验值的相对误差小于5%，该本构方程具有较高的精度。