以竞赛题为背景的数学命题策略研究

陕西 李 歆

数学竞赛题是数学命题专家经过深思熟虑后精心编制的经典题，对于选拔和培养数学人才具有重要的促进作用,竞赛题中所渗透的数学思想和方法对数学教学具有一定的引领性和指导性.但是,竞赛题往往思维难度较大,方法技巧较高,常常使多数学生望而生畏.因此，以一些熟悉的经典竞赛题为背景命制数学基础题，既是充实和丰富教学内容的需要,也是提升多数学生解题效果的有力保证.

一、利用竞赛题中的已知条件,合理引入变换,通过改变结构,获得新命题

【证明】如果联想到不等式(x+y)2≥4xy(*),则①式的证明就变得十分简单:

由此得到下列新命题:

【解析】仿照例1,利用(*)式可得

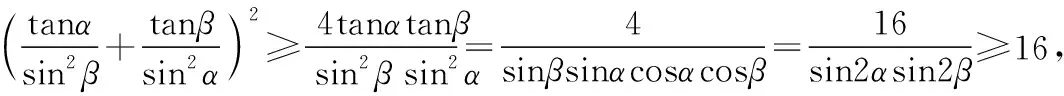
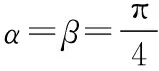
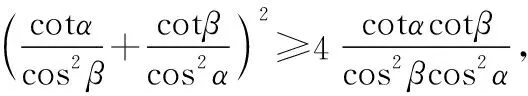
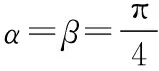
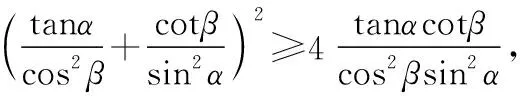
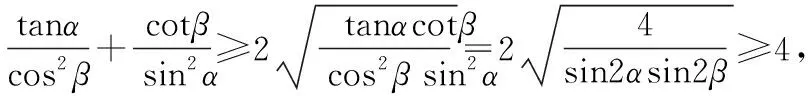
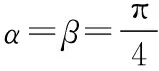
【评析】以上三道命题都是以例1为背景命制的基础性的题,它们在解法上都有一个共同点就是利用不等式(*)实现解题最关键的转化.同时,相对例1来说,命题1、命题2和命题3所考查的内容更加全面(如均值不等式、同角三角函数的基本关系式以及正弦函数和余弦函数的有界性等),基础性更强.

二、利用竞赛题中的多元特征,有效实施减元,通过优化组合,获得新命题

【例2】(第31届IMO预选题)已知a,b,c∈R+,求证:

(a2+ab+b2)(b2+bc+c2)(c2+ca+a2)≥(ab+bc+ca)3. ②

【分析】不等式②是一个三元不等式,结构对称但比较复杂,证明难度大,技巧性强,考虑二元情况,取c=1,则②式变为

(a2+ab+b2)(b2+b+1)(1+a+a2)≥(ab+b+a)3,

上式虽然变为二元不等式,但在形式上与②式没有多大变化,必须进行优化.

于是由上式得

两边同时乘以(a2+b2)2(a2+1)2(b2+1)2,得

≥(a2+b2)2(a2+1)2(b2+1)2(a+b+ab)3

≥43(ab)4(a+b+ab)3,

由此得到以下命题:

【命题4】已知a,b是满足ab≥1的正数,求证:

【证法1】(a2+b2)(a2+1)(b2+1)

≥2ab(a2b2+a2+b2+1)

≥2(a2b2+a2+b2+1)

【证法2】(a2+b2)(a2+1)(b2+1)

≥2ab(a2b2+a2+b2+1)

≥3(ab+a+b)+(ab+a+b)-4

在以上两种证法中,一开始都用到了如下一个不等式

(a2+b2)(a2+1)(b2+1)≥2ab(a2b2+a2+b2+1),

这说明将左边的三个因式项可以看成两个整体部分,即(a2+b2)与(a2+1)(b2+1),由此受到启发,经过探究发现,由2(a2+b2+1)=(a2+1)+(b2+1)+(a2+b2)≥2a+2b+2ab得a2+b2≥a+b+ab-1. ③

由2(a2+1)(b2+1)=(a2+1)+(b2+1)+(a2+b2)+2a2b2≥2a+2b+2ab+2得(a2+1)(b2+1)≥a+b+ab+1. ④

将不等式③与④两边分别相乘,就得到命题4的一个加强命题:

【命题5】已知a,b是满足ab≥1的正数,求证:

(a2+b2)(a2+1)(b2+1)≥(a+b+ab)2-1.

【证明】事实上,只要证明:

⟺3(a+b+ab)2-8(a+b+ab)-3≥0

⟺[(a+b+ab)-3][3(a+b+ab)+1]≥0,

【评析】从结构上看,命题4和命题5无论是题设条件,还是所要求证的不等式都与例2大相径庭,完全脱胎换骨为两道数学新题;从解题方法上看,例2因为难度大,多数学生往往感到入手难,思路无法打开,但命题4和命题5因为降低了难度,而且结构相对简单,因此容易激发多数学生探究性学习的兴趣,解题效果会更佳.

三、利用竞赛题中的复杂结构,采取减换并举,通过降低难度,获得新命题

【例3】(第20届伊朗数学竞赛题)已知a,b,c为正实数,a2+b2+c2+abc=4 ⑤,求证：a+b+c≤3.

【分析】该题作为一道条件不等式题，却与常规问题有所不同，题目所给的条件等式的结构比待证的不等式还要复杂，因此,由条件等式入手,先作减元处理,可以让复杂的问题变得简单一些.如:

取c=b,则⑤式变为a2+2b2+ab2=4，

整理得a+b2=2, ⑥

取c=1,则⑤式变为a2+b2+ab=3, ⑦

当且仅当a=b=1，即x=y=1时等号成立.

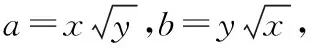
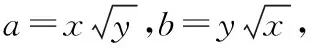
解得a+b≤2，当且仅当a=b=1时等号成立.

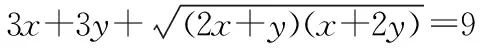
当且仅当x=y=1时等号成立.

【评析】从命题6到命题9，条件式与问题式看上去比较复杂,但只要从中找出共同点,并恰当地借助例3的解法——换元法,即可顺利获解,这对于培养学生的观察能力、转化与化归能力等基本的数学素养大有裨益.

四、利用竞赛题中的潜在联系,运用数学方法,通过等价转化,获得新命题

【分析】不等式⑧又被称作“Nesbitt不等式”,将它作化整处理得2(a3+b3+c3)≥a2b+ab2+b2c+bc2+c2a+ca2. ⑨

由于a2b+ab2+b2c+bc2+c2a+ca2=(a+b)(b+c)(c+a)-2abc,

所以,由⑨式得到以下命题:

【命题10】设a,b,c>0,求证:

2(a3+b3+c3+abc)≥(a+b)(b+c)(c+a). ⑩

【分析】如果对⑨式再加以整理,得

【命题11】设a,b,c>0,求证:

【评析】从命题10和命题11的命制过程来看,不等式与不等式⑧等价,不等式是不等式⑧的等价不等式⑨的放缩式改造,由不等式⑩和不等式,分别利用二元均值不等式和不等式⑧,都可得到三元均值不等式:a3+b3+c3≥3abc.因此,命题10和命题11既揭示了隐藏在不等式⑧背后的潜在联系,又对深化三元均值不等式的教学有着十分重要的指导作用.