基于负选择算法的自动路径测试*

张 华 陆 玉

(阜阳职业技术学院 安徽阜阳 236031)

软件测试是软件开发中不可避免的一个环节，是一个发现错误的过程[1]。软件测试可以自动或手动进行，是一个冗长而繁琐的过程，其所耗时间和资源一般占软件开发总成本的50%以上。软件测试最关键的一步是生成案例程序的测试数据。手工测试是一个冗长乏味的耗时过程，为满足测试的充分性标准，可以使用自动化的方式改进。这个过程被称为自动测试数据生成程序(automatic test data generation，ATDG)。

在结构测试中，测试数据的生成意味着搜索测试数据以执行所测试程序的内部结构，以满足选定的测试标准。有3种主要类型的结构覆盖准则：语句覆盖(即每个语句在程序中被执行至少一次)，分支覆盖(即每一个逻辑分支在程序中执行至少一次)，和路径覆盖(即每个不同路径在程序中都至少可以被执行一次)，文章将重点讨论路径覆盖。

路径测试是一种结构测试方法，主要的困难之一是如何生成一个有效的测试数据，在短时间内遍历程序的所有路径。为尽可能达到这一目的，路径测试方法涉及选择执行和查找测试数据以覆盖它的路径子集。研究人员亦已经提出了几种路径测试自动生成测试数据，比如使用随机、动态等方法，但这些方法不足以产生足够且合适的测试数据。

基于此，文章介绍了使用负选择算法(negative selection algorithm，NSA)进行路径测试自动生成数据的一种方法，这在人工免疫系统中最重要的算法，可以在确保目标路径的完整覆盖的前提下减少人工工作。

1研究动机和准备工作

路径覆盖的主要任务是产生有效的测试数据，通过程序遍历所有的逻辑路径。为模拟软件程序的执行路径，在测试之前需建立相关的控制流图(control flow graph，CFG)[2]。在程序中n种决策会有2n种可能的路径，即圈复杂度(cyclomatic complexity，CC)[3]，而程序中循环的存在会增加路径的数目，即每个不同数量的循环的迭代是一个不同的路径。手动测试因成本太高基本不可能实现，而即使是自动化测试生成工具也可能很难生成测试数据以获得完整的路径覆盖率，尤其是当程序包含嵌套循环时，故对于任何合理大小的程序，穷举方式不可行。 同样随机方法可靠性也不高，动态测试数据生成技术效率低耗时长，往往容易陷入输入数据域空间的局部最优状态。

为解决这些问题，很多科研者开始考虑使用基于启发式框架的算法作为生成测试数据的更好的替代方案，如遗传算法(GA)[4]、粒子群算法(PSO)[5]等。在上述方案中，遗传算法是在该领域最常用的启发式技术，可以提供稳定的结果并且有利于全局择优。大量研究结果表明，遗传算法比随机检验更有效、更有效，且其试验数据的质量也高于随机试验。PSO算法被广泛应用于各种优化问题中，具有收敛快、精度高等优点。然而，它受到了早产的影响，从而降低了测试用例生成的效率。

在以上方案的基础上仍需进一步提高过程的效率和有效性，故在此评估NSA对随机测试的有效性。文章希望NSA能自动生成一个更有效的测试数据来在更短的时间内遍历所有的程序路径。

2算法原理

路径测试是结构化测试的主要策略，解决路径测试的基本方法是在测试程序中找到可能覆盖路径的指定输入数据。为确保路径覆盖的完善度，文章希望使用一种自动生成测试数据的算法，该算法是通过定义一组根据数据集生成的自采样，然后生成检测器作为 NSA的主要组件之一来实现的。在此过程中首先随机生成检测器的候选种群，然后在迭代过程中将其训练成熟。

实验中需使用到汉明距离(hamming distance)[6]来定义检测器之间的距离。该算法以最大距离选择检测器，覆盖所有迭代域，直到满足停止准则算法结束。这里的停止条件是测试数据的最大数量。该算法的步骤如下：

输入：正在测试的程序

输出：测试数据集

步骤1：输入测试源代码下的程序；

步骤2：从程序源代码中构建CFG；

步骤3：计算CC的取值，见式(1)：

CC=P+1

(1)

其中P是谓词节点的数量，其中节点在CFG中有多个相邻节点。此值决定必须覆盖的独立路径的数量。

步骤4：随机生成初始的待选检测器(这些检测器代表测试路径数据集，即为CC的取值)；

步骤5：重复；

步骤6：生成新的测试用例；

步骤7：计算检测器之间的汉明距离D，见式(2)：

(2)

A和B是任意两个检测器。

步骤8：选择具有最大适应值的新一代检测器；

步骤9：继续执行，直到满足了停止条件或超过了最大代数。

3实验结果分析

文章选择了基准测试程序中的三角形分类器作为案例，使用 NSA算法与随机算法分别进行路径测试，并比较结果。

这个程序的机制是通过输入一组三边数据，使用分类器来确定它是不是一个三角形，或者进一步确认其三角形的类型。这个程序之所以被普遍使用，是因为即使使用了大量的整数，也只有少数组合满足代码中的特定分支。例如，使用范围从1-10的三边数值中只有12个组合可能是不等边三角形。另外，随机搜索最困难的路径是等边三角形路径，因为它必须找到三个相等的整数值。这使得三角程序成为软件测试和测试数据生成研究的极好的试验平台。

图1给出了程序的源代码和CFG的相应构造。CC值为4，这是谓词节点加上1的数量(谓词节点是CFG中有多个相邻节点的节点)。CC的值标识出程序独立路径的个数。

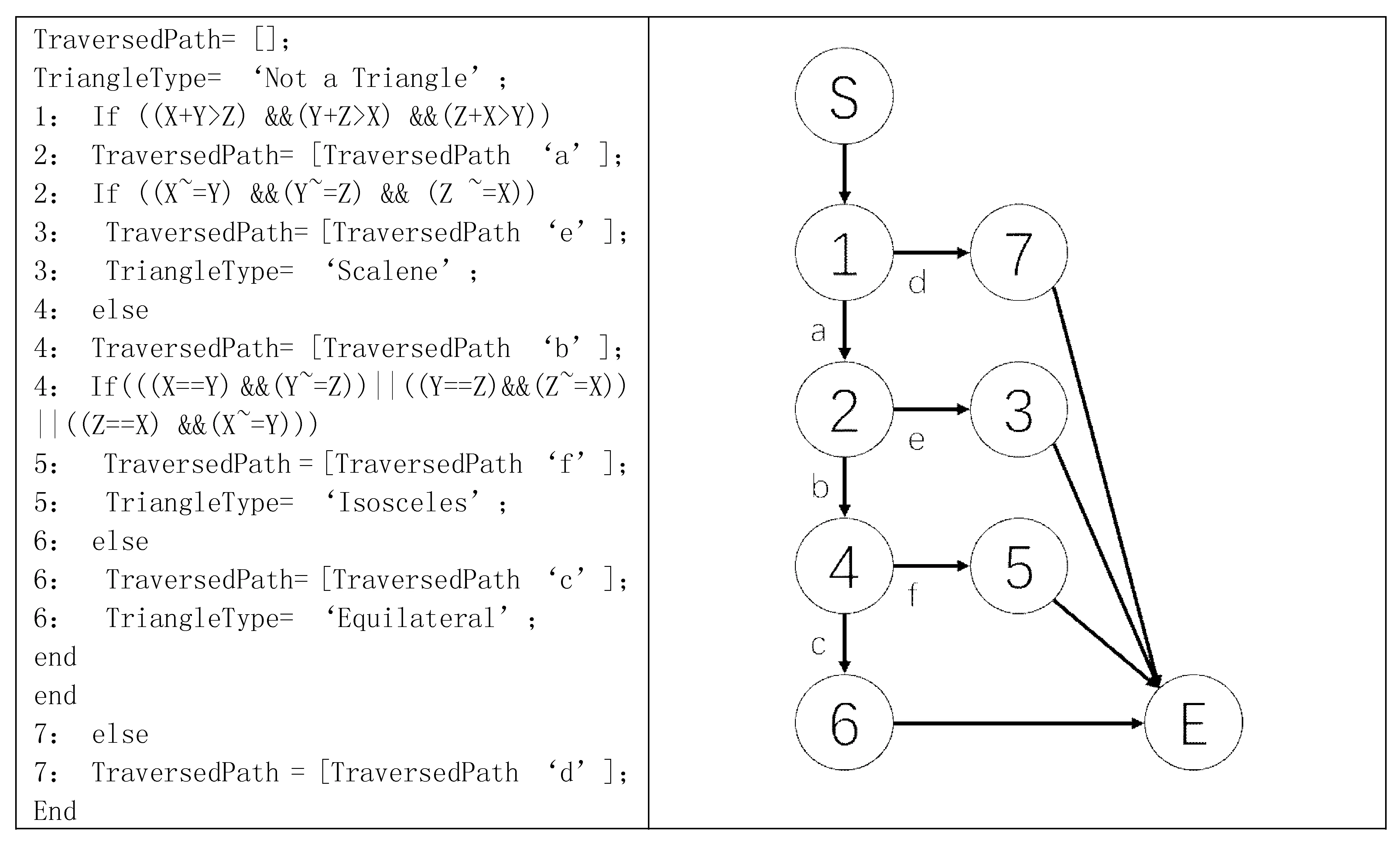
图1 三角分类器执行源代码及其相关控制流图

为简单起见将输入域作为1-10考虑3个整参数来对三角形进行分类(x，y，z)，用于覆盖程序路径的测试数据见表1。

实验中使用了1 000个测试数据来对比随机算法和NSA。结果表明，由于NAS可以将测试数据提前生成所需的路径，故其生成的测试数据质量优于随机算法。实验中选择十代数据，表2显示了当按图1所示进行两种算法测试时的各代测试数据路径数以及测试执行时间情况。

表1 生成的测试数据样本

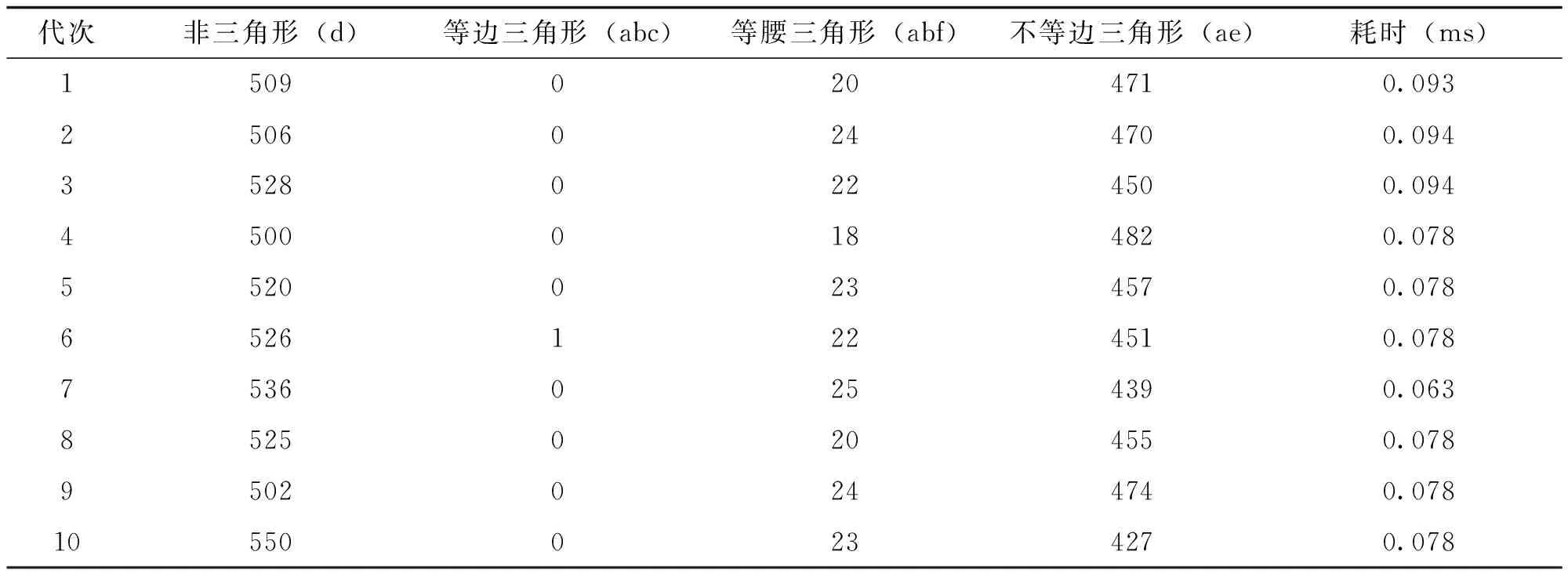
表2 随机算法测试时各代测试数据路径数及执行时间

表3显示了图1中的测试数据路径数以及使用NSA算法的测试时间执行情况。

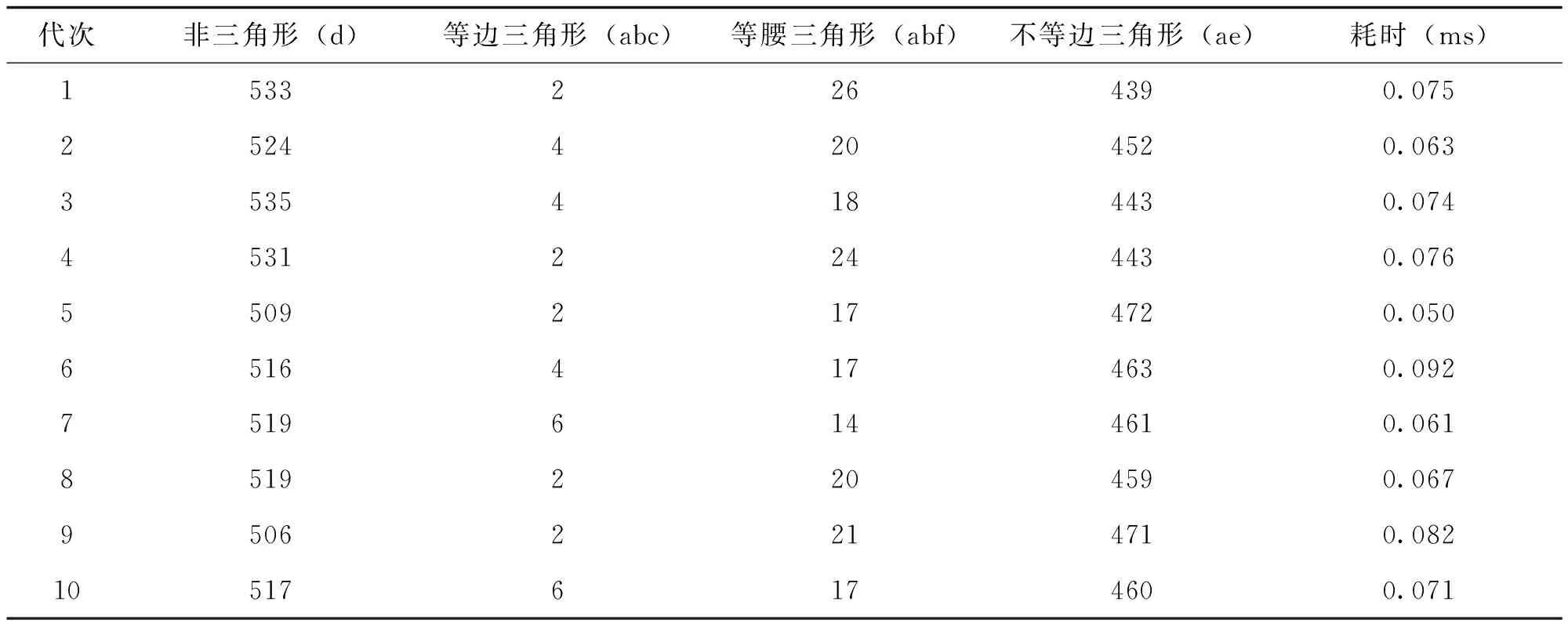
表3 NSA方式一代至十代测试数据路径数及执行时间

从表1和表2可发现，从分类三角形问题的1 000个测试数据中，已经生成了2个测试数据用于用该算法从第一代遍历等边路径。值得注意的是，随机测试时没有机会生成相同路径的测试数据，只在第六代中有一次机会遍历测试数据，如图4所示。

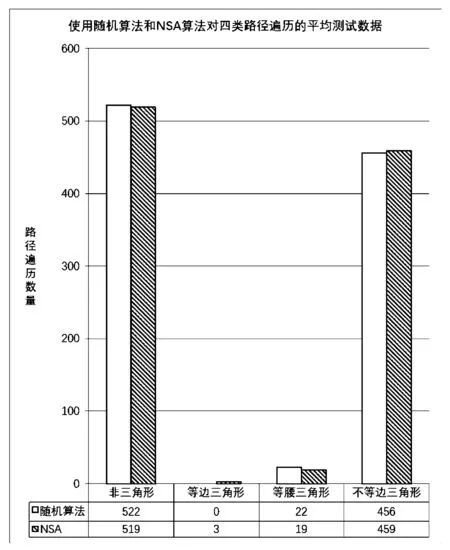
图4 使用NSA和随机算法覆盖路径的平均值比对

由图4可以看出，NSA在生成测试数据中比随机算法更能成功地覆盖所有路径，尤其是最困难的等边路径，比如NSA过程中遍历了3次而随机算法只有0.1次。与此同时，NSA比随机算法减少了67%的耗时，如表3所示。

为完善实验评估结果，文章加入了遗传算法的测试数据进行比对。图5显示了当同时遍历等边数据路径时，随机算法、NSA和遗传算法的执行数据结果。可见，使用NSA算法时等边数据的路径覆盖程度更加完善。

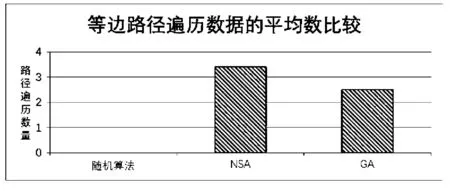
图5 3种算法在等边数值路径遍历中的比对

5结论

文章以三角形分类基准程序为例，使用负选择算法(NSA)进行了数据自动生成的路径覆盖率测试，结果表明该算法能够以较少的时间将搜索移动到所需的搜索范围，比随机生成算法更有效、更经济。为了完善评价结果，将此算法与遗传算法进行了比较，结果表明该方法确实能够提高测试数据的质量。在以后的研究中，该算法将在实验中使用更多的基准程序和不同的数据类型，以进一步评估算法的性能。