龙门吊运输动力学分析和优化设计
2018-07-26徐沈阳熊友兵刘秀明
徐沈阳 熊友兵 刘秀明
(天津工业大学,天津 300387)
门式起重机是桥式起重机的一种变形,又叫龙门吊。龙门吊作为一种运输机械被广泛应用于工程方面[1],国内外的专家和学者对此系统的研究也早已开始,但是缺少对运动的动态分析和评价。如何通过使用模型进行合理的设计后能够满足安全、高效的需求以完成检测已成为各位专家和学者密切关注的问题[2-3]。吊车运动过程中会引起货物的摆动,合理进行防摆控制是提高吊车工作效率和安全性的重要手段[4]。本文通过深入分析货物摆动的动态过程,研究货物摆动对系统的影响,这对货物的消摆具有重大意义。
1.动力学分析
1.1 运动状态分析
由于货物摆动过程中,缆绳受力随速度、摆角等因素的变化而变化,导致缆绳长度会产生一定的伸张,从而对摆角等因素产生影响。本文只分析货物摆动过程中缆绳长度不变的情况。
另外,由于货物运动时,其所受空气阻力难以简单界定,受到多种因素的影响。因此,在理想状态下(忽略空气阻力)研究问题,能更加方便、准确地得出结论。本文忽略货物摆动过程中空气阻力对负载的影响。根据达朗伯原理[5],对货物m进行受力分析,得到系统的微分方程:
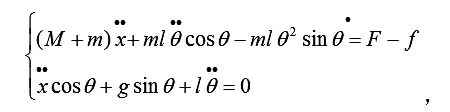
运用 MATLAB求解方程组[6-7],绘制吊车运动速度曲线、摆角随时间变化曲线以及货物在平衡位置振动时摆角变化曲线,可得吊车加速至匀速阶段的运动过程。本文给出了摆角和平衡位置的定义。
(1)摆角:缆绳与竖直方向的夹角;
(2)平衡位置:货物在某摆角处不停振荡的中心位置。
通过对两个微分方程的求解,可以得到在系统加速阶段各物理量的变化情况,如图1、图2所示。
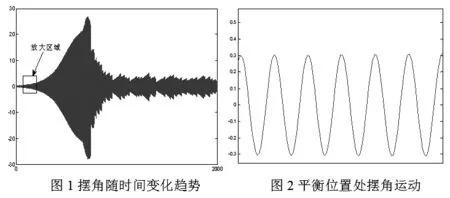
由图1可知,货物摆角由初始状态零度开始增大,随着吊车速度增加,货物摆角恒为正值且逐渐减大,在加速阶段结束时摆角的大小为在匀速运动阶段摆角的峰值。匀速运动阶段,货物摆动的平衡位置为零位置;吊车在减速运动阶段,货物的摆角为负值且逐渐减小;最终吊车匀速阶段,货物在零位置附近摆动。
由图2可知,货物在每个平衡位置不停振动,类似简谐运动。
1.2 运动过程
根据吊车运动曲线,可将整体运动过程分为四个阶段。第一阶段为吊车匀加速阶段,摆角由最大位置逐渐减小并在每个平衡位置不停振荡做简谐运动;第二阶段为吊车匀速阶段,货物的平衡位置为零位置,在零位置附近不停振荡;第三阶段为吊车匀减速阶段,货物摆角变为负值;第四阶段为吊车匀速阶段,货物从负最大摆角回到零位置。
1.2.1 加速阶段
货物摆动的模型如图3所示。吊车加速时间为t1,匀速运行时间为 t2,减速时间为t3。m1为吊车质量,m2为货物质量,θ为货物的摆角,F为小车所受合外力,FT为缆绳的拉力,l为缆绳的长度。货物在摆动过程中θ比较小,可近似认为Sinθ≈θ,cosθ≈1。
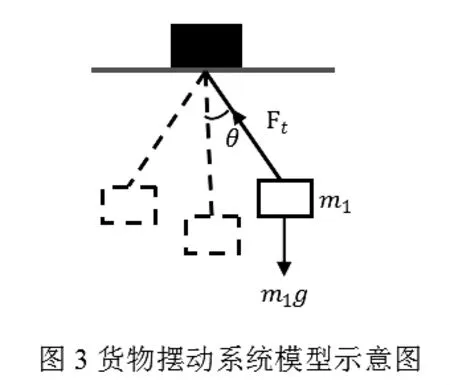
设小车与货物的坐标分别为(x,0)、(xm,ym),则有

忽略缆绳的形变,则上述方程可简化为

根据坐标关系,可以得到系统的动能为

拉格朗日方程标准形式[8]为

该系统的拉格朗日方程为

将式(1)分别带入式(2)、(3)中可得

采用Laplace变换的方法对两个微分方程进行求解[9-10],吊车开始加速,货物由零位置开始摆动,故初始条件为

经过Laplace变换得

求Laplace逆变换得

对于缆绳受力,对吊车应用牛顿第二定律得

将(4)式带入上式得货物在摆动过程中对系统水平方向的力为
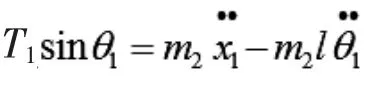
其中,T1为缆绳的拉力,θ1为第一阶段运动的摆角。
1.2.2 匀速运动阶段
吊车经过时间进入匀速阶段,货物过渡到在零位置摆动的阶段,式(5)变为
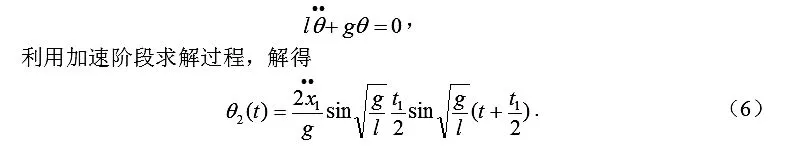
利用加速阶段求解过程,解得
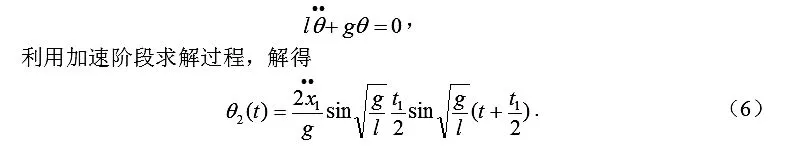
1.2.3 减速运动阶段
类比吊车在加速阶段的动力学分析,第二阶段匀速运动摆角的末值为减速阶段的初始值,对式(6)求Laplace反变换可得

1.2.4 最终匀速运动阶段
第四阶段匀速过程可类比第二阶段匀速过程,摆角变化为负值,得到微分方程

利用加速阶段求解过程,解得

2.运输模型的建立
2.1 目标分析
运输过程中,运输效率是评价运输方案优劣的指标,本文定义系统运输效率为单位时间内运输货物的重量
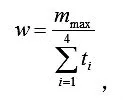
2.2 约束分析
(1)距离约束
前三个阶段运动距离D1为

吊车第一阶段做加速运动,初始状态为静止的,即:v1=0。
吊车第二阶段做匀速运动,初始速度为吊车所达到的最大速度,等于第一阶段运动末速度,即:v2=a1t1。
吊车第三阶段做减速运动,初始速度等于匀速阶段速度,即:v3=v2=a1t1。
第四阶段运动距离 D2为:D2=v4t4。
吊车第四阶段做匀速运动,初始速度为减速时间后的速度,即:
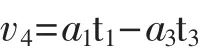
(2)时间约束
由整个调运时间不超过最大可接受时间,可得

其中,Tmax为四个阶段的总时间,ti为第 i个运动阶段时间。
第一阶段和第四阶段吊车运动加速度大小相等方向相反,由于在第四阶段吊车仍有速度,则可知加速阶段时间大于减速阶段时间,即

(3)速度约束
货物第三阶段运动最终摆动速度和最终时刻的摆角,决定了第四阶段货物的水平速度。
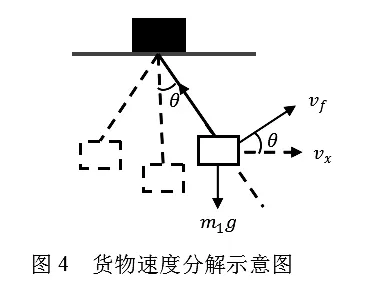
如图4,对货物的摆动速度分解得到

式中vf3是第三阶段末货物的摆动速度,vx是货物运动的水平速度。
(4)摆角约束
第四阶段匀速过程可类比第二阶段匀速过程,摆角变化为负值,得到微分方程

利用Laplace变换求解微分方程,解得

其中θ4为第四阶段匀速运行时货物的摆角。
受力分析得出的每个阶段摆角的函数,设过程中允许的最大摆角为θmQX,得到如下限制

式中θ4为第四阶段匀速运行时货物运动的摆角。在寻求最终目标时,采用保守策略是稳妥的,即在最坏的情况下寻求最好的结果,所以采用极小极大法求解。由于货物在平衡位置不停地振动,求出货物最大的振动摆角,使该角度最小,即为所要达到的摆动范围。
(5)缆绳承载力约束,缆绳受力不能超过其最大承载力范围限制为

3.实例分析
为了进行应用验证,本文选取了代表性较强的龙门吊配置进行分析:绳长15m,货物运动总长在75-80m之间,最大加速度为 1m/s2,最大运输时间为120s,缆绳最大承载能力为20000kg。利用MATLAB求解非线性规划问题,设置时间的精度为0.01,得到各个运动的摆角变化曲线如图4、图 5所示。

图4 第一阶段摆角变化图

图5第二阶段摆角变化图
图4 为第一阶段货物摆角变化,5.1s内货物的摆角逐渐向正方向增大,在1.2s时形成最大摆角,为 1.0813°。
图5为第二阶段货物摆角变化,第二阶段运动时间为16.8s,在该段时间内货物在零位置附近不停振动,在1.2s时形成最大的摆角,为2.5143°。

图6 第三阶段摆角变化图

图7第二阶段摆角变化图
图6 为第三阶段货物摆角变化,第三阶段运动时间为0.2s,摆角向负方向逐渐增大,在21.3s时形成最大摆角,为-2.2877°.
图7为第四阶段货物摆角变化,第四阶段运动时间为28s,摆角在零位置附近振动且摆角很小。在35.2s时形成最大摆角,为-2.1686°。
综上所示,运输过程中,总时间为53s,运动时间和摆角关系如表1所示。

表1 运动时间和最小摆幅
此时的加速阶段的加速度为0.83m/s2,调运质量为6050kg。求解出的四个阶段摆动均比较小,保证货物安全。加减速时间较短,两段匀速时间较长,货物平稳运动时间较长,符合实际吊运情况。
更改上述实例中目标为调运质量最大,利用建立模型进行模拟,得到模拟结果如表2。
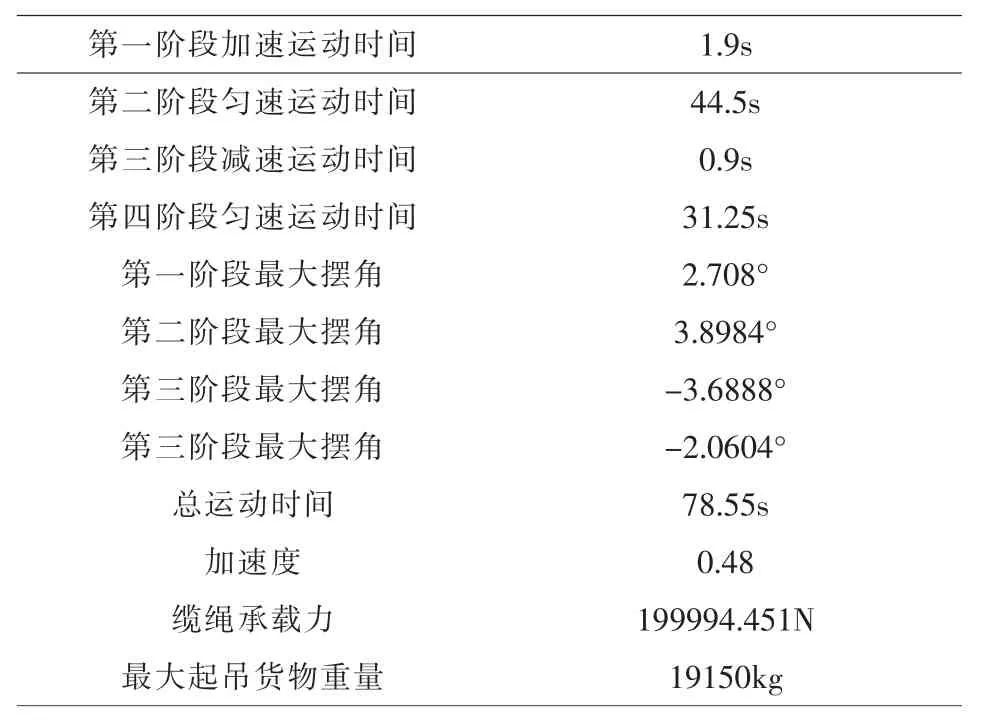
表2 调运质量为目标求解
两实例进行对比,可以得到,实例1中保持运输效率最高,但单次运输质量较小,更改目标后的实例2以质量最大为目标,虽增加了单次运输质量,但过程中摆角也有所增加。
该模型能根据实际需求,调整参数,更改目标和约束,得到运输过程以摆角最小、运输效率最高、运输质量最大等为目标的方案,更符合运输过程中的实际情况,对实际运输具有重要指导意义。
4.结语
龙门吊系统在运输过程中的工作状况是多变的,可根据不同需求,修改本文实例中的缆绳最大承载能力、绳长、运输长度、最大加速度等参数,得到最适合的运输方案。本文从力学的角度,结合现有的理论基础,分析不同状态下的受力情况,利用非线性规划建立了摆角非线性规划模型,以此来分析运动过程,具有良好的效果。
对于龙门吊运输问题,利用仿真模拟的方法得到运输过程中最佳配置,对实际运输具有十分重要的参考价值。但由于不同变量之间关系复杂,需要不断加深对运输过程的研究,以实现运输的高效、智能的控制。
