基于码重分布信息熵的线性分组码盲识别方法*

陈金杰，杨俊安

（1.91245部队，辽宁 葫芦岛 125000；2.国防科学技术大学，安徽 合肥 230037）

0 引 言

为了提高通信信息传输的可靠性和稳定性，目前越来越多的数字通信系统采用了各种信道编码技术。通信技术与信道编码理论的不断发展与完善，给信息对抗领域的信道编码识别提出了挑战。线性分组码作为信道编码中的一种重要编码方式，编、译码结构简单，检错或纠错性能优越，已被广泛应用于军事和民用通信[1-3]。

实际通信环境中，由于噪声、干扰、时延及信道衰落等因素的影响，对接收或截获的信号经过解调等处理所获得的编码序列存在误码的情况不可避免。鉴于此，具有较高容错性能的线性分组码盲识别方法，在信息对抗或智能通信等领域中具有重要的应用价值[4-9]。然而，现有的一些线性分组码盲识别方法在应用于数据识别分析时存在运算较复杂、容错性一般等问题，严重影响着识别方法的实际工程应用前景。

本文针对线性分组码编码特点和性质，在分析现有识别方法的基础上，引入了信息熵的概念，提出了一种基于码重分布信息熵的线性分组码盲识别方法。在先验知识不同的条件下，利用该识别方法能够正确识别出线性分组码的码长或码字起始点，从而进一步识别线性分组码的其他编码参数。最后，通过仿真实验验证了识别方法的有效性，同时具有较好的容错性能。

1 基于码重分布信息熵的盲识别方法

1.1 码重的概念和性质

[n,k]线性分组码中，一个完整码字中码元“1”的个数定义为码重，也称Hamming重量。它是线性分组码的一个重要参数。[n,k]线性分组码的Hamming重量的分布情况定义为码重分布。它不仅是探索码结构的重要窗口，而且是计算各种译码错误概率的主要依据之一。通过它能较好地掌握码的内部关系。这里，将码字C的码重分布表示为W(C)，即表示码字C中Hamming重量等于d的码字的数目。

定理1：在一个数字通信系统传输过程中，一个码组中同时发生t+1个错误的概率要远远小于同时发生t个的错误概率，即：

实际数据传输中，信道误码率在10-4～10-3之间，就可以称为高误码率。由此可见，P(2)＜＜P(1)。此时，误码对码重的改变仅为±1。同时，结合定理1，当码字中存在误码时，对码重的改变并不显著。因而可以说，误码对码组的码重分布影响很小。所以，可利用线性分组码的码重分布来识别线性分组码的某些参数。

定理2：由线性分组码[n,k]的k位信息码元所生成的n位码字集合v(2k)，一定是n维向量空间V(2k)的k维子空间，且在向量空间V中分布的概率不同。

由定理2可知，[n,k]线性分组码生成的码字集合为2k（2k＜＜2n）。由k位信息码元编码生成的n位线性分组码字集合v包含于n位码元组成的码字集合，且前者在n位码元组成的码字集合中的分布概率不相等，推理出[n,k]线性分组码不等码重的码组出现的概率也是不等的。

1.2 熵的概念和性质

信息熵是系统状态不确定性的定量评价指标，对于系统内在信息具有较强的刻画能力。以下在对信息熵概念和性质进行阐述的基础上，研究用于线性分组码编码参数的识别上，提出基于码重分布信息熵识别线性分组码的盲识别方法，通过理论分析和仿真实验验证其有效性。

设具有n个状态的信源为X={xi,i=1,2,…,n}，每个状态出现的概率为P={pi,i=1,2,…,n}，则该信源的信息熵可表述为：

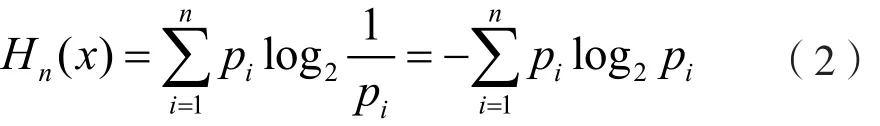
信息熵是表征信源总体特征的一个量，同时是信源输出信息的不确定性和各信源出现随机性的量度。

关于信息熵H(x)具有以下一些基本性质[10-11]。

（1）非负性。因为0≤pi≤1,i=1,2,…,n，所以log2pi≤0，即推出-pilog2pi≥0，从而由式（2）可知，该式是不小于零的。

（2）极值性，即：

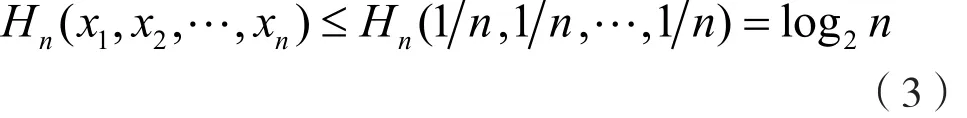
（3）熵的灵敏度。熵函数的灵敏度是熵函数对于概率分布函数中的细微变化的反应情况的衡量。文献[12]给出了详细证明，结果就是当概率分布发生微小变化时，熵值变化也会很小。

由信息熵的概念及其性质可知，若对单个信道进行分析时，信号越简单，能量就越集中于少数几个模式，最终计算得到的熵值越小；相反，信号越复杂，能量就越分散，其结果熵值就越大。

1.3 识别方法的提出

根据线性分组码编码特点和信息熵的性质，将信息熵的概念应用到对线性分组码的码长识别中。定义码重信息熵为：

式中N表示样本中的码字总数；nχd表示码重为d的码字在码字总数N中出现的个数。

当以码字起始点作为先验知识的条件下，对线性分组码的码长进行识别时，若估计值不等于真实码长或整数倍的真实码长时，其序列无完整的线性约束关系。然而，不同码重的码组是等概率出现的，即在码长的估计值范围内码重分布越分散，其结果熵值就越大。最终，随着估计值的增大，不同码重的码组出现的概率趋于1/(n+1)，其所计算的熵值也趋于一个稳定值。当估计值等于真实码长或整数倍的真实码长时，其序列具有完整的线性约束关系。由线性分组码的码重分布特点可知，其分布是非等概的，即计算的熵值对比一个码长范围内的邻近的值是最小的。因此，由计算结果易于识别出码长或码长的倍数。在获得码长后，需进一步计算该编码的生成矩阵G及其他编码参数。

当以线性分组码的码长作为先验知识的条件下，可实现对码字起始点的识别。若截取一个固定码长的码字的起始位不是码字的真实起始点，则该码字不是完整的线性分组码码字，且无线性约束关系，其不同码重的码组趋于等概率出现。若截取一个固定码长的码字的起始位恰好是线性分组码的码字起始点，则该码字将是一个完整的线性分组码的码字，相应的内部具有完整的线性约束关系。依据线性分组码的码重分布特点，不同码重的码组出现的概率是非等概的，即利用码重分布信息熵函数可以识别码字中某一点为该码字的起始点，进而依次完成其他编码参数的正确识别。

1.4 条件一：码字起始点i为先验知识的识别方法分析

首先，在码字起始点i已知的条件下，利用码重分布的信息熵函数识别出码长。其次，依据线性分组码的性质，完成其他编码参数的识别。最后，通过仿真实验，验证识别方法的有效性。

1.4.1 识别码长

信息传输过程中，对数据进行解码等处理后得到编码序列C。通过数据分析已知线性分组码的起始点c1下，截取序列样本长度nd，记为C={c1,c1,…,cnd}。

识别码长具体步骤如下：

步骤1：将长度为nd的编码序列C={c1,c1,…,cnd}由估计的码长n拆分为N个码字，即Ni={c1+(N-j)n+c2+(N-j)n+…+cn+(N-j)n}，j=N, N-1,…,1。若码长n不能被nd整除，则将nd-nN舍去。

步骤2：计算所有码字Ni的码重，分别表示为dj=c1+(N-j)n+c2+(n-j)n+…+cn+(n-j)n，将码重d出现的不同值记录为：Dd={dj}, j∈{1,2,…n}，同时将不同码重的分布表示为 W(C)={nχd},d ∈ {0,1,2,…n}，且sum(nχd)=N,d ∈ {0,1,2,…n}。

步骤3：利用式（4）计算线性分组码的码重分布信息熵Sn。

根据不同线性分组码的码重分布的非等概性质和完整码字之间的线性约束关系，由步骤3计算出信息熵Sn，一个码长范围内的最小值Sn对应值n即为码长或码长的倍数。

1.4.2 生成矩阵及其他编码参数求解

对于线性分组码[4]，任一[n,k]线性分组码均是由生成矩阵G线性表示的；反之，若将线性分组码的一组码字的码元排成m行n列(m＞n)的矩阵，然后对该矩阵初等行变换，则前k行化成[IkP]形式，余下m-k行为0，即：

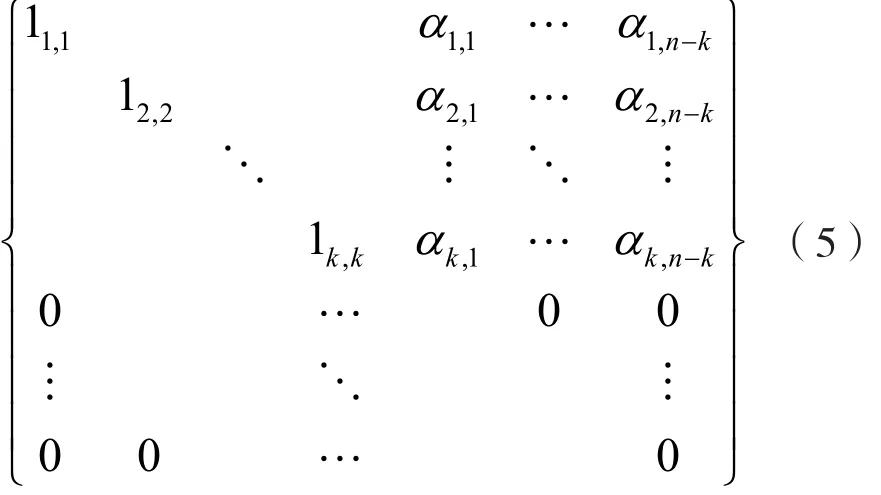
为实现生成矩阵的求解，可根据线性分组码的性质，在识别码长的分析过程中，记录步骤2的码重d出现的不同值Dd={dj}, j∈{1,2,…n}及不 同 码 重 的 分 布 W(C)={nχd},d ∈ {0,1,2,…n}， 且sum(nχd)=N,d ∈ {0,1,2,…n}。利用 W(C)集合内的较大值对应的码字，构建m行n列(m＞n)的分析矩阵，并进行初等行变换。当矩阵的每一行无错误码元时，化简后的矩阵前k行为[IkP]，且其他m-k行为0。最终，化简后的矩阵中前k行即为线性分组码的生成矩阵G。

在求解出生成矩阵G后，由C=MG可知解调等处理后的码字序列ci,i∈[1,n]为输入原信息序列mi,i∈[1,k]的线性变换，推出GHT=0，从而求得校验矩阵H=[PTIn-k]，而所要识别的信道编码参数均易获得。

最后，本文采用文献[13]中验证识别结果的基本思路，验证上述识别信道编码参数的正确性。首先选取一定长度的编码序列，设定大于实际通信环境下的信道误码率，由选取编码序列与信道误码率计算该选取长度序列中的错误码元，依据统计最大化原则，设定每个错误码元分布在不同码字，则可得含错误码元的码字占该编码序列中所有码字的比例ξ，并定义判决门限T=1-ξ。利用校验关系CHT=MGHT=0，当对所选取的码字计算校验关系成立的概率大于判决门限时，生成矩阵求解正确，完成识别；否则，利用上述求解生成矩阵的方法重新识别，直至结果正确。

1.4.3 识别流程

按照上述识别步骤的分析，在码字起始点i为先验知识条件下的识别方法流程如图1所示。

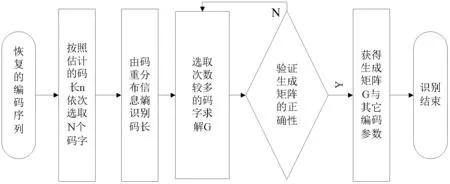
图1 码重分布信息熵识别方法流程

1.4.4 实验设计与仿真

为验证基于码重分布信息熵的线性分组码的盲识别方法的正确性，同样对文献[14]采用的4种典型线性分组码进行仿真实验。在无误码条件下，对所选取的4种线性分组码的仿真结果如图2所示。

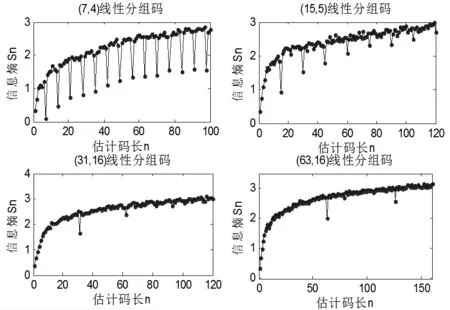
图2 4种线性分组码仿真

由图2仿真结果分析可知，若估计值不等于码长或码长的整数倍，计算的码重分布的信息熵的值对比与前一点的值或后一点的值均变化不大；而当估计值等于码长或码长的整数倍时，则计算的码重分布的信息熵的值对比与邻近点的值变化较大。由信息熵的特点可知，该点的值是一个码长范围内的最小值，从而验证了基于码重分布信息熵识别码长的有效性。

基于上述识别方法，进一步以[31,16]线性分组码为例，设定误码率P=1.5×10-2的条件下的仿真实验，结果如图3所示。

图3 误码条件下的[31,16]线性分组码的仿真

通过对比图2、图3发现，含有误码条件下的码重分布信息熵Sn的变化规律与无误码时的变化规律相同，只是在码长或码长的整数倍时码重分布信息熵Sn的值相对于邻近点的值变化较小，但是依然可以识别出正确结果，即码长为31。当码长n=31时，码重d出现的不同值D对应的不同码重的分布W如表1所示。

通过表1可知，当码重d为15、16时，对应的码字在码组中各占25.5%、30%。按照上述识别方法，选取码重值为15、16对应的码字构建分析矩阵，并进行初等行变换，得到生成矩阵G，如式（6）所示。由H=[PTIn-k]和式（6），可求得校验矩阵H。

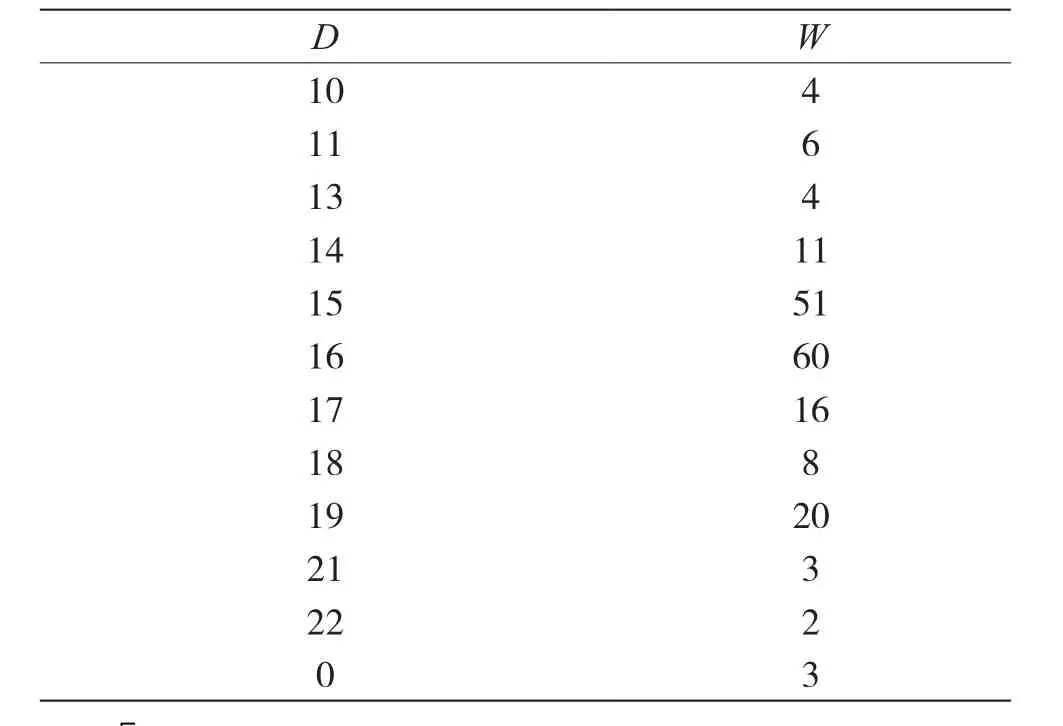
表1 n=31时线性分组码的码重分布

为验证生成矩阵G是否正确，预先设定判决的门限T。正常条件下，已知通信常规信道的误码率不高于10-3。根据实验需要，设定仿真数据的误码率为2×10-2，即大于常规信道的误码率，因此可由仿真数据样本长度计算错误码元的个数。依据统计最大化原则，设定错误码元分布在不同的码字中，计算出判决门限T=1-ξ=48%。对于上述[31,16]线性分组码样本中所有的码字，利用CHT=MGHT=0进行计算。它成立的概率为71.2%，大于判决门限，证明生成矩阵是正确的。由生成矩阵G得信息位k等于16，码率等于16/31。

1.5 条件二：码长n为先验知识的识别方法分析

在以码长n为先验知识的条件下，识别码字起点i、生成矩阵G及其他编码参数。识别过程基本与条件一的识别过程类似，在码长n已知的条件下该识别方法首先识别出码字起始点，其次求解生成矩阵G和其他编码参数，完成识别。

1.5.1 识别码字起始点

以线性分组码的码长n为先验知识，截取长度等于nd的编码序列，记为C={c1,c2,…,cnd}。

具体识别步骤如下：

步骤1：以q位开始，截取长度为nd的编码序列C={c1,c2,…,cnd}；以该线性分组码的码长n为基础，共计取N个码字为Nj={c1+(N-j)n+c2+(N-j)n+…+cn+(N-j)n}，j=N, N-1,…,1，并将nd-n·N码元舍去。

步骤2：由选取的N个线性分组码的码字构建分析矩阵，且矩阵的行数N大于列值n；构建的分析矩阵的每一行将是该起始点的完整码字。

步骤3：计算分析矩阵中每一行码字的码重， 即 dj={c1+(N-j)n+c2+(N-j)n+…+cn+(N-j)n}， 并 记 码重d出现的不同值Dd={dj}, j∈{1,2,…n}，同时W(C)={nχd},d∈{0,1,2,…n}表示不同码重的分布，且sum(nχd)=N,d ∈ {0,1,2,…n}。

步骤4：利用式（4）计算Sn。

步骤5：依次遍历起始位q，并返回步骤:1，同时定义q遍历的范围为0≤q≤2n+1。

由线性分组码码重分布的非等概性，可根据上述计算过程解得信息熵Sn。当Sn为最小值时，所对应的q点为线性分组码的码字起始点。

1.5.2 生成矩阵求解及其他编码参数的识别

在获得线性分组码的码长与码字起始点后，计算线性分组码的生成矩阵，与条件一的情况完全一致。选取码重分布W(C)集合内的较大值，由较大值对应的码字构建分析矩阵，并进行初等行变换。当矩阵中所选取码字不含错误码元时，化简后的分析矩阵前k行为[IkP]形式，其他m-k行为0，即前k行为生成矩阵G。验证生成矩阵的正确性和求解其他编码参数，参照条件一即可分析完成。

1.5.3 识别流程

按照上述识别步骤的分析，在码字起始点i为先验知识条件下的识别方法流程如图4所示。

图4 码重分布信息熵识别方法流程

1.5.4 实验设计及仿真

为验证基于码重分布信息熵识别码字起始点的正确性，同样采用1.4.4章节中4种线性分组码进行仿真实验，利用Matlab随机编码数据，随机从中截取数据样本长度为2×104bit，在未添加误码的条件下，利用码重分布信息熵识别码字起始点，如图5所示。

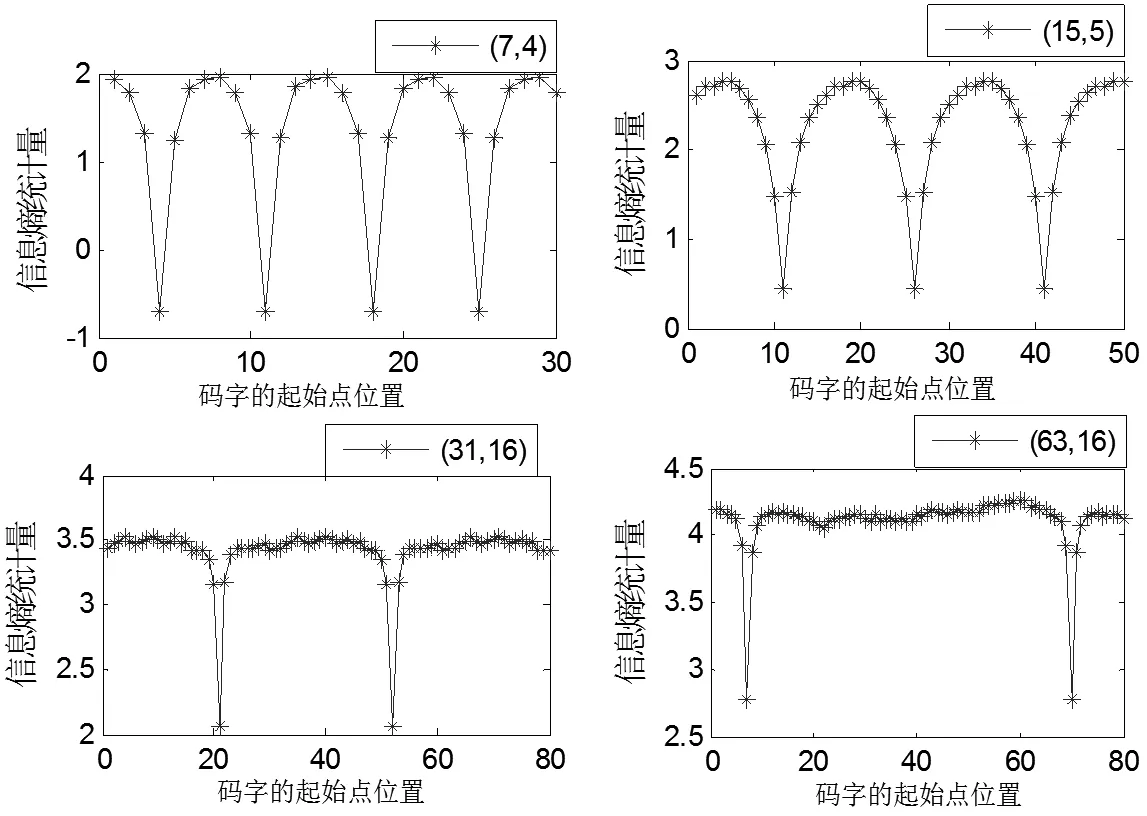
图5 码重分布信息熵识别码字起始点仿真

当q移位至码字起始点时，信息熵Sn相对邻近点的值变化较大；相反，当q移位至非码字起始点时，其截取的N个码字均不是一个完整的线性分组码的码字，计算的信息熵Sn变化就相对平缓。因此，根据码重分布的信息熵Sn值的变化，即可以识别出码字起始点i。从图5得知，4种线性分组码的码字起始点分别在仿真数据样本的第4位、第11位、第21位与第7位。

进一步以[31,16]线性分组码为例，同样，设定误码率P=1.5×10-2的条件下，选取N=200个码字进行仿真实验，结果如图6所示。

图6 码重分布信息熵识别码字起始点仿真

当n=31时，D对应的不同码重分布W如表2所示。

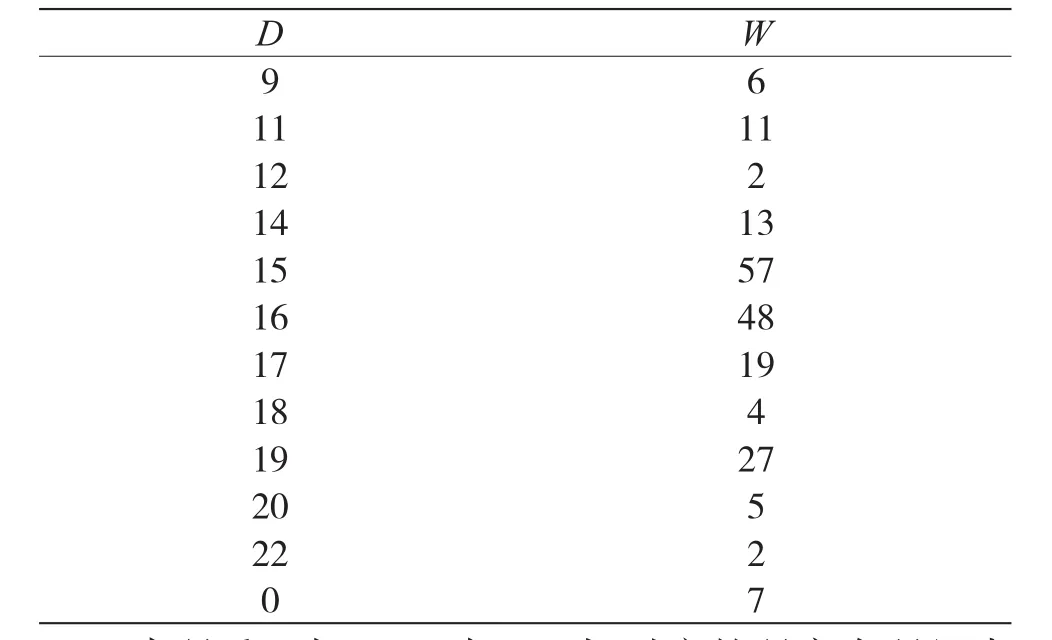
表2 n=31时的码重分布

当码重d为15、16与19时，对应的码字在码组中所占的比例较大，分别为28%、26%与13.5%。因此，将选取上述3种码重对应的码字构建m行n列的分析矩阵（m＞n），并对构建的分析矩阵进行化简，获得的生成矩阵G与式（6）相同。同理，由H=[PTIn-k]和式（6）可求得校验矩阵H：

为验证生成矩阵的正确性，同样设定判决门限T。判定方法与条件一时完全相同，这里不再赘述。

2 结果分析

不同先验知识条件下，利用码重分布信息熵正确识别码长或码字起始点，成为对应的整个识别过程分析的关键步骤，也是正确识别其他信道编码参数的基础。因此，码重信息熵识别码长或码字起始点的性能分析至关重要。

2.1 计算复杂度

通过码重分布信息熵式（4）识别码长，与文献[14]码重距离识别方法对比，若接收[n,k]线性分组码，则利用式（4）遍历估计值求解时均减少N次的加法与N次的平方运算。因此，随着识别线性分组码的码长增加，利用码重分布信息熵平均计算复杂度对比与利用码重距离识别码长的计算复杂度将有大幅减少。

2.2 容错性分析

选取上述4种线性分组码，分析码重分布信息熵识别方法的容错性，其各参数设置如表3所示。各生成1×104组仿真数据，利用码重分布信息熵分别识别码长与码字起始点，最终统计在不同误码条件下的识别概率，如图7所示。

表3 待测试的线性分组码

图7 码重信息熵识别的概率曲线

由图7可知，正确识别码长或码字起始点的概率均随线性分组码的码长增加而降低。由线性分组码的性质易知，当线性分组码的码长变长时，其线性分组码的码重取值增多、码重分布范围变大。所以，随着码长的增加，正确识别出码长与码字起始点的概率变低。同理，随着误码率的增加，正确识别的概率减小。但是，由图7中对[7，4]线性分组码识别码长的概率曲线可知，当误码率为5×10-2时，正确识别出码长的概率超过了90%；同样，对于[63，16]线性分组码，当误码率为1×10-2时，正确码长或码字起始点识别的概率也高于70%，且均满足生成矩阵与编码参数的正确求解。另外，对比文献[14]的识别方法，本文提出的识别方法的容错性优于码重距离盲识别方法的容错性；同时，由图7的右图也可以看到，该识别方法识别码字起始点的容错性要优于识别码长的容错性。

3 结 语

本文针对线性分组码码元之间的线性约束关系和码重分布的非等概性，结合信息熵的概念和性质，提出了一种线性分组码盲识别方法。在不同的先验知识条件下，通过计算码重分布的信息熵，正确识别出码长或码字起始点，进而求解出线性分组码的其他编码参数完成识别。由于信息熵函数不需要较复杂的运算，一定程度上减少了识别方法的计算复杂度，同时提高了识别方法的容错性。最后，对提出的识别方法进行了大量的仿真实验，一定条件下证明了识别方法的有效性。