基于LMS的检后盲自适应XPIC算法仿真*
2018-07-26王宇舟王春蓉
王宇舟,王春蓉,陈 颖
(1.中国西南电子技术研究所共性技术部,四川 成都 610036;2.空军驻电子十所军事代表室,四川 成都 610036)
0 引 言
为了提高系统频谱效率、增加系统容量,高速卫星通信系统一般采用同频复用的正交双极化传输技术。但是,对于两个频率相同的正交极化信号,由于传输信道的非理想特性(电离层去极化、天线物理误差、以及降雨、冰晶、尘暴等)易引起去极化现象,导致交叉极化干扰,严重影响系统的性能。研究表明,30 dB的天线极化隔离度,在恶劣天气情况下,最大可能是极化隔离度下降到10 dB左右。为了消除这种干扰,一般采用交叉极化干扰对消算法(XPIC)进行干扰消除[1-5]。
数字域上处理的XPIC算法结构一般有检前对消和检后对消两种方案。检前对消是对AD采样后的两路极化信号直接进行对消,不需要事先进行两路信号各自的载波同步、符号同步和符号检测等处理。检后对消则需要两路极化信号各自解调,完成符号检测后进行干扰对消。两者的在接收机的位置结构如图1所示。

图1 检前、检后对消位置关系
检前对消的优点是无需后续解调即可直接进行对消处理;而检后对消必须要求左、右旋两路极化信号解调的载波环和符号同步环路都正常锁定,才能进行对消处理。在较强交叉极化干扰时,若载波环和/或符号同步环无法锁定,检后对消将无法进行,导致接收机无法正常工作。此情况下先进行检前对消,便能使后面的环路锁定,并且有较好的误码性能。检后对消的优点是它是基于符号判决误差提取的,通过自适应滤波器结构,在接收机能够锁定的情况下,具有较好的误码性能,而检前对消虽然对强干扰有较大优势,但其性能比检后对消要稍差。
综合考虑基于检前和检后对消的优缺点,采用级联的检前和检后方案,既能抗强干扰(检前)又能具有较好的性能(检后)。目前,已经采用文献[1]的检前方案研制了高速设备,并在我国中继卫星无线测试链路上进行系统级测试,验证了检前方案的可行性和性能。为了进一步提高接收机灵敏度,本文对检后对消算法进行理论分析和仿真,以期后续研制检前、检后级联的XPIC高速接收机。
文章第1节介绍卫通信道交叉极化干扰信道模型;第2节建立自适应对消器的数学模型;第3节阐述高速算法的实现结构;第4节进行仿真结果分析,总结全文。
1 交叉极化干扰信道模型
在同频复用的正交双极化通信信道中,由于电离层去极化影响(法拉第旋转)、恶劣天气以及天线物理误差[3](非理想的OMT隔离),造成两路正交的极化信号不再正交而出现交叉极化干扰。交叉极化干扰通信信道模型[3]可以表示如下:
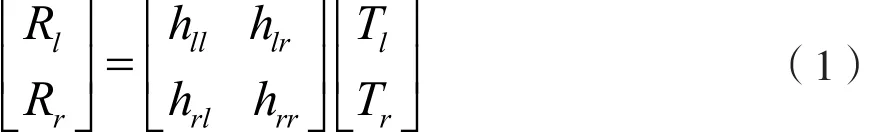
其中,Rl、Rr分别是接收机接收到的、被极化干扰的左、右旋信号;Tl、hll是发射机发射的正交左、右旋信号;hll、hlr、hrl、hrr分别是左、右旋收、发天线相应的信道传输增益(函数);基带形式的Rl、Rr、Tl、Tr一般按复数考虑。
定义交叉极化干扰的强度XPD(交叉极化隔离度)为:

其中,XPDl、XPDr分别是左、右旋信号中的干扰隔离度,其倒数即为极化干扰。根据信道的不同,XPD的取值在5~40dB,具体由传输无线信道、天线设备的理想情况及其他因素决定。
2 基于LMS的检后XPIC算法
消除交叉极化干扰的算法有多种,从数学模型式(1)可见,直接对干扰矩阵求逆,再与接收向量相乘,即可重构发射向量,消除交叉干扰:

算法的实现需要估计干扰矩阵中的hll、hlr、hrl、hrr四个参数。参数估计采用在发送波形中添加训练符号的数据辅助(DA)方法,也可以采用非数据辅助(NDA)的盲估计方法;而对消的实现可以在信号检测前实现,也可以在解调后进行。
文献[1-2]采用检前对消的方法,估计出干扰参数,并从信号中直接减扣干扰分量;文献[3-4]采用检后对消的方法。为了满足高速卫星通信高带宽利用率和自适应性,本文采用LMS算法的检后盲自适应XPIC对消算法,能够简化高速信号处理实现,并提高对消性能。
算法的实现框图如图2所示。这是对左旋信号进行干扰对消的结构示意图,而右旋分量对消与此相同。交叉干扰的左、右旋信号被A/D采样数字化后进行解调得到基带数据,左旋分量的自适应均衡结果叠加一个来自干扰分量的自适应滤波结果,两者叠加后送均衡器的判决和误差提取模块,通过这个误差分别调节均衡器的滤波器抽头系数和干扰支路的滤波器(对消自适应滤波器)抽头系数。由于自适应算法的作用,两个滤波器的系数调整会收敛到判决误差最小,算法思路与自适应均衡原理一致。
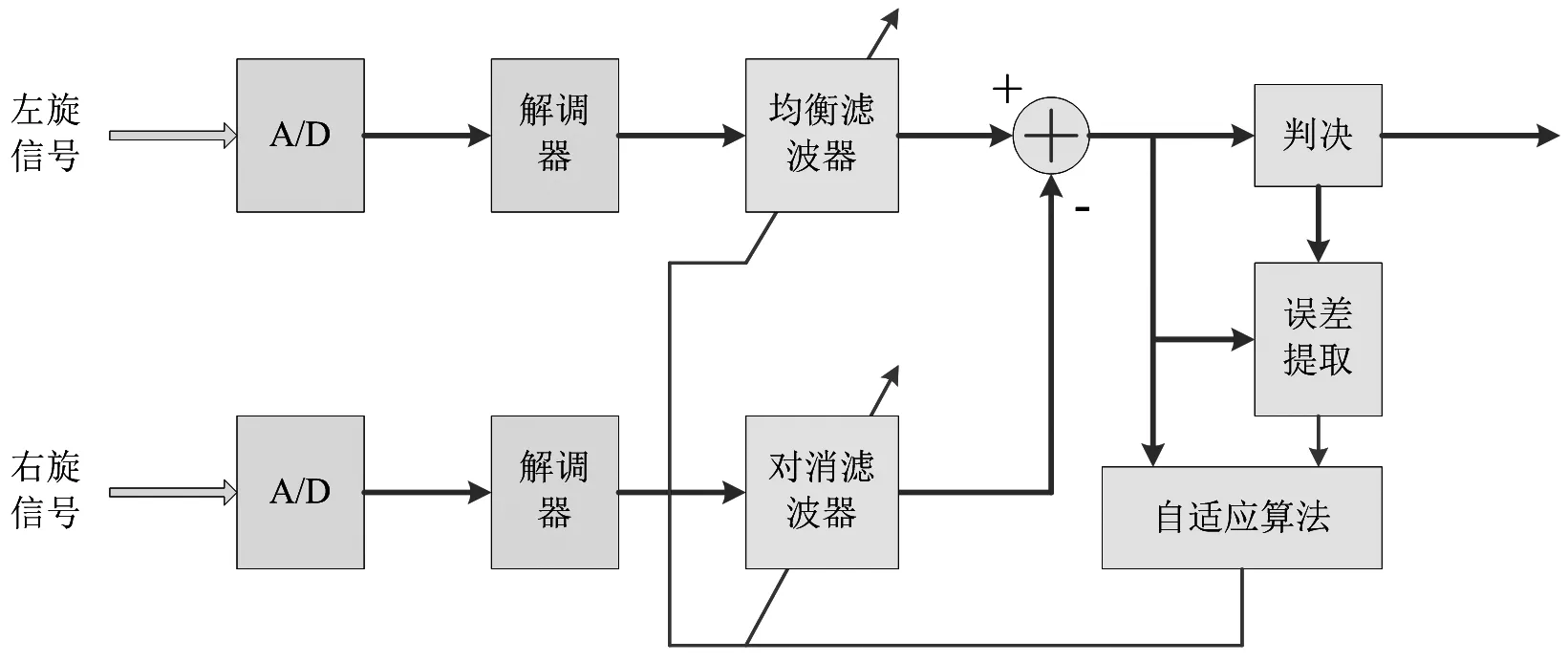
图2 检后盲自适应对消器结构
由于应用环境是传输速率处于吉比特每秒的高速卫星通信领域,通过对收敛速率和实现难度进行折中,选用LMS作为自适应算法进行抽头系数估计。
LMS算法是使均方误差E[e2(n)]=E[(d(n)-y(n))2]的期望值最小。LMS算法本质上是(随机)最陡下降算法,其梯度向量的真值由数据直接得到的估计来近似。同RLS算法相比,LMS算法的优点是计算简单,缺点是收敛速度较慢,需要几百个符号周期。但是,对高速数传而言,LMS算法的收敛速率对应用影响不大。
LMS算法的基本公式如下:
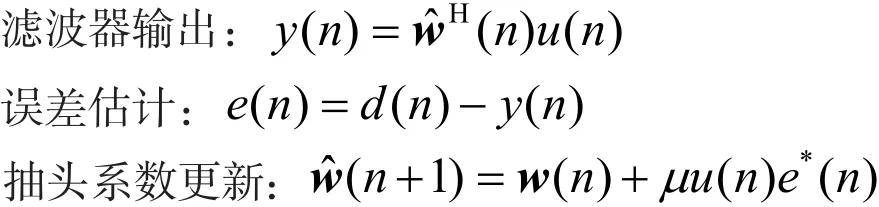
其中,d(n)是第n时刻的信号检测判决输出,y(n)是n时刻的均衡器输出,e(n)是误差,wˆ(n)是抽头系数矢量,μ是学习步长因子,u(n)是自适应滤波器权值矢量。
3 算法仿真及结果
利用介绍的对消算法,本节在Matlab软件环境中进行算法性能仿真。仿真的内容放在非理性接收的情况下,即存在载波、定时同步误差的情况下,极化对消器XPIC的理论性能曲线。
仿真对信噪比SNR变化、隔离度XPD变化以及存在多普勒和符号定时误差的非理想同步情况下的各种情况,进行独立仿真和联合仿真。仿真中,信号参数的变化范围如下:
(1)信噪比SNR:5~25 dB;
(2)隔离度XPD:5~20 dB,分为实干扰和复干扰;
(3)定时误差:-90°~90°;
(4)多普勒:相对于符号速率,从0.000 1%~0.01%;
(5)滤波器参数:9或25,对消和均衡滤波器采用相同阶数。
算法参数设定为:均衡器学习步长0.001、对消器学习步长0.000 5。
3.1 理想同步情况
理想同步情况下,信道参数为alpha=0.2+0.2i(有相差)。仿真SNR变化(扫描)和XPD扫描两种情况,结果如图3、图4所示。

图3 SNR扫描性仿真曲线

图4 XPD扫描性仿真曲线
图3 和图4给出了在SNR和XPD变化的情况下,均衡器和对消器在不同开关状态下得到的误码率相对关系。可见,XPIC干扰对消器效果明显。
3.2 存在定时偏差情况
定时偏差是指主通道和辅通道中对干扰信号定时(位同步)相位之间的偏差。本文采用半余弦波形(近似)内插,获取延迟符号进行仿真。为了便于建模,设一个符号内的相位延迟用

图5 仿真用符号半余弦波形模型
不同符号周期延迟和相位延迟的仿真结果,如图6、图7所示。
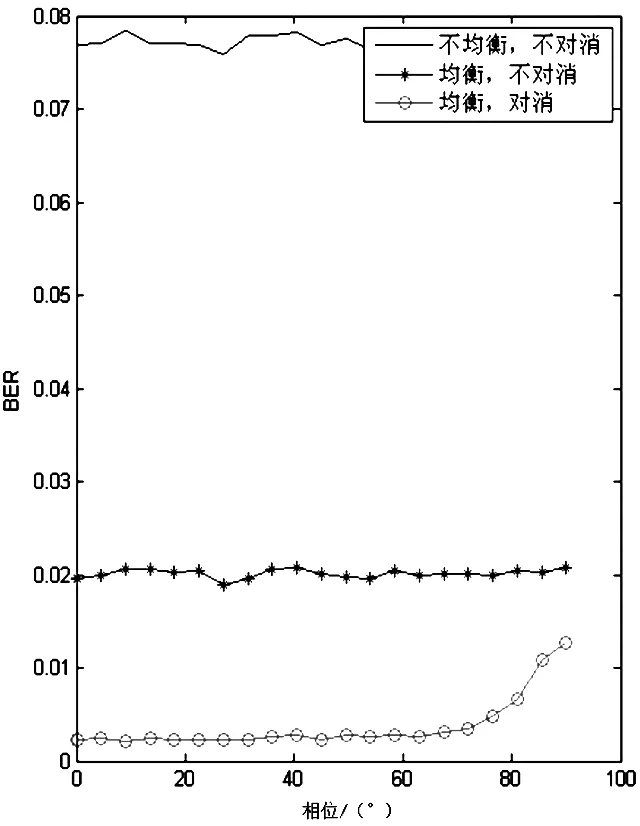
图6 2个符号偏差(信号中干扰延迟)

图7 7个符号偏差(信号中干扰延迟)
仿真结果显示,π/2之内的分数相位误差,以及小于滤波器阶数的整数倍符号移位,对性能影响不大;但超过滤波器阶数1/2以上的相位延迟,对性能影响较大,甚至使对消性能完全丧失。
3.3 存在多普勒的情况
两路信号中的干扰信号的码多普勒或者说符号频差,直接加在基带符号上。采用相对于码速率的0.05%~1%。本次仿真采用参数为:信噪比SNR为11 dB;相位无偏差;滤波器长度25阶。仿真结果如图8、图9所示。

图8 相对于符号速率的多普勒(步进0.05%)

图9 相对于符号速率的多普勒(步进0.000 1%)
可见,较大的多普勒对性能影响很大。当降低码多普勒到0.000 1%时,其影响可以忽略。因此,算法对码多普勒的要求相当高。
3.4 存在联合定时偏差及多普勒情况
联合定时误差和多普勒情况的仿真参数为:干扰参数为alpha_t=0.2+0.2i,信噪比SNR为11 dB;相位偏差(图10为0°~90°,图11为固定45°)、多普勒扫描范围(图10为固定0.001%,图11为0~0.03%),仿真结果如图10、图11所示。

图10 联合变化定时偏差和固定多普勒

图11 联合变化多普勒和固定定时偏差
可见,在组合情况下,多普勒的大小和定时误差大小对性能的影响是二者影响的叠加。
4 仿真结论
利用仿真结果可得到如下基本结论:
(1)理想同步情况下:①固定隔离度时,XPIC对消有效果,性能与信噪比成趋势变化,随着SNR的增加,对消性能逐渐提高,误码趋向于0;②固定信噪比时,XPIC对消有效果,稳定收敛,对消性能与SNR地板性能很接近,与无干扰情况下相同SNR的误码性能很接近。可见,理想情况下,XPIC性能较好。
(2)存在符号定时误差的情况下:①一个符号内定时误差小于70°,对性能无大影响;②对于多个符号整周期延迟,当延迟小于滤波器长度的1/2时,影响可以近似忽略。可见,符号定时对性能有影响。但是,符号内定时误差是个随机情况,无法保证小于70°(大于70°的概率为22.3%),可整周误差加长FIR阶数给予克服,但需硬件实现,要进行资源和复杂度考虑的折中。
(3)存在多普勒的情况下:①当两路中干扰信号的频差小于0.002%,如符号速率为300 MHz时,折算的多普勒小于6 kHz,多普勒影响可以忽略;②当大于0.002%后,多普勒影响逐渐加大,到0.06%后(300 MHz符号速率折算值为180 kHz),性能比均衡器还差;③增加抽头长度,性能没有改变。可见,多普勒对性能有影响。当小于符号速率的0.002%时,影响可以忽略;改变抽头长度也无影响。
(4)定时误差和多普勒联合作用的情况下:①仿真结果基本和两者单独作用是相同的,共同作用下有细微变化;②固定多普勒扫描相位时,受影响的相位角范围变大,从70°变为50°;③固定相位角,扫描多普勒时,与单扫多普勒,性能影响相对较小。可见,多普勒和相位角误差联合作用下,基本满足线性叠加性,存在一定的影响。
本文在前期检前对消器设备研制的基础上,为进一步提高XPIC的干扰对消性能,设计了基于LMS的自适应检后对消技术,并对其在理想情况下、存在多普勒误差和定时误差情况下的对消性能进行了比较仿真,给出了仿真结果。文中提出的检后对消技术和仿真的性能结果能为后续的算法研究、设计实现、设备研制与测试提供参考。
