在组合图形中探索面积问题——《圆的面积的拓展练习》教学设计与说明

安徽省合肥市合肥师范学院数学与统计学院 洪 倩

【教学内容】

苏教版《义务教育教科书·数学》五年级下册《圆》的增补内容。

【教学重难点】

重点：组合图形中圆面积的计算

难点：割补法求组合图形中圆的面积

【课前思考】

学生在学习完圆这一章节内容后已经可以熟练运用圆的面积公式S=πr2，然而例题简单而习题困难，仅仅这些是不足以解决问题的，特别是当碰到组合图形中圆的面积问题时大部分学生便束手无策。主要原因在于：无法将题目中所求的不规则图形进行拼凑、割补转变成规则图形。针对这一学生易错、常错且迫切需要解决的问题，有必要进行一次组合图形中圆面积问题的专项讲解。

【教学过程】

一、复习旧知，引出新课

1.复习旧知

师：同学们，我们学习了哪些图形的面积？（学生进行集体回答：圆、三角形、正方形、长方形、平行四边形、梯形）

师：这些图形的面积怎么求呢？（学生回答）

2.引出新课

师：我们已经知道简单图形面积的求法，但当我们遇到的图形并不是一个完整的圆，三角形、长方形等简单图形而是一个组合图形时，应该怎么办呢？

【设计意图：教师在复习旧知的基础上，进行提问，引出新课。】

二、分组讨论，观察探究

1.割补法求面积

师：同学们观察图1、图2、图3，怎样才能把散乱的阴影部分图形集合在一起？

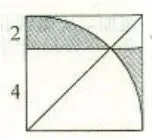
图1

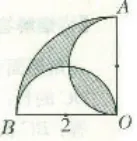
图2

（1）学生进行讨论，教师进行引导。

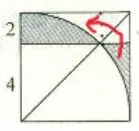
图4

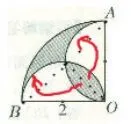
图5

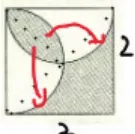
图6

（2）得出：

4×2=8 3.14×22÷4-2×2÷2=1.14 2×2÷2=2

2.等量代换法求面积

师：在图7中，直角三角形ABC的面积比半圆的面积多28平方厘米，阴影甲的面积为30平方厘米，直角三角形ABC和半圆面积的差与两个阴影部分面积的差有没有什么关系？

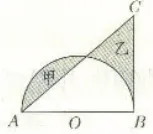
图7

（1）学生进行讨论

生：它们的差相同，因为如果同时从三角形ABC和半圆中挖去中间重合的空白部分，就相当于被减数和减数同时减去同一个数，差是不变的。师：能不能求出阴影乙的面积？

生：30+28=58（平方厘米）

（2）变式

师：现将题改为，图7中阴影乙的面积为比阴影甲的面积多28平方厘米，AB=40厘米，三角形ABC是直角三角形，求BC的长。

（3）教师引导，学生进行计算

S乙-S甲=28cm2

S三角形ABC-S半圆=28cm2

S半圆=3.14×202÷2=628（cm2）

S三角形ABC=638+28=666（cm²）

BC=666×2÷40=33.3（cm）

【设计意图：将题目进行变形，逐步深入，深化学生对等量代换求面积法的理解】

3.引辅助线法求面积

师：图8是由正方形和半圆组成的图形，其中P点为半圆的中点，Q点为正方形一边上的中点，那么阴影部分的面积是多少？（单位：厘米）

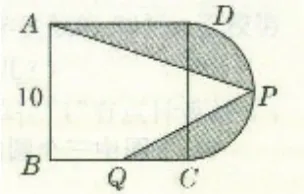
图8

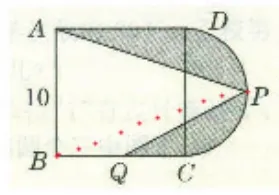
图9

学生分组讨论，进行思考。教师引导，得：连接PQ，S阴影=S正方形ABCD+ S半圆- S三角形APB- S三角形BPQ=10×10+3.14×5²÷2-10×15÷2-5×5÷2。

【设计意图：例举不同类型的组合图形的面积问题，拓展学生思维，化难为易，利于学生自我总结与反思】

三、回顾总结，留下问题

1.回顾总结

师：求组合图形的面积问题的方法并不仅限于此三类方法，在解决此类问题时应观察能否直接求阴影部分面积？如果不能，能否将阴影部分拼凑成规则图形？阴影部分面积之间有何关系？能否用辅助线划分成规则图形？能否进行平移、对称、旋转？

观察图形 → 进行计算

2.留下问题

师：请同学们自己仿照本节课所学内容，出3道与例题类似的题目进行练习。

【设计意图：让学生自己提出问题与解决问题，有利于学生深化理解本节课的知识，使之灵活化】