基于SK-CICA和Teager能量算子的滚动轴承故障诊断方法

安雪君，郝如江，史云林

(石家庄铁道大学 机械工程学院，石家庄 050043)

在强背景噪声下，滚动轴承发生早期故障时产生的信号往往会被堙没，这对长期进行高强度运转的设备造成了安全隐患，因此研究滚动轴承的早期状态监测和微弱故障诊断十分必要。

为在信号含噪的情况下有效提取滚动轴承微弱故障的特征频率，将谱峭度 (Spectral Kurtosis，SK)[1-2]与约束独立分量分析(Constrained Independent Component Analysis，CICA)[3-4]相结合进行信号的降噪及分离，并利用Teager能量算子(Teager Energy Operator，TEO)[5]突出振动信号中的冲击特征，识别出轴承故障。

1 SK-CICA算法基本理论

1.1 谱峭度法

峭度对冲击信号敏感，在故障诊断中常作为判断齿轮及轴承等振动冲击信号强弱的指标。但其受噪声的干扰较严重，并对冲击的变化情况不够敏感，为更有效地提取出信号中的瞬态信号成分，提出了谱峭度的概念，其定义为

(1)

式中：<·>和|·|分别表示取模和数学期望(平均值);H(t,f)为振动信号x(t)在频率f处的时频复包络，采用Fast Kurtogram求取[6]。

与短时Fourier变换相比，Fast Kurtogram算法的优点在于计算时间较短。该算法的主要步骤为：建立不同频带的1/3二叉树带通滤波器组，计算各子频带的谱峭度值并进行比较，从而自适应确定优化带通滤波参数，提取滤波包络信号[7]。

1.2 约束独立分量分析

CICA算法将源信号的先验知识作为约束函数(参考信号)，提取出与参考信号最相似的一个独立分量。基于源信号已知信息构造参考脉冲信号r(t)，将待提取的目标成分y和参考信号r(t)的距离函数定义为ε(y,r)，用以表示目标成分和参考信号的接近程度[8-9]。ε(y,r)可用均方误差ε(y,r)=E{(y-r)2}度量，CICA算法的数学模型为

目标函数

maxJ(y)≈ρ{E[G(y)]-E[G(v)]}2，

(2)

约束条件

(3)

式中：ρ为正常数；G(·) 为非线性函数；v为具有与y相同协方差矩阵的Gauss变量；ξ为阈值[10]。(3)式实际上是一个约束优化问题，通过Lagrange乘数法求解，可得到源信号的最佳估计，提取出目标源信号。

2 Teager能量算子解调基本理论

假设一个弹簧无阻尼振动系统质量为m，刚度为k，其运动方程为

x(t)=Acos(ωt+θ)，

(4)

式中：x(t)为质量块m相对平衡位置的位移；A为振动幅值；θ为初始相位；ω=(k/m)1/2为固有频率。

系统的瞬时总能量计算式为

(5)

将(4)式代入(5)式可得

ψ[x(t)]=ψ[Acos(ωt+φ)]=A2ω2。

(6)

分析以上公式，可见瞬时总能量和能量算子的差值为m/2，由此可以用能量算子来跟踪能量的变化[11-12]。瞬时幅值A与瞬时频率ω的平方积与瞬时总能量成正比，与传统的能量定义相比，Teager能量算子的定义突出了频率的平方，因此对于信号的瞬时能量变化具有更高的时间分辨率，有效增强了信号的瞬态冲击成分[13]。

3 基于SK-CICA和Teager能量算子解调的故障特征提取

基于SK-CICA的滚动轴承微弱故障诊断方法的流程如图1所示。首先将故障信号进行谱峭度分析，得到带通滤波优化参数后进行滤波处理，有效地削弱噪声影响；然后将其作为CICA的输入信号，提取出故障振动信号；最后利用Teager能量算子解调得到轴承的故障特征频率。

图1 故障特征提取方法流程图Fig.1 Flow chart of extraction method for fault feature

4 仿真分析

为了验证上述方法的有效性，构造故障轴承仿真信号(图2)进行分析：1)根据滚动轴承故障模型[14]建立仿真内圈故障的冲击响应, 故障特征频率f1为90 Hz，共振频率为3 000 Hz，采样频率为25 600 Hz；2)转频调制信号，调制频率f2为25 Hz；3)白噪声信号。

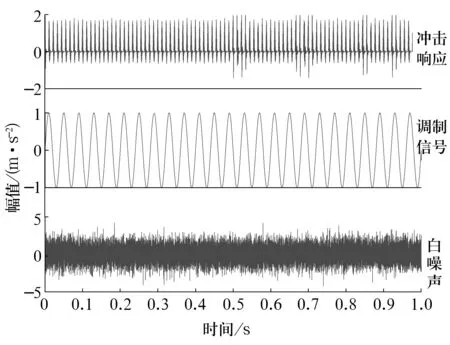
图2 仿真信号时域波形Fig.2 Time domain waveform of simulation signal

将图2中的3种信号混合并对其进行快速谱峭度图分析，结果如图3所示，得到带通滤波器的优化参数，即fc= 450 Hz，Δfc=100 Hz。基于CICA算法对信号进行线性混合，结果如图4所示；根据谱峭度计算的参数进行滤波处理后的信号如图5所示，可见部分噪声得到了削弱，冲击成分更加突出；将滤波后的3组信号作为CICA算法的输入信号S1，S2，S3，根据轴承内圈仿真故障频率90 Hz建立CICA的参考信号(图6)，分离结果如图6所示；对分离信号进行Teager能量解调分析得到的能量谱如图7所示，图中明显可见仿真轴承内圈故障频率90 Hz及其倍频，以及被转频调制后的边频，符合轴承内圈的故障特征。仿真试验结果表明，谱峭度与CICA算法结合，并经过Teager能量算子解调后可实现对轴承微弱故障的诊断。

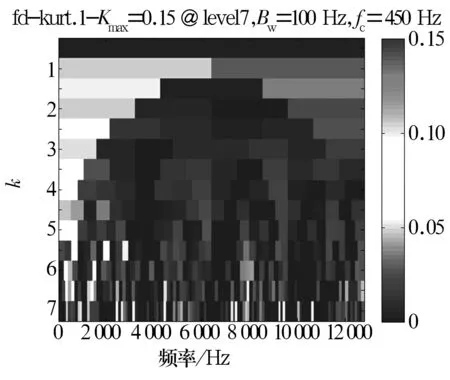
图3 混合信号快速谱峭度图Fig.3 Fast spectral kurtogram of mixed signal

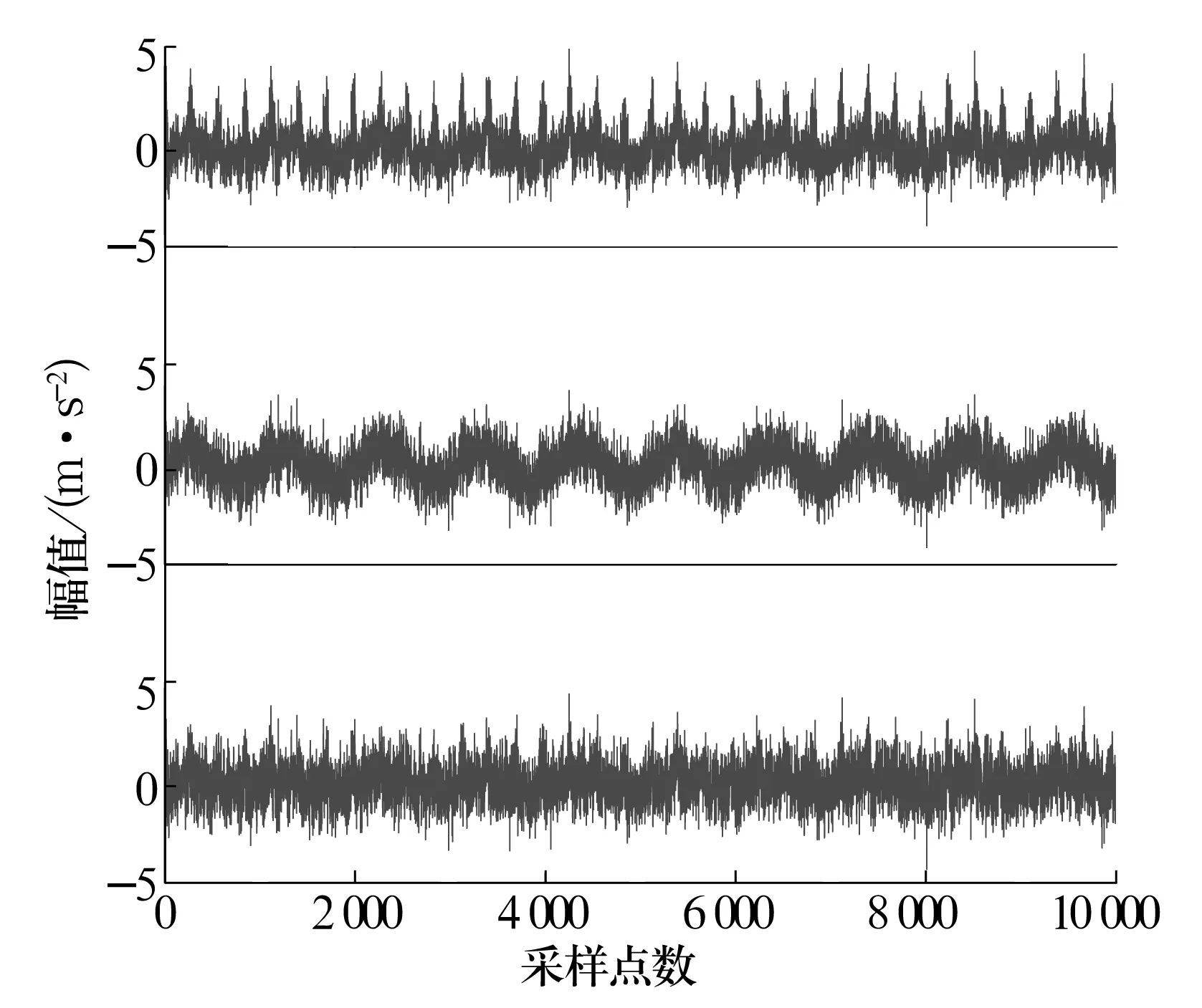
图4 混合信号时域波形Fig.4 Time domain waveform of mixed signal

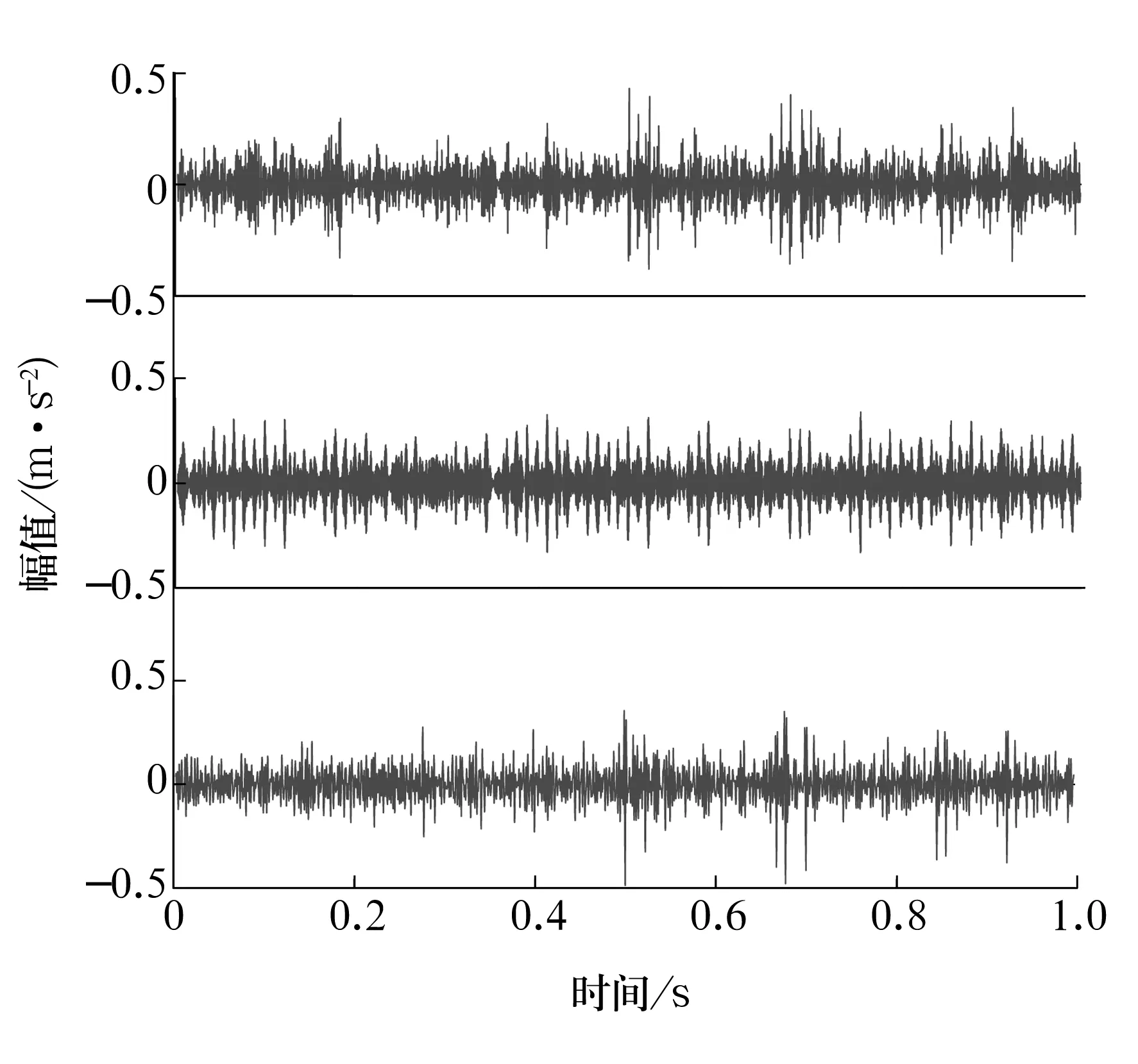
图5 滤波后信号时域波形Fig.5 Time domain waveform of filtered signal

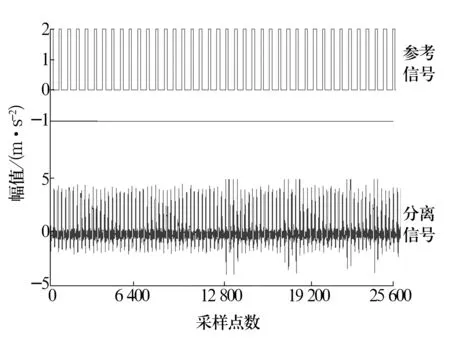
图6 参考信号和分离信号Fig.6 Reference signal and separated signal

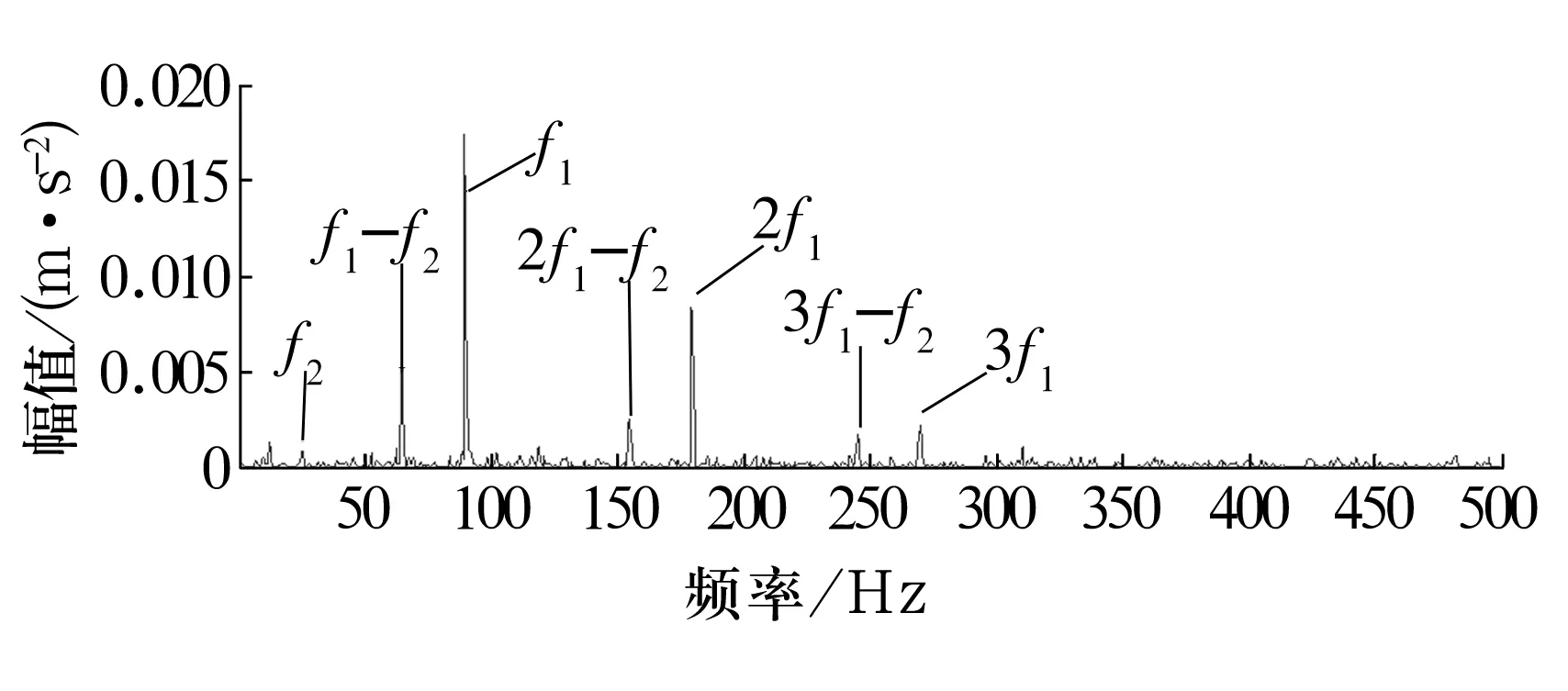
图7 Teager能量谱Fig.7 Teager energy spectrum

5 实际验证

为验证上述算法在实际应用中的可行性，通过故障诊断综合试验台进行滚动轴承内圈故障试验研究。该试验台的动力传动系统如图8所示，由1级行星齿轮箱、2级平行轴齿轮箱、轴承负载和可编程磁力制动器组成。故障轴承位于平行齿轮箱内的中间轴右侧(图9a)，双通道加速度传感器布置在靠近故障轴承的轴承座外壳上，分别位于径向和轴向，如图9b所示。电动机输入转速为2 400 r/min (即转频40 Hz)，传递到平行齿轮箱中间轴的转频为2.537 Hz。轴承型号为61800，其基本参数见表1，轴承内圈故障类型为早期磨损微弱故障。计算得到内圈故障特征频率为13.78 Hz。

图8 齿轮箱传动系统图Fig.8 Diagram of transmission system of gearbox

图9 故障轴承及传感器的安装位置Fig.9 Installation position of fault bearing and sensor

表1 故障轴承几何参数Tab.1 Geometric parameters of fault bearing

利用DASP数据采集仪采集数据，采样频率为25 600 Hz，数据长度为51 200个点。采集2个通道的数据，首先利用CICA算法对不做滤波处理数据进行盲源分离，根据该轴承的内圈故障频率理论值13.78 Hz建立参考脉冲信号，分离结果如图10所示，对分离出的信号做Hilbert包络谱分析，由于该齿轮箱结构较复杂，工作时除了噪声的影响，可能还存在其他结构的冲击干扰，从图11中可见包含的频率成分较复杂，其中平行齿轮箱的高速轴转频(理论值8.75 Hz)及其倍频干扰严重，轴承内圈故障频率几乎不可分辨，说明直接利用CICA算法对实测信号分离出的结果并不可靠，不能达到很好的故障提取效果。

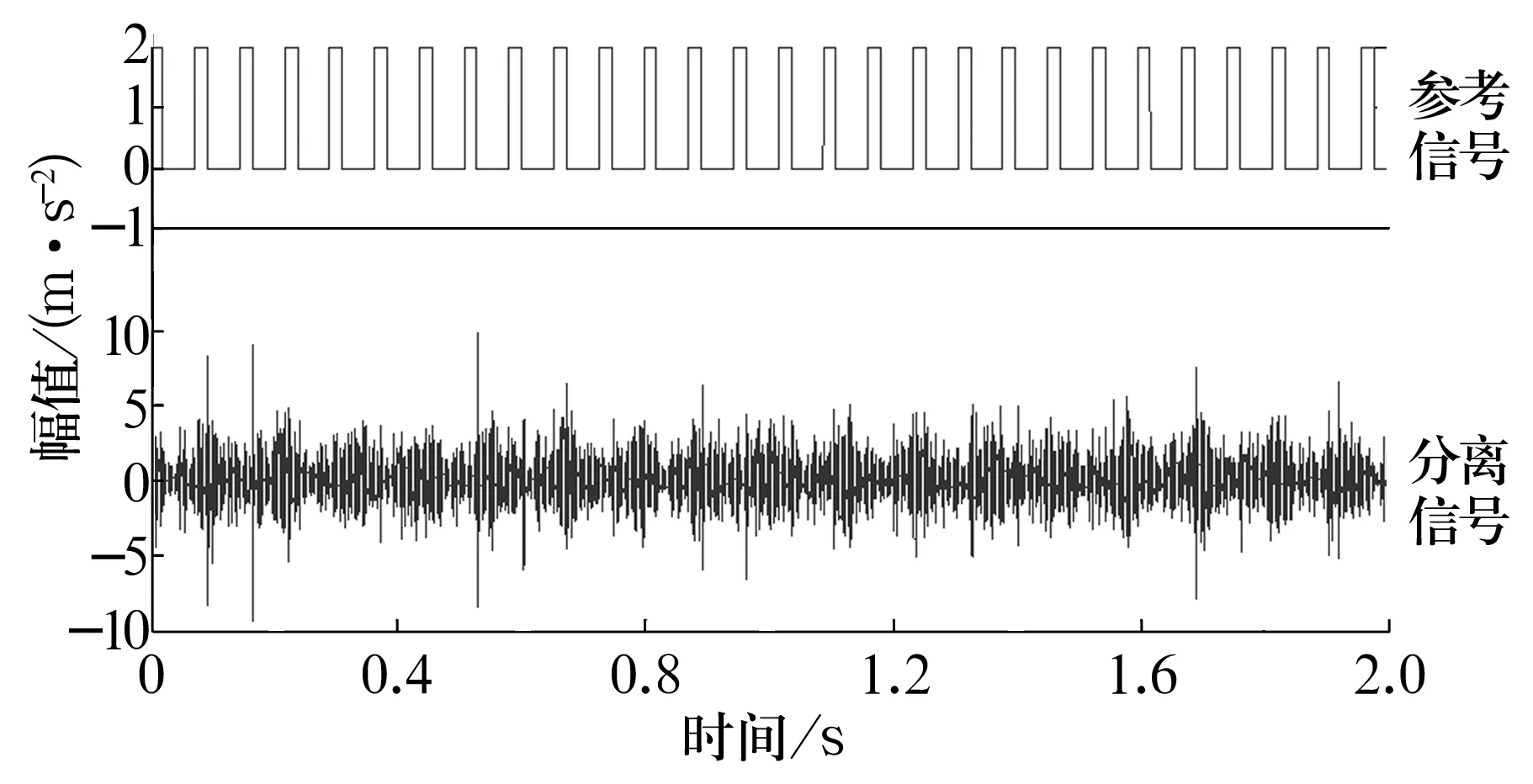
图10 未滤波信号CICA分离结果Fig.10 CICA separating result of unfiltered signal

图11 分离信号的Hilbert包络谱Fig.11 Hilbert envelope spectrum of separated signal

对原始两通道信号先进行谱峭度分析，结果如图12所示，分别得到优化滤波参数(fc1=7 400 Hz，Δfc1=400 Hz；fc2=9 800 Hz，Δfc2=400 Hz)，对两通道信号进行滤波，滤波后信号与原始信号的时域对比如图13所示，可见滤波达到了一定的降噪效果，冲击成分更加突出。

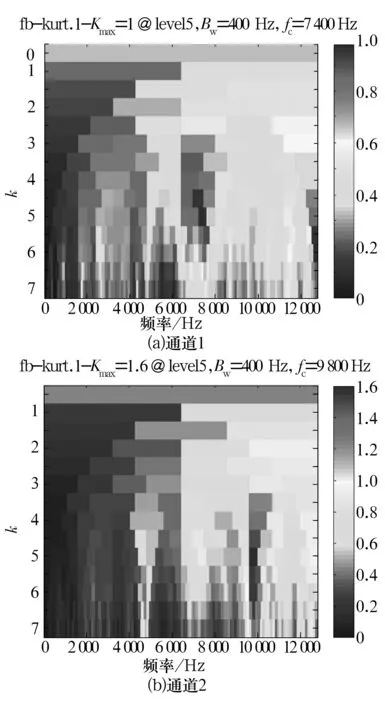
图12 原始信号的快速谱峭度图Fig.12 Fast spectral kurtogram of original signal

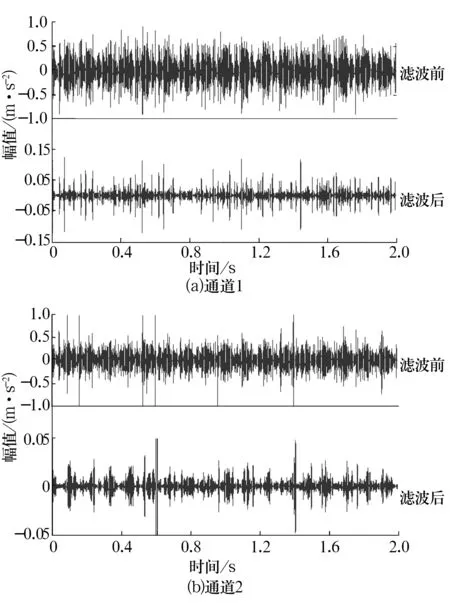
图13 滤波效果对比Fig.13 Comparison of filtering effect

将滤波后的2个信号输入到CICA算法中，得到的CICA分离信号及其Teager能量谱如图14所示。与图11中原信号的Hilbert包络谱对比可知，图14b可明显分辨出轴承内圈故障频率(理论值13.78 Hz)及其倍频成分，证明了SK-CICA结合算法以及Teager能量算子解调在轴承微弱故障特征提取方面的优越性。

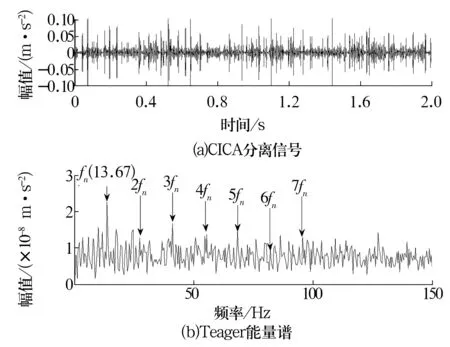
图14 分离信号及其Teager能量谱Fig.14 Separated signal and its Teager energy spectrum

6 结束语

SK-CICA算法将谱峭度算法的自适应滤波能力与CICA算法的信号提取技术优势互补，实现了对混合信号的降噪和故障信号的提取；Teager能量算子解调算法有效增强了信号中的冲击成分，与传统的Hilbert包络解调算法相比更具有优越性。适用于机械设备中轴承的早期微弱故障诊断，具有良好的工程实际应用前景。