基于集成AGNES & GA算法的深沟球轴承套圈订制优化
2018-07-25许林明杨晓英张志文
许林明,杨晓英,2,张志文
(1.河南科技大学 机电工程学院,河南 洛阳 471003;2.机械装备先进制造河南省协同创新中心,河南 洛阳 471003)
深沟球轴承套圈订制是指根据轴承的径向游隙技术要求,将数量不配套的在库内(外)圈定制出与其合套的外(内)圈的过程。在轴承装配过程中,当套圈零件库存不能满足装配计划需求时,需要根据现有库存套圈以及技术要求进行订制生产。订制生产可以避免按工艺生产的盲目性,减少生产批量,从而减少零件库存,提高合套成功率。目前轴承企业在对套圈订制时,是根据工人经验将库存套圈偏差值分段和球组合进行订制,其订制结果往往和工人的能力有很大关系,主观因素明显,容易造成订制结果离散程度较大,给后续生产带来困难。如果严格要求订制偏差,则严重降低生产效率,延长了生产周期;如果追求生产效率,放宽对订制偏差的要求,则容易导致生产的零件不符合订制要求,最终造成废品率高,增加生产成本。因此,在对套圈订制时,需要用科学的方法对套圈订制进行优化,以实现轴承订制生产的低成本、高效率运行,同时使订制结果聚集程度最高,便于后续加工生产。
目前国内外关于轴承套圈订制的研究较少,文献[1]阐述了轴承游隙的选配方法及最大匹配原理,并采用VB与MATLAB混合编程实现了轴承游隙的自动选配及内外圈匹配数量最大;文献[2-3]运用网络流规划将该问题转化为网络最大流问题,并建立了一种选配模型;文献[4]针对有限元分析在选择装配运算中的不足,提出元模型和粒子群优化算法相结合的混合算法;文献[5]提出一种基于强弱Pareto进化算法2(SPEA2)的复杂产品多目标、多质量要求下的选择装配方法,以装配精度和装配率作为质量要求的评价方式,建立了多质量要求下的选择装配模型;文献[6]采用分组的策略对复杂产品的零件进行选择装配,应用模糊进化的算法优化装配过程;文献[7]提出了面向任务的多传感器资源预先分配问题,建立了多传感器资源预分配数学模型,然后利用改进匈牙利算法结合3种任务下的目标函数进行了求解;文献[8]针对机械产品多质量要求下的选配问题,提出一种基于强弱Pareto和遗传算法的多质量要求下的选择装配方法。
订制作为一种组合优化问题,遗传算法(Genetic Algorithm)是其常用的工具。遗传算法作为一种启发式智能搜索算法,相关研究成果较多:文献[9]针对传统遗传算法早熟收敛和收敛速度慢的问题,提出一种双精英协同进化遗传算法(Double Elite Coevolutionary Genetic Algorithm, DECGA);文献[10]提出一种自适应遗传算法和爬山算法相结合的改进算法HCGA;文献[11]提出一种自适应定向突变算子,通过结合定向局部搜索策略和自适应随机搜索策略提高了算法的全局搜索能力和收敛速度;文献[12]提出基于混合遗传算法的均匀设计,并利用反向搜索策略进行局部搜索;凝聚层次聚类算法[13-15]是一种自底向上,首先将每个对象作为一个簇,然后合并这些原始簇为更大的簇,直到满足终止条件,常用于数据挖掘。现有研究成果涉及轴承套圈订制的优化研究很少见,因此基于集成AGNES & GA 算法的深沟球轴承套圈订制优化进行研究,以订制后套圈沟道尺寸偏差段数量最小化为优化目标,以轴承径向游隙和球库存数量为约束条件建立套圈订制优化模型,采用凝聚层次聚类算法(AGNES)对套圈偏差值进行偏差段数量数据挖掘,基于改进型遗传算法进行订制优化。
1 问题与目标
深沟球轴承套圈订制问题描述为:轴承装配过程中已知内(外)圈零件库存信息、球信息以及径向游隙技术要求,而缺少与其相配套的外(内)圈库存,为了满足装配计划要求,需要根据现有内(外)圈零件库存信息来订制生产外(内)圈。
深沟球轴承径向游隙为Gr,外圈沟道直径为De,内圈沟道直径为di,球径为Dw。径向游隙及径向游隙偏差[16]为
Gr=De-di-2Dw,
(1)
Grm=ΔDe-Δdi-2ΔDw,
(2)
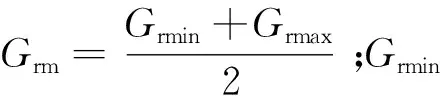
订制优化的目标:最大限度地提高订制生产效率、准确率,降低内外圈库存,要求订制后外(内)圈零件的尺寸偏差聚集程度最高,即订制后套圈偏差段分段数量最少。
2 优化建模
参数设定:设球径偏差种类为m,第j(j∈m)种直径偏差球能装出GSj套轴承;a表示事先按照工艺要求规定好的偏差段长度;设在库轴承套圈沟道尺寸偏差有n种,第k(k∈n)种尺寸偏差内零件个数为sk;Q为参与订制的套圈总数量;第k种尺寸偏差的套圈和第j种偏差的球匹配时,xkj=1,否则,xkj=0;SL表示订制后套圈沟道尺寸偏差段数量,最终目标是得出SL最小时的最优组合。
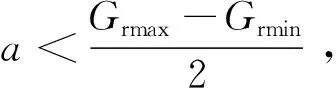
综上建立优化模型如下:
minSL,
(3)
约束条件为
3 集成优化算法
考虑到该模型是一种组合优化问题,同时需要对套圈沟道尺寸偏差段进行数据挖掘以得到尺寸偏差段数。因此,首先采用凝聚层次聚类算法对个体进行数据挖掘,得到个体的尺寸偏差段数,以此为基础构建个体适应度函数,然后再利用改进型遗传算法求解。
3.1 基于凝聚层次聚类算法的个体偏差段SL数据挖掘
采用凝聚层次聚类算法对某个个体进行数据挖掘,计算目标函数值SLi的具体流程如图1所示。凝聚层次聚类步骤为:
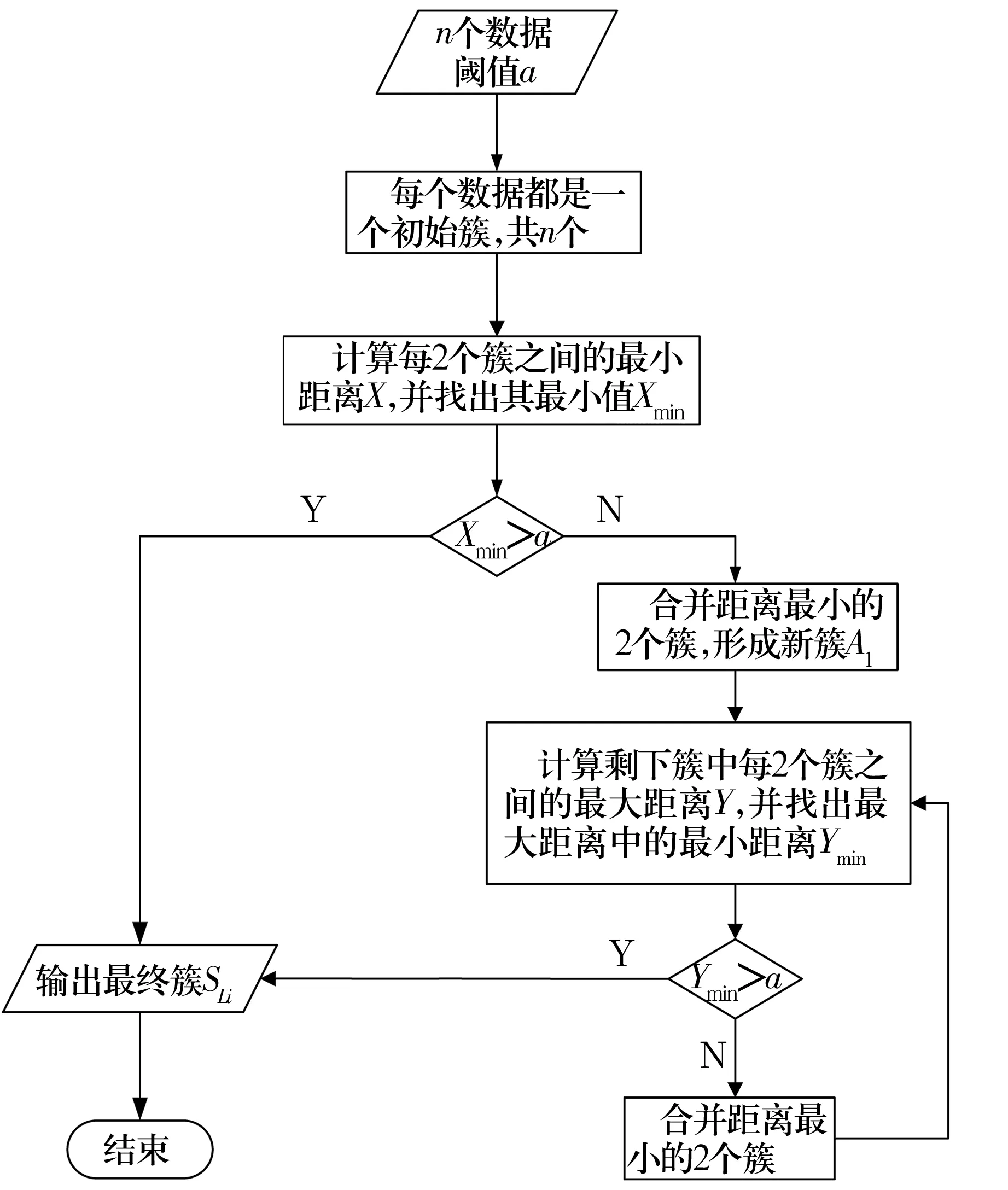
图1 基于AGNES的SL数据挖掘流程图Fig.1 Flow chart of data mining for SL based on AGNES
1)将n种套圈沟道尺寸偏差中的每一种偏差单独作为一个独立的簇;
2)规定阈值a,以套圈尺寸偏差段区间长度(按照工艺规定)作为阈值;
3)找出每两个簇之间的最小距离Xmin,若Xmin≤a,则合并这2个簇,接着进行下一步骤,若Xmin>a,则直接输出最终簇;
4)计算剩下每两簇之间的最大距离Y,并找出其中的最小值Ymin,若Ymin≤a,则合并这2个簇,若Ymin>a,则直接输出最终簇;
5)重复步骤3,4,直到簇之间距离大于阈值a;
3.2 基于改进型遗传算法的开订制优化
遗传算法[17]是由美国Holland教授于1975年提出,其尤其适用于处理传统搜索方法难于解决的复杂和非线性问题,可广泛用于组合优化、机器学习、自适应控制等领域。传统遗传算法容易陷入局部最优解,因此,将局部搜索能力强的2-Opt(2-Optimization)算法[18-19]与遗传算法相结合以提高其局部搜索能力,同时针对传统遗传算法的收敛速度慢、算法稳定性差问题,提出自适应交叉变异概率予以弥补。
3.2.1 染色体的编码方式
根据上述模型以及轴承订制特点,最终选用矩阵形式来表征个体染色体,2×n的矩阵第1行为套圈沟道尺寸偏差,第2行为球径尺寸偏差。因每种偏差的球都有数量限制,因此在订制时,所使用每种偏差的球都不得超过其库存数量,用矩阵M表示为
(9)
式中:Δxn为套圈沟道尺寸偏差值;ΔDwyj为随机从所给的球中选择一种,且满足(7)式。
3.2.2 适应度评价
采用凝聚层次聚类算法对某个个体进行优劣性评价时,根据所给定阈值,对每个个体进行聚类操作,由该个体最终簇的数量作为评价依据,簇的数量越少,则表明该个体的生存能力越强;反之,表明该个体越差。
个体的适应度函数为
fi=1/SLi,
心有静气,才能客观看待人事,沉着思考问题。反之,心有怒气,整个人就会沦为情绪的奴隶,辨不清是非真假,自然容易出乱子。
(10)
式中:SLi为个体聚类后簇的数量。
3.2.3 选择操作
假设种群大小为N,采用最优个体保留策略,在每次迭代后保留种群中适应度值最大的个体,使其直接进入到下一次迭代,将剩下的N-1个个体利用轮盘赌的方式生成N-1个个体。该方法能够保证最优个体遗传给下一代,同时也保证了适应度大的有较高机会进入下一次迭代。
为了克服固定交叉率和变异率所导致的收敛速度慢、算法稳定性差以及早熟等问题,提出自适应遗传算法,对遗传控制参数Pc和Pm进行自适应调整[20]。同时,为了保证最优个体不被破坏,采用最优保存策略,直接将最优个体复制到下一代。
(11)
(12)
Pc1=0.9,Pc2=0.6,Pm1=0.1,Pm2=0.001。
式中:fmax为群体中最大的适应度值;favg为每代群体中的平均适应度值;f′为要交叉的2个个体中较大的适应度值;f为要变异个体的适应度值。
3.2.4 交叉操作
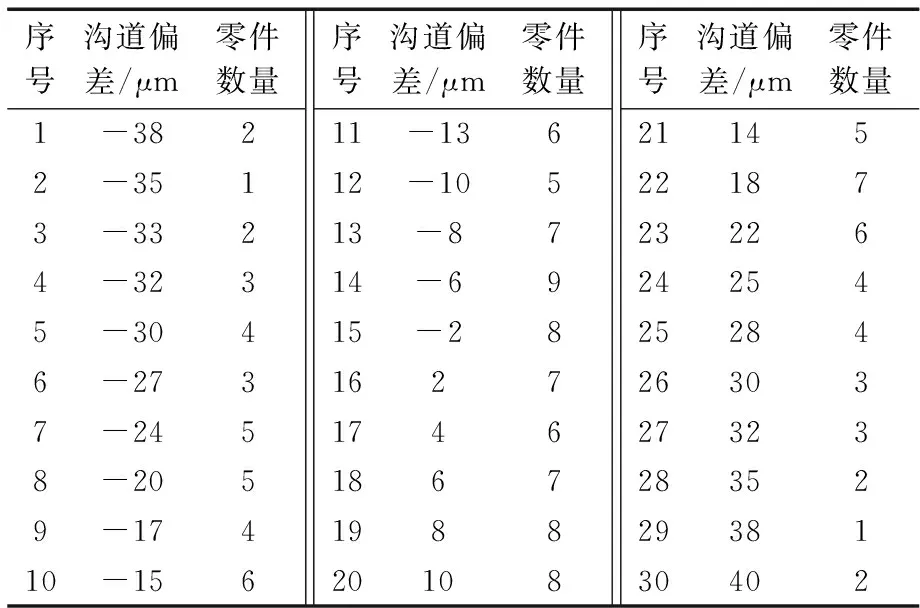
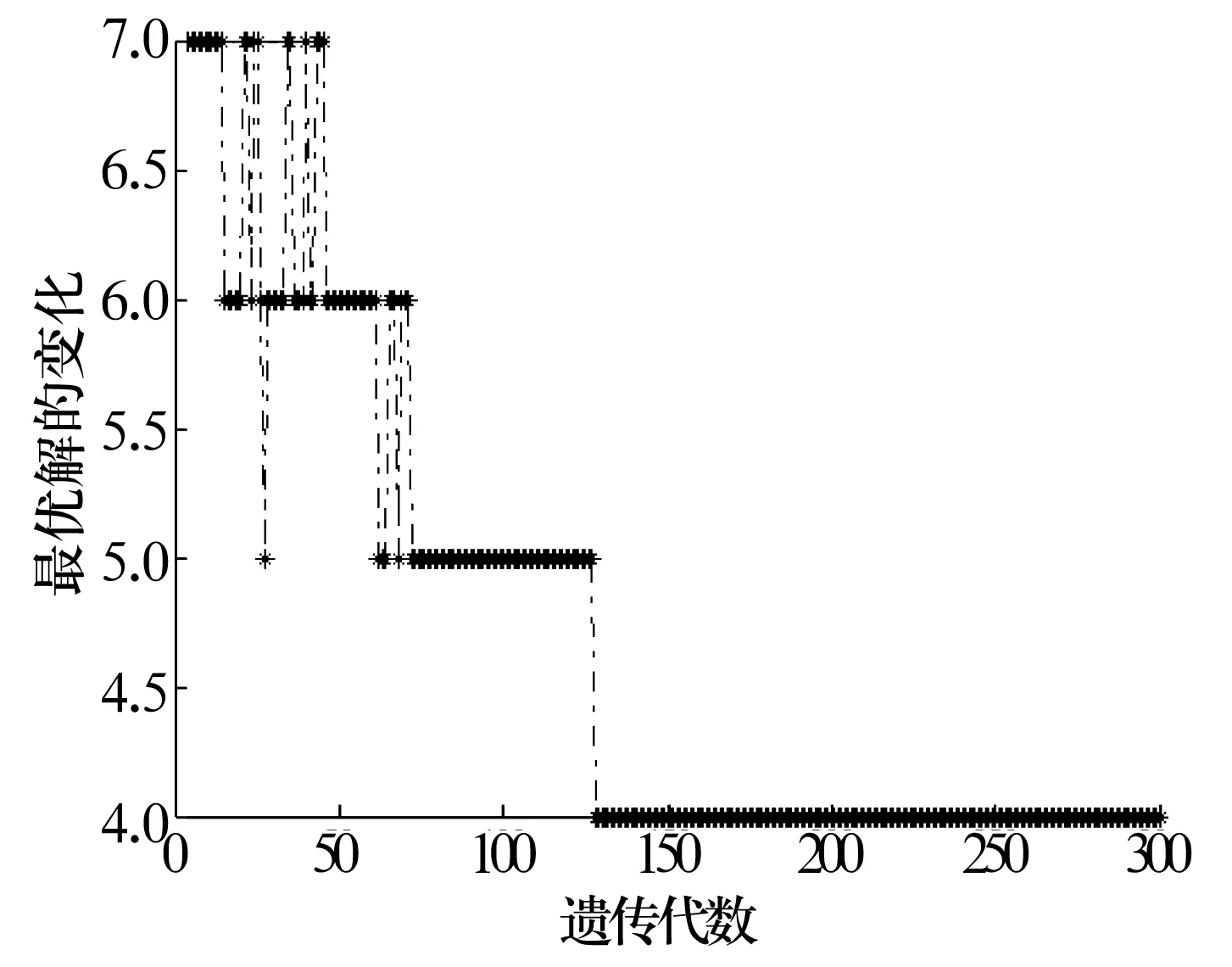
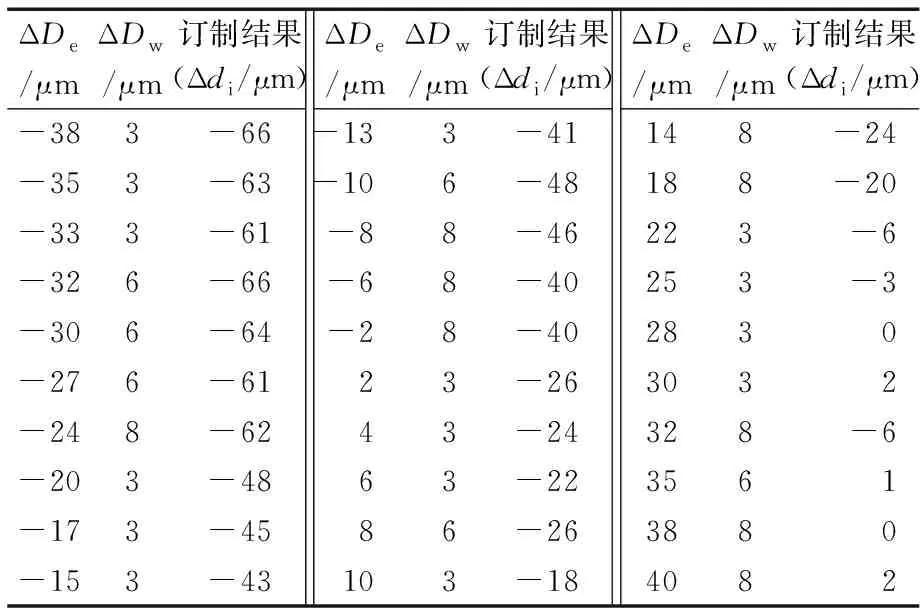
根据自适应交叉概率Pc,当rand(1) 注意,在交叉时要满足以下2个约束: 1)为保证种群多样性,若两交叉点之间的父代基因相同,则重新进行交叉点的选择; 2)交叉后要满足(7)式的约束条件,若交叉后不能满足(7)式约束,则通过调整相关的不满足因子,使其满足要求。 3.2.5 变异操作 为保证种群的多样性,对父代个体以自适应变异概率Pm进行变异操作,当rand(1) 进行变异操作时也需满足约束: 1)如果新形成的个体在父代中已存在,则重新进行变异操作,直到形成全新的个体; 2)变异后要满足(7)式的约束条件。 3.2.6 2-Opt置换操作 为了弥补遗传算法局部搜索能力弱的缺陷,对每次进化后群体中的适应度最大的个体实施2-Opt置换算法,即随机选取染色体中2个点i和k,染色体第2行i之前和k之后的序列不变,将i到k之间的序列翻转其编号形成新的个体。并判断每次实施2-Opt置换算法后个体适应度值是否增加,若实施2-Opt后个体适应度值增加,则替换掉原个体,否则继续执行2-Opt置换操作,直到达到一定操作次数为止。具体算法流程如图2所示。 图2 基于改进型遗传算法的订制优化Fig.2 Customized optimization based on improved genetic algorithm 以深沟球轴承套圈订制为例,验证套圈订制优化模型和算法的有效性。规定径向游隙Grm为22 μm,可使用球径尺寸偏差ΔDw为3,6,8 μm(由于球数较多,在此不考虑球数的限制),库存外圈沟道尺寸偏差值见表1。 表1 外圈沟道尺寸偏差值ΔDeTab.1 Dimension deviation of outer ring raceway ΔDe 采用MATLAB 2013a进行计算,具体采用的遗传控制参数有:种群规模为50,最大迭代次数为300次,聚类算法的阈值设置为8 μm。最终计算结果如图3所示,最优匹配结果见表2。 图3 内圈沟道尺寸偏差段数变化趋势图Fig.3 Variation trend diagram of dimension deviation segments of inner ring raceway 表2 最优匹配结果Tab.2 Optimal matching results 由图3可知,最初的内圈沟道尺寸偏差段数为7,随着迭代的进行,内圈偏差段数逐渐减少,当迭代到130次时达到最优,此时需订制的内圈偏差段数为4。由表2可知,最终内圈沟道尺寸偏差段分段情况见表3。 表3 偏差段分布情况Tab.3 Distribution situation of deviation segments 通过订制优化研究,大大减少了零件库存,预计生产批量可降低40%,同时提高了订制生产的准确性。 基于集成AGNES & GA 算法的深沟球轴承套圈订制优化方法,以订制后套圈沟道尺寸偏差段数量最小化为优化目标,以轴承径向游隙技术要求和球库存数量为主要约束条件,建立套圈订制优化模型,采用AGNES对套圈偏差值进行数据挖掘得出偏差段数量SL,以此为基础,建立适应度函数。采用改进型遗传算法进行优化搜索,并对每次进化后群体中适应度值最大的个体实施2-Opt置换操作以提高遗传算法的局部搜索能力。利用自适应交叉概率和变异概率,既保证了种群的多样性,又保证了算法的收敛性。通过实例应用表明了所提模型和算法能很好地契合深沟球轴承订制要求,提高了订制效率和准确率,降低了零件库存,减少了生产批量,为企业订制优化生产研究提供了一种有效的理论和方法。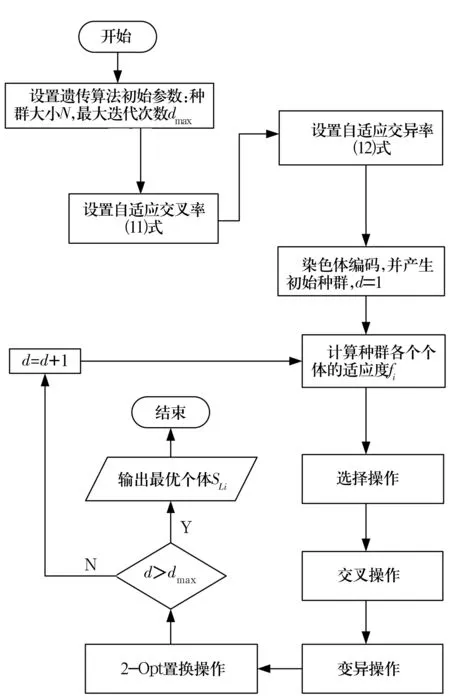
4 实例验证

5 结束语
