信道噪声实时产生算法及改进研究

杨志强 朱秋明,2, 台 鑫 刘 亮 陈小敏 廖志忠

(1. 南京航空航天大学电子信息工程学院，江苏南京 211100；2. 英国赫瑞瓦特大学工程与物理科学学院，爱丁堡 EH14 4AS；3. 中国空空导弹研究院，河南洛阳 471009； 4. 中国电子科技集团公司第41研究所,山东青岛 233006)

1 引言

无线信号在信道中传播必然受到各种噪声的干扰，进而影响接收机信号接收的准确性。研究不同传播环境下噪声对接收信号的影响，对无线通信系统的方案设计和性能评估必不可少。同时，如何在实验室环境下精确产生不同干扰噪声，从而用于真实模拟噪声对实际通信设备的影响变得越来越重要。鉴于实际中大部分噪声服从高斯分布，因此如何产生统计特性好，尾巴精确度高和重复周期长的高斯噪声是近年来通信测试领域的研究重点之一[1-3]。

经典的高斯噪声模拟方法有基于逆变换的方法[5- 6]和基于舍弃的方法[7- 8]。需要指出的是，逆变换方法和舍弃法为非均匀随机变量的通用产生方法，可以产生统计精确的高斯噪声，但是硬件实现比较复杂。

中心极限理论方法是高斯随机变量的特有产生方法，输出统计特性略差，但原理简单且易于硬件实现[9-10]。谐波叠加(SoS，Sum of Sinusoids)方法[11-12]是中心极限理论方法的一种改进，已被广泛应用于无线信道衰落的实时模拟。文献[13]基于SoS方法提出一种非平稳的莱斯衰落信道的仿真方法；文献[14]结合FPGA硬件平台，利用SoS方法实现了复合衰落的实时模拟；文献[15]则基于SoS方法提出了瑞利衰落场景下的非平稳MIMO信道衰落的实时仿真方法。需要指出的是，SoS方法不仅实现简单灵活，而且还可以产生各种高斯色噪声。本文基于课题组前期无线信道衰落模拟的研究基础，提出基于SoS的方法产生高斯随机变量，并借鉴Hadamard矩阵变换的思想将SoS方法产生的多路独立高斯随机变量进行线性叠加，获得统计性能更好、经过周期扩展的高斯噪声，更加符合信道噪声模拟的要求。

2 高斯噪声模型及特性

高斯噪声的幅值统计分布服从高斯分布，其概率密度函数(Probability Density Function，PDF)可表示为

(1)

式中，μ为均值，σ为标准差。当μ=0、σ=1时，该分布称为标准高斯分布，即

(2)

对应的累积分布函数为

(3)

其中，erf(·)表示误差函数。

图1(a)为标准PDF及其CDF的数值仿真曲线，考虑到精确的高斯仿真要求能够精确覆盖极低概率出现的区域，称为尾巴精确度，用标准差σ来衡量[16]。我们利用对数形式给出了PDF曲线，如图1(b)所示，该曲线可以清晰的展现尾巴区域的分布特性，如图中阴影区域。实际中考虑到硬件模拟的条件及需求，一般要求硬件模拟信道噪声的尾巴精确度达到3σ～5σ。

图1 标准高斯PDF及CDP曲线Fig.1 Standard Gaussian PDF and CDF curves

3 SoS产生方法及改进

3.1 SoS原理

逆变换方法和舍弃法比较适合软件仿真产生高斯随机变量，而硬件实现比较复杂。中心极限理论方法是高斯随机变量特有的产生方法，输出统计特性略逊于前两类，但原理简单且易于硬件实现。SoS方法是中心极限理论方法的一种改进，已被广泛应用于无线信道衰落的实时模拟[13-15]，该方法实现原理如下

(4)

其中，N表示散射支路数目；fn表示各谐波频率，φn表示各散射支路随机分布的初始相位。则当模型参数确定后，fn、φn为非零常数，而t可看成服从均匀分布的随机变量。

由SoS方法可知，第n支路加权谐波可表示为

(5)

(6)

(7)

(8)

当散射支路数N→时，根据文献[18]可知

(9)

将式(9)代入式(8)中，并运用文献[18]可得

(10)

因此，当N→时，SoS方法输出变量的瞬时幅度服从均值为0，方差为1的高斯分布。

3.2 基于Hadamard矩阵的改进

由于SoS方法输出各支路为周期波形，因而叠加后产生的高斯随机变量的周期为

(11)

式中，gcd(·)为表示各谐波频率的最大公约数。利用可编程逻辑器件(Field-Programmable Gate Array，FPGA)硬件实现时，采用定点余弦查找表产生各支路谐波，此时，余弦表位宽Wcos、深度Dcos定点化角频率位宽Dω对输出序列的周期会产生影响，根据文献[14]可知，当2Dω>Dcos时，最终输出序列的周期为

(12)

式中，ωi,i=1,2,…,N为谐波频率定点化的结果。由于随机变量重复周期较短，与真实环境下的信道噪声不相匹配，且由于各谐波的加权系数相同，容易造成统计特性的整体偏差。

为了尽可能地模拟真实信道环境下的噪声，本文借鉴Hadamard矩阵变换思想对传统的SoS方法进行改进，改善输出噪声的统计特性和扩展输出噪声的周期。设M行独立同分布高斯随机变量为

X=[x1,x2,…,xM]T

(13)

Hadamard矩阵为

H=[hi, j]M×M

(14)

为了减少硬件实现的复杂度，令H的元素为±1，且满足

(15)

经过Hadamard矩阵变换输出的M行高斯随机变量为

Y=[y1,y2,…,yM]T

(16)

三者满足如下关系：

(17)

一旦矩阵H确定，则Y与X的关系就确定，yi与xi满足以下关系

(18)

矩阵变换过程输出为

(19)

本文采用SoS方法实时产生M行独立同分布高斯随机变量代替预存式的高斯随机变量，每个高斯随机变量由N路谐波叠加，MN个谐波的频率各不相同，则矩阵变换后输出的高斯随机变量的周期可表示为

(20)

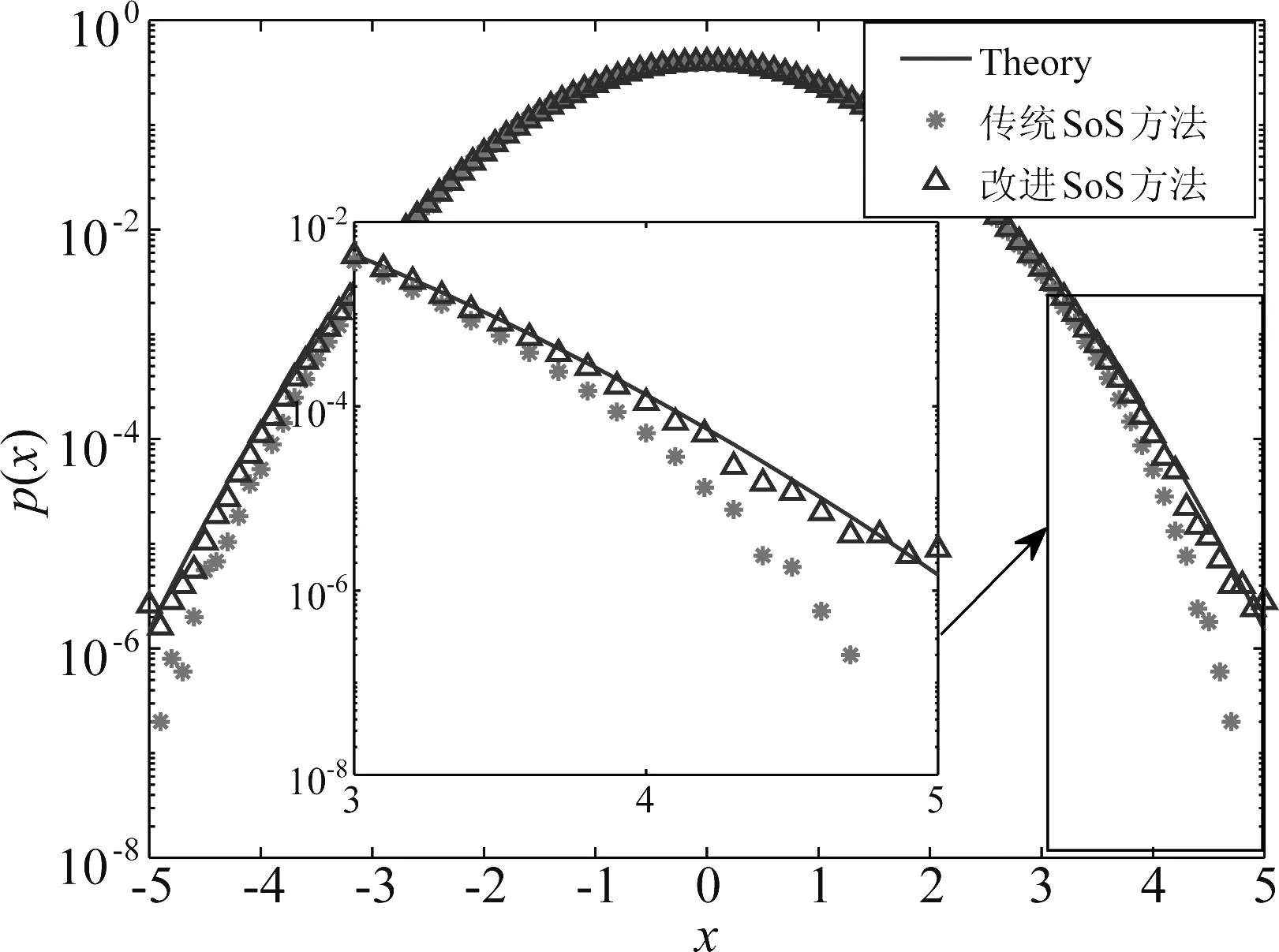
本文每隔τ,τ

(21)

式(21)的结果可看作是M行独立同分布高斯随机变量的线性叠加，此方法避免了矩阵变换过程导致各行高斯变量之间独立性变差，可以改善输出噪声的统计特性，同时又能扩展输出噪声的周期，其周期远远大于式(20)给出的周期。

4 数值仿真及分析

为了验证本文SoS改进方法产生高斯随机噪声的性能，我们设定N分别为4，16，64，并利用上述方法进行仿真，输出数据长度为108。实际输出高斯噪声序列的统计幅值分布如图2所示，从图可以看出，当N很小时，幅值统计分布与理论高斯分布之间的误差较大，尾巴精确度较低，当N增大时，两者之间的误差变小，且尾巴精确度提高，当N→时，输出噪声的幅值统计分布趋向理论高斯分布。图3则仿真比较了改进前后两种方法输出的幅值统计性能，仿真中假设每路SoS方法的谐波数目为16，共产生4路独立同分布的高斯噪声，仿真输出数据长度为108。从图可以看出，改进后方法的幅值统计分布性能优于传统SoS方法，尾巴精确度也有所提高。

图2 不同N时的幅值统计分布Fig.2 Statistical distribution of amplitude at different N

图3 传统与改进SoS方法统计分布比较Fig.3 Comparison of statistical distribution between traditional and improved SoS Method

另外，为了方便观测比较不同方法输出高斯噪声的周期，我们取谐波数目N=16，高斯噪声数目M=4，余弦表深度Dcos=212和宽度Wcos=14，定点化频率位宽Dω=14。从图4(a)、(b)给出了改进前后两种方法输出的周期长度，由图可看出，传统的SoS方法重复周期较短，而改进的SoS方法的重复周期得到了很好地扩展，远远大于传统方法。

图4 传统与改进SoS方法重复周期比较Fig.4 Repeated cycle comparison between traditional and improved SoS method

5 结论

传统高斯噪声产生方法输出统计分布比较精确，但是硬件实现也比较困难。基于SoS的产生方法，原理简单且易于硬件实现，已被广泛应用于无线信道衰落的实时模拟。本文推导了SoS方法输出随机变量幅度的理论分布，并针对其存在输出统计精度差和重复周期短的问题，利用Hadamard矩阵变换思想对其进行改进。数值仿真表明，改进后方法输出的幅值统计分布性能明显优于传统SoS方法，尾巴精确度有所提高，重复周期也大大扩展，比较适合于硬件实时模拟产生高斯噪声。