多基地雷达自适应CFAR检测融合算法

2018-07-25许蕴山夏海宝王嵩乔

信号处理 2018年7期

王楠许蕴山夏海宝王嵩乔

(空军工程大学，陕西西安 710038)

1 引言

在多基地雷达系统中，系统在完成检测时，可以综合利用多部雷达接收信号，获得一定虚警条件下的最高检测概率。在实际应用中，采取信息融合的方式是完成多接收信号处理的常用方法，根据进行信息融合的信息形式的差异，通常将检测融合方法划分为决策级，特征级以及信号级三类。

基于决策级的信息融合是最常用的融合方法，文献[1-2]采取贝叶斯检测方法对各个传感器检测结果进行加权融合，取得了较好的检测性能，但该方法需要已知回波的信噪比信息。通常在多基地雷达中，由于所探测目标的RCS与地面雷达站所处方位有很大的关系，并且具体关系往往无法获知，因此仅仅依据雷达与目标的位置关系，很难估计各部雷达所获得的目标回波信号强度，再加上各雷达站所处环境与自身性能的差异，基本无法获得检测空间单元的目标回波信噪比，从而导致该方法失效。文献[3- 4]研究了检测概率未知情况下的基于决策的检测融合方法，采用蒙特卡洛的方法首先进行参数估计，再利用似然函数进行融合检测，但通常情况下蒙特卡洛方法需要大量重复实验获得，现实中很难效仿。陶然[5]等研究了一种在线自适应检测融合算法，基于Neyman-Pearson准则，通过局部判决估计未知的每个接收站的检测概率，从而实现最优判决融合。文献[6]研究了仅已知虚警概率的情况下进行决策级的信息融合，采取一系列假设进行融合计算，但由于决策级的融合信息量较少，只有在大范围融合中，才可能取到较好的融合结果。针对融合信息量较少的问题，产生了信号级的检测融合方法。文献[7]讨论了关于信号传输过程的衰减等因素进行的检测融合，由于该方法信号传输量过大，实际情况下很难实现。为了缩减信号传输量，胡勤振[8]等考虑了一类双门限的检测融合方法，将超过局部检测门限的信号传送至融合中心进行处理，略去了不必要的信号传输，并证明在确定各个检测单元的信号信噪比情况下，获得了很好检测效果。此外基于Rao检测方法[9-11]，也出现了各类分布式的融合检测方法，但基本上都需要各个检测单元的检测性能参数或者接收信号信噪比等先验信息方可获得较好的融合检测性能。在分布式检测融合框架方面，W.P Tay[12]研究了反馈在分布式检测中的作用。

关于特征级的检测融合方法介绍相对较少。可以证明将各个信号的特征值进行加权融合可以获得最优的贝叶斯检测，其中权值根据信噪比确定。本文摒弃了传统的基于统计算法的权值估计方法，在检验统计量上进行了改变，将检测区域从基于权值形成的超平面划分改变为基于某种约束的超曲面划分，从而完成无信噪比信息的检测融合方法。然后根据该方法，设计了一类无融合中心的基于其他雷达检测信息的自适应门限检测方式。仿真结果表明，该方法具备良好的综合检测性能。

2 CFAR检测融合算法

2.1 虚警似然函数

依据CFAR的门限检测准则，假设检测过程的判决方法为：

(1)

其中门限th满足条件：

(2)

下面引入虚警似然函数，如上所述的检测区域为x1>th，那么其检验统计量x1的虚警似然函数定义为：

（2）量取30 mL花生油倒入炒锅内加热至八成热时加入生姜、蒜米、葱、香菜爆香，然后加入茶叶、花生等其他原料，加10 mL水防黏锅，翻炒至香味渐浓、茶叶脆断即可。

(3)

可以看出，在检测区域，检验统计量所对应的虚警似然函数小于所要求的虚警概率，如果将Pf(x1)作为新的检验统计量，那么该CFAR检测可以等价为：

(4)

下面对基于虚警似然函数的检测融合算法进行推导。

2.2 检测融合算法

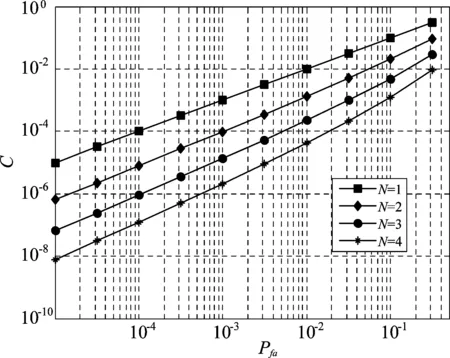
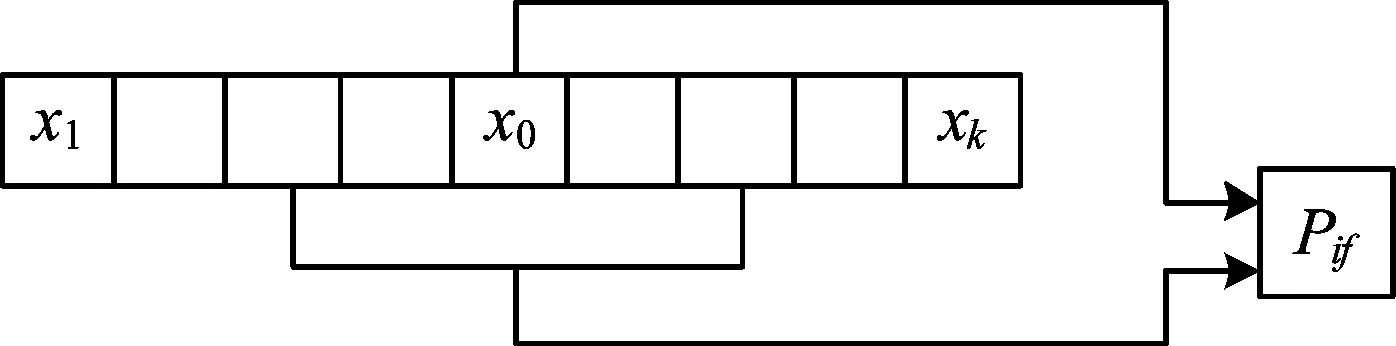
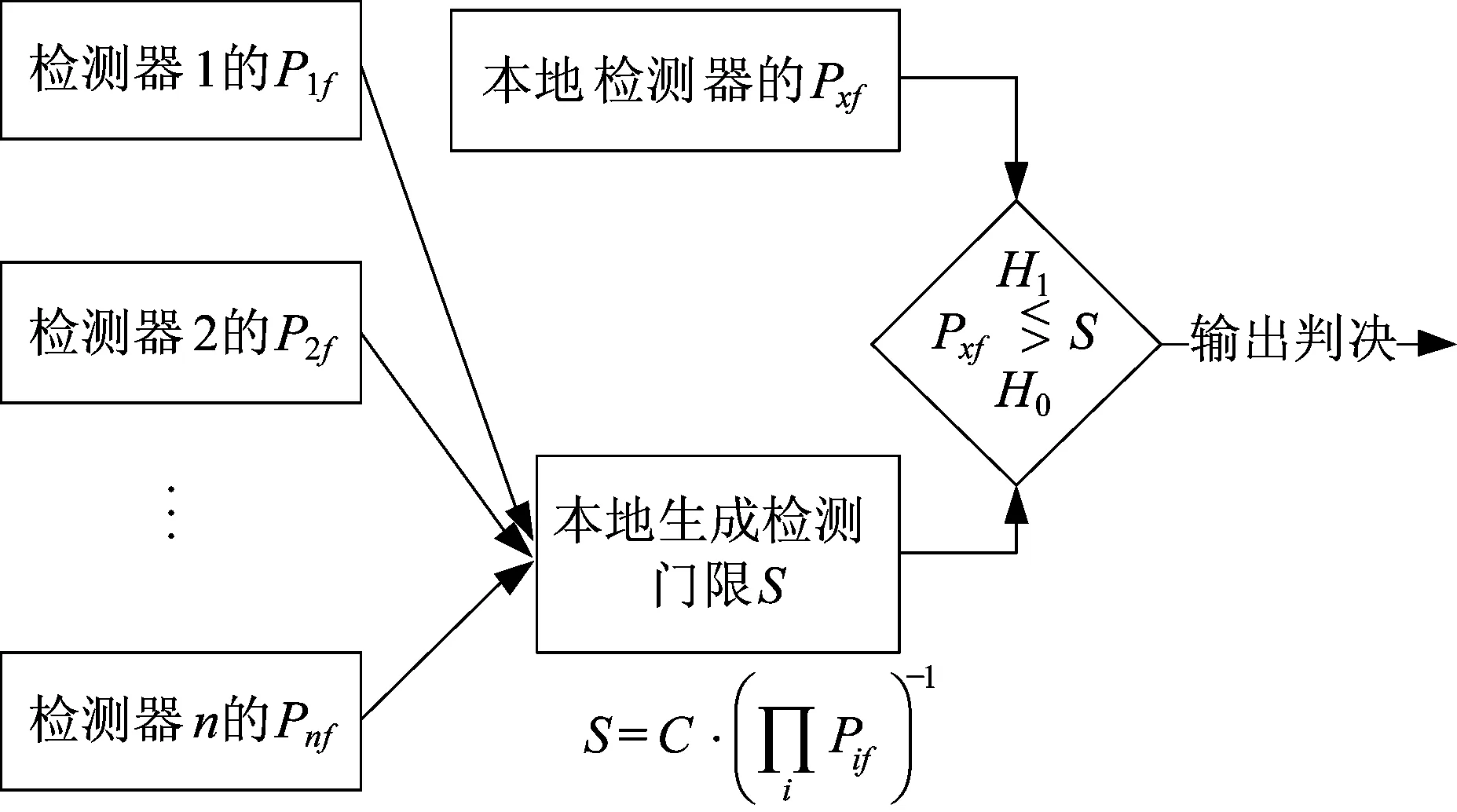
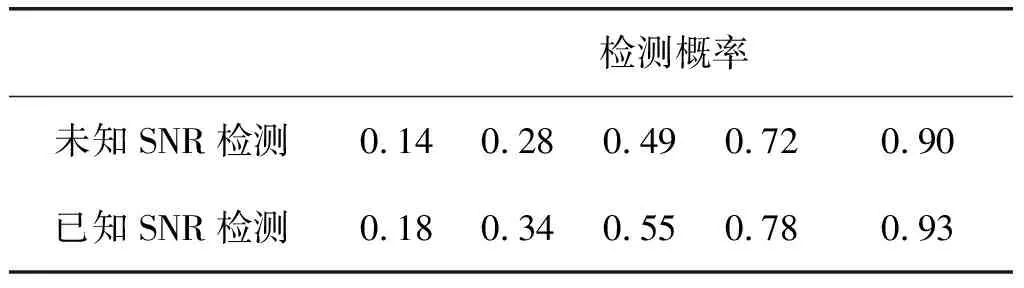
如上所述，在单检测器的门限检测中，当Pf(x1)

图1 一元检测Fig.1 Single detector

考虑两个检测器进行信号检测的问题，各自接收信号的虚警似然函数定义为：

当P1f(x1)P2f(x2)

推导过程如下(换元t1=P1f(x1))：

(5)

根据公式(5)得到Pfa=C(1-lnC)，且0

图2 二元检测Fig.2 Double element detector

此时该方法获得的检测概率Pd为：

(6)

(7)

(8)

这样，当存在N个检测器共同进行检测之时，首先根据所要求的虚警概率，计算出常数C，继而根据各个检测器的虚警似然函数的乘积与C的比较来得到检测结果。

图3给出不同检测器个数，虚警概率变化时，C值的变化情况：

图3 C与Pfa和N关系示意Fig.3 The relation among C and Pfa & N

表1是确定检测器数目N与虚警概率Pfa后得到的C值：

表1 常数C具体数值

3 信号检测模型

3.1 雷达检测单元的检验统计量

根据中心极限定理，在距离单元进行脉冲积累后，检测单元与参考单元的信号幅度都近似服从高斯分布，获得检测单元的虚警似然函数，进行融合检测。

在单部雷达的信号检测中，通常根据杂波水平确定检测门限。实际上雷达根据参考单元获得杂波分布参数，再以一定的虚警概率得到的检测门限，从而确保检测的CFAR性质。根据包络检波原理，单个杂波幅度满足的瑞利分布，其期望方差满足关系：

(9)

图4 积累后计算得到PifFig.4 Calculating Pif after accumulate

根据参考单元可以获得杂波积累后的概率分布参数，从而进行文章第2节所做的检测。根据杂波分布估计参数可以得到雷达检测单元信号的虚警似然函数。

3.2 自适应门限检测架构

考虑利用多雷达组网的优势，设计一种基于其他雷达的已有检测信息，对本地检测器进行动态门限调整的检测方法，假设空间分集通道满足空间和时间配准条件，并且在解决了距离门正确关联的前提下。实现方法如图5所示。

图5 自适应门限检测Fig.5 Adaptive threshold detection

下面是上述检测门限的推导，如前所述，检测判决为H1则有：

其中Pxf为本地检测器的虚警似然函数，而Pif为其他各个检测器的虚警似然函数。该检测架构表明，检测器在接收到其他检测器传递过来的信息后，对自身的门限进行调整，从而在整体上保证了检测的恒虚警性能，与其他检测器之间信息的有效利用。可以证明，该方法可以让系统内任一检测器的检测性能达到融合的检测性能，但代价是必须保证各个检测器之间信息的交互。同样可以将检测器分组进行小范围的融合后再完成大范围的协同，也可以进行分级处理，以消减检测器间通信负担。正是由于虚警似然函数的乘法处理，使得该检测的融合方法灵活且便捷，具体应用还可以参照传统的检测架构。下面是基于该自适应门限检测框架的算法流程。