中段弹道目标微多普勒历程修复算法
2018-07-25许旭光冯存前李靖卿贺思三
许旭光 冯存前,2 李靖卿 贺思三
(1. 空军工程大学防空反导学院,陕西西安 710051;2. 信息感知技术协同创新中心,陕西西安 710077;3. 中国人民解放军93786部队,河北张家口 075000)
1 引言
作为一种可以直接打击敌国战略战役重心的高技术大规模杀伤性武器,弹道目标具有强大的战略威慑力和战役战术打击能力[1]。由于弹道导弹在中段飞行时间较长、弹道易预测等特点,国内外普遍认为中段是弹道导弹防御的重要阶段[2]。微动作为中段弹道目标的一种典型运动特征,对于弹道目标特征的提取与识别具有重要的研究意义。
在弹道目标的观测过程中,由于遮挡效应导致回波采集中断,使得部分时间内微多普勒历程出现缺失现象。文献[3]和文献[4]分别分析了遮挡效应对平底锥形弹道目标以及锥柱形弹道目标的影响,通过仿真和实测数据验证由于遮挡效应导致的微多普勒历程缺失问题,文献[5]研究了遮挡效应对于有尾翼锥形弹道目标尾翼散射中心和滑动散射中心的影响,通过仿真验证遮挡效应对各散射中心一维距离像历程的影响。但是上述文献并没有针对这一问题提出相应的解决办法。如果直接使用缺失的微多普勒历程对弹道目标相关特性进行分析,会增加弹道目标微动特征提取的难度,影响弹道目标识别的有效性。
作为一种新型采样理论,压缩感知能够打破传统采样理论的限制,以少量的观测信号实现对原始信号的重构,因而广泛的应用于信号处理、图像处理、医学成像、光学成像、电磁学等领域[6]。当前,基于压缩感知的数据修复研究已经取得一定成果。文献[8]基于压缩感知理论实现对振动数据的恢复,并且通过计算机仿真和实测数据验证算法有效性;文献[9]采用基于贝叶斯压缩感知的图像修复方法对受损图像进行修复。
本文以平底锥形弹道目标作为研究对象,在弹道目标滑动散射中心进动模型的基础上,分析不同视角下遮挡效应对散射中心微多普勒历程的影响;针对遮挡效应导致的微多普勒历程缺失问题,设计压缩感知框架下的观测矩阵,通过贪婪算法中的SP算法实现微多普勒历程高精度修复;通过将本文提出算法与傅里叶插值和多项式拟合修复算法的比较分析,说明文中所提算法的有效性;通过分析不同数据缺失率下本文算法的重构效果,分析该算法的使用条件;最后对全文内容进行总结。
2 弹道目标滑动散射中心进动模型
文献[10]结合仿真数据和暗室测量数据证明:滑动散射中心模型比理想散射中心模型更符合弹道目标实际运动情况。基于此,建立弹道目标滑动散射中心进动模型如图1。
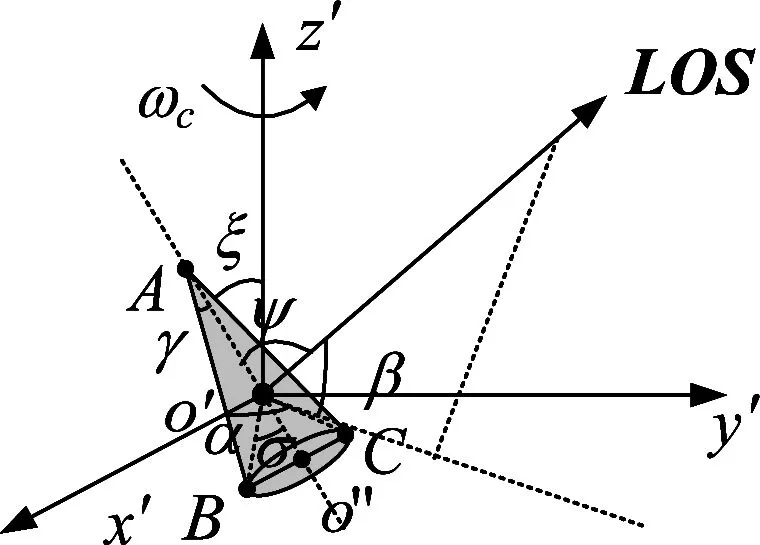
图1 滑动散射中心进动模型Fig.1 The model of procession target of sliding scatter
雷达视线的单位方向向量:
η=[cosαcosβ,sinαcosβ,sinβ]T
(1)

e=[sinξ,0,cosξ]T
(2)
t时刻弹体对称轴的单位方向向量表示为:
ed=[sinξcos(ωct),sinξsin(ωct),cosξ]T
(3)
联立式(2)和式(3),则有雷达视线与对称轴夹角的余弦值cos(ψ)为
cos(ψ)=sinξcosβsin(ωct+α)+cosξsinβ
(4)
根据散射中心在弹头中的几何分布,可以得出各散射中心的微距离表达式为:
(5)
式中:R0为雷达到参考坐标系原点o′的距离。
微距离R和微多普勒fd之间的关系为:
(6)
式中:λ为雷达发射电磁波波长。根据式(6)可得各散射中心的微多普勒表达为:
(7)
由式(7)中知:锥顶A的微多普勒历程呈标准的正弦函数,B和C两个滑动散射中心微多普勒历程受到观测视角、弹体物理结构特征、锥旋角频率等参数调制,表现为非标准的正弦形式。
3 弹道目标遮挡效应分析
为分析遮挡效应对弹头各散射中心的影响,建立圆锥弹头等效散射中心模型如图2所示。
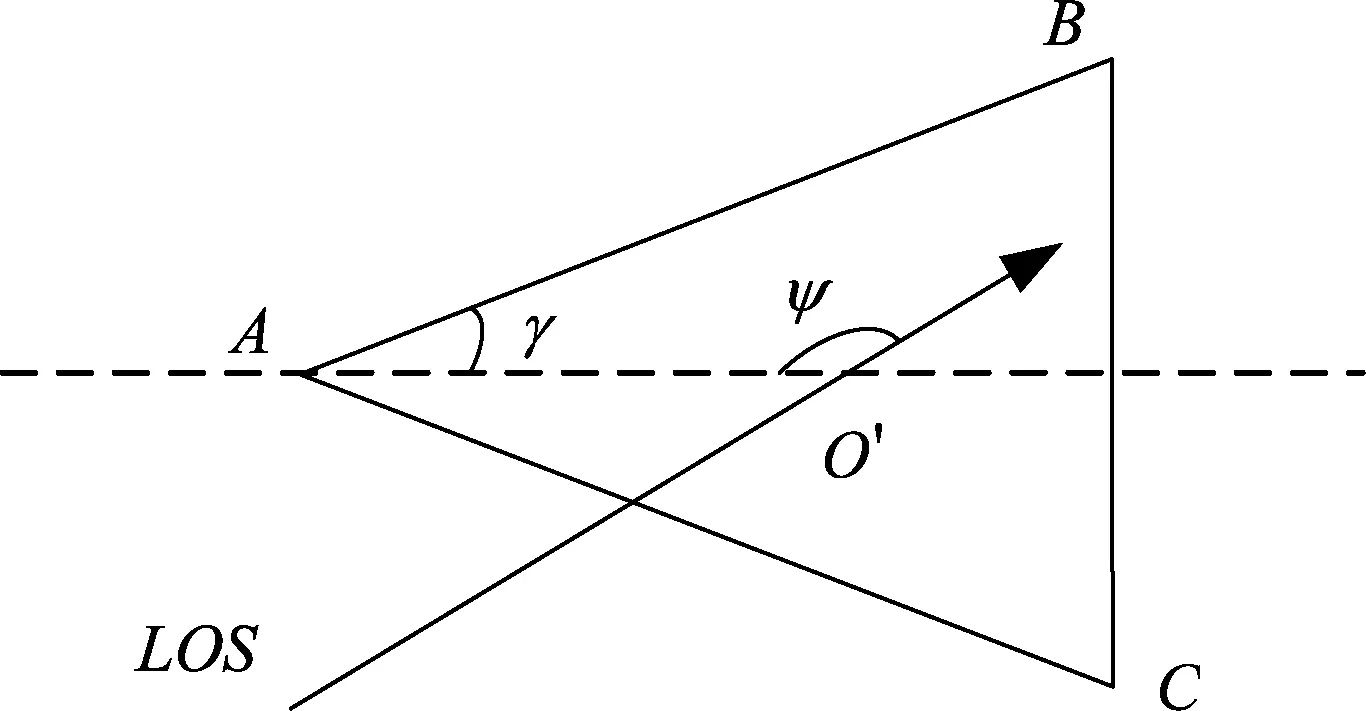
图2 等效散射中心示意图Fig.2 The sketch map of equivalent scatter
通过几何分析可以得出,当雷达视线LOS与弹体对称轴夹角ψ和弹道目标半锥角γ满足某些数学关系时,弹道目标等效散射中心处于被遮挡的状态。具体分析如表1所示。
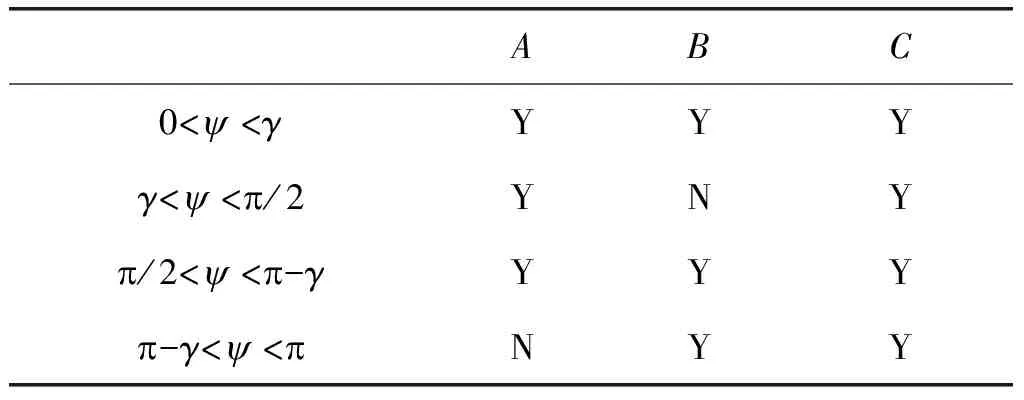
表1 散射中心可见性与雷达视角关系
表1中,“Y”表示散射中心未被遮挡,能够有效散射回波;“N”表示散射中心被遮挡,无法有效散射回波。
综上,当考虑遮挡效应对弹道目标微多普勒历程的影响时,微多普勒历程可以修正为:
fd=fd×u(t)
(8)
式中:

(9)
考虑到弹道目标在空间微动状态具有周期性,u(t)应当为一个周期函数,其具体表达形式由观测视角和半锥角的数学关系决定。
4 微多普勒历程修复原理
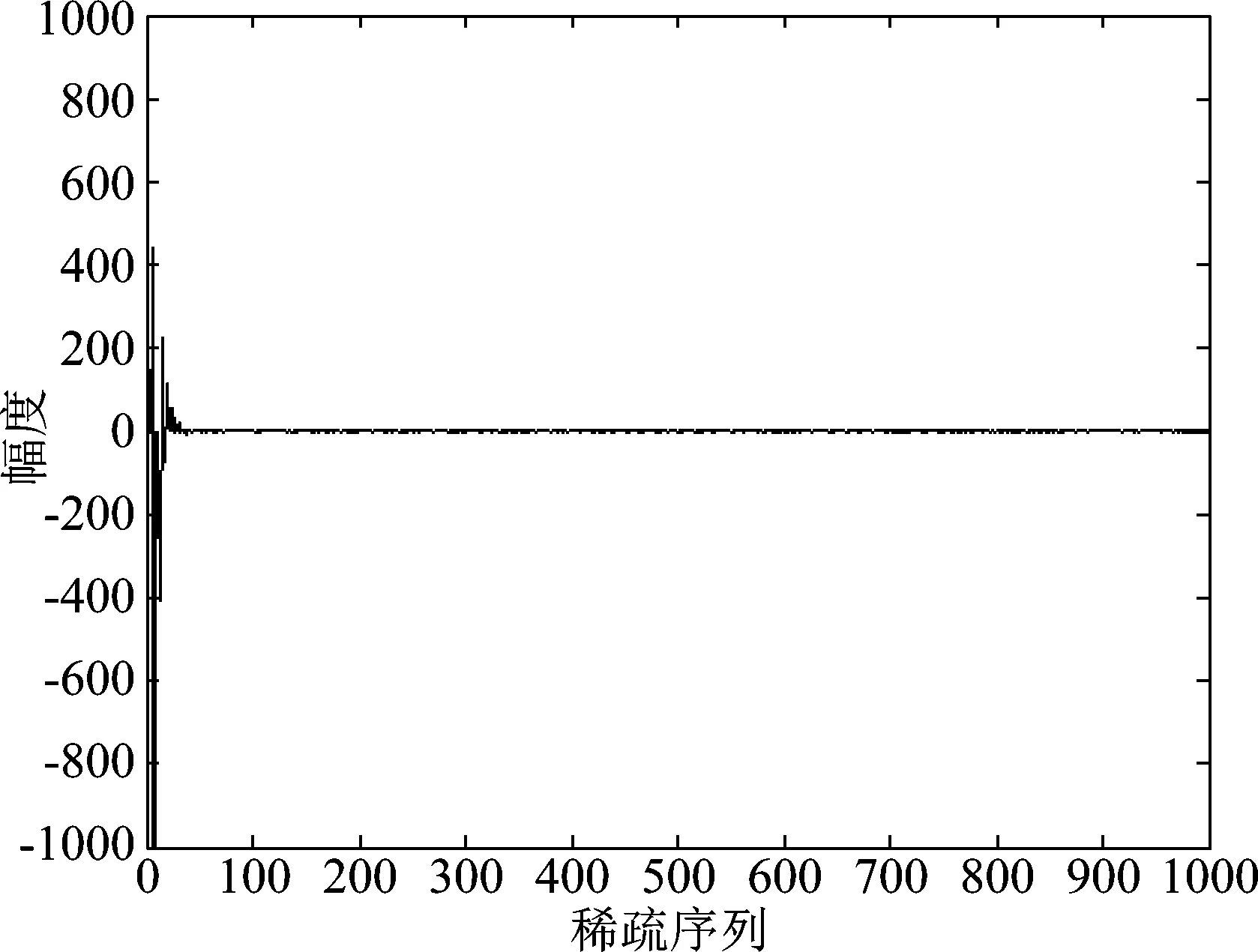
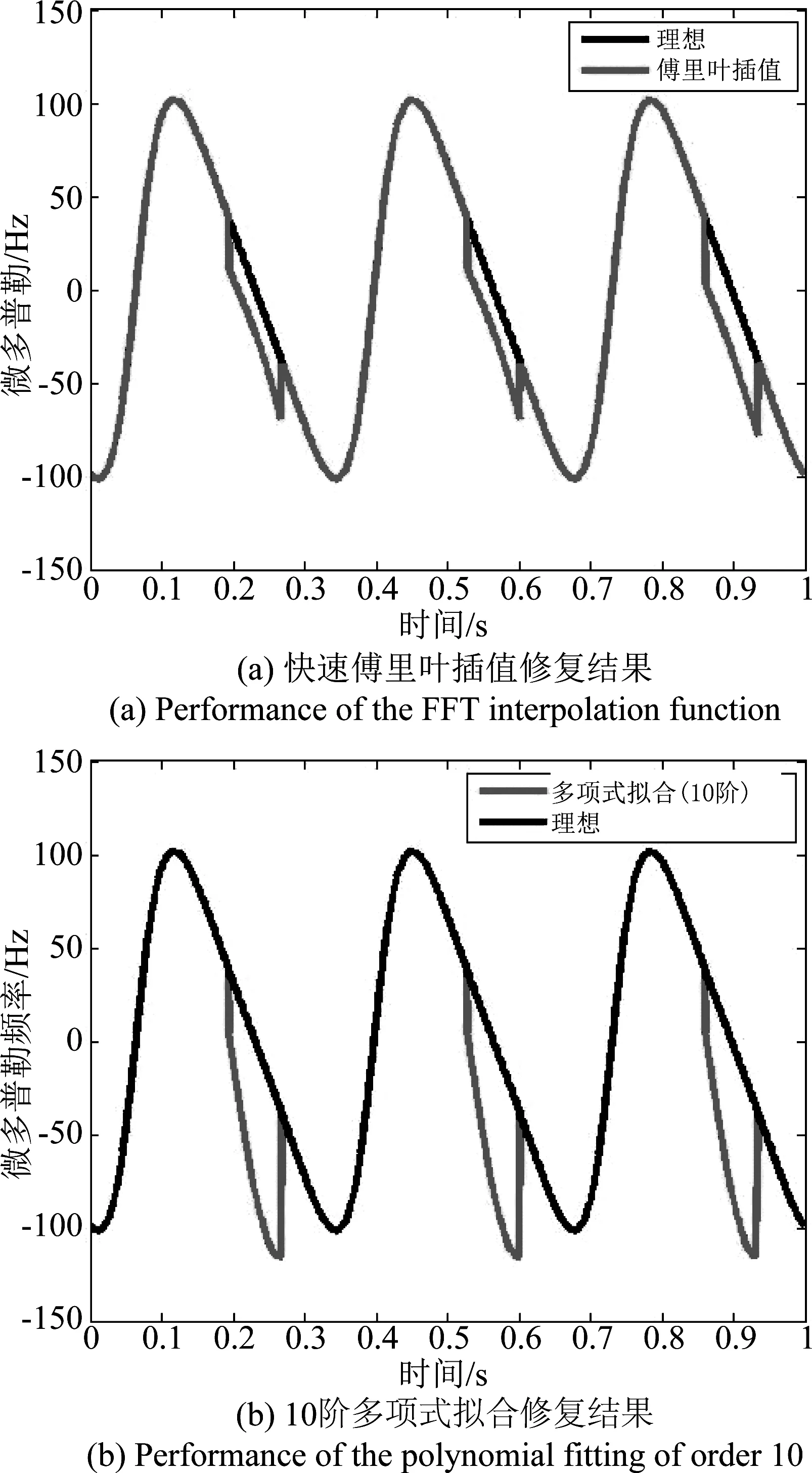
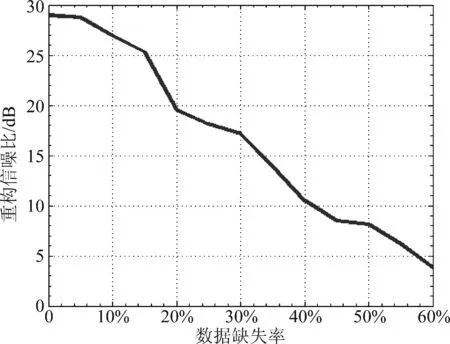
根据压缩感知原理,若信号xN×1本身或在某个变换域是稀疏的,即稀疏系数中只有少量非0元素,则对信号进行随机压缩采样得到yM×1(M (10) Step 1 取单位矩阵IN×N; 若x在稀疏基矩阵Φ下可以表示为 x=Φθ (11) 式中:θ为稀疏系数。 则上述重构问题可以表示为 (12) CS理论发展至今已经产生多种重构算法,主要由包括凸松弛算法、贪婪算法、迭代阈值算法等[13]。贪婪算法由于运转速率低、重构精度高而得到广泛应用[14]。常见的贪婪算法包括匹配追踪(MP)、正交匹配追踪(OMP)、压缩采样匹配追踪(CoSaMP)等。本文采用SP(Subspace Pursuits)对缺失的微多普勒历程进行重构。 算法流程如下: Input:压缩感知矩阵T,观测数据y,稀疏度K。 Step 1 令初始残差r0=y,迭代次数t=1,索引集合Λt=∅,At由Λt对应压缩感知矩阵T中的列向量组成,设At=∅。 Step 2 计算u=| 与OMP、MP等重构算法相比,SP每次在感知矩阵中选取多个原子,可以有效减少迭代次数,提高运算效率。 假设雷达发射单载脉冲信号,载频为f0=10 GHz,脉冲重复频率为fr=1024 Hz,积累时间为T=1 s目标为圆锥弹头,h1=1 m,h2=0.6 m,底面半径r=0.8 m,半锥角γ=26.6°,雷达视线的方位角和高低角(α,β)=(20°,70°);弹头锥旋角ξ=8°,频率ωc=8π rad/s。不同散射中心的散射系数不同,本题假设A、B、C散射中心散射系数之比为1.5∶1∶1。 图3(a)为不考虑遮挡条件下三个散射中心的微多普勒历程。通过图3(a)分析得到:A点的微多普勒历程为标准的正弦形式,而B点和C点的微多普勒历程呈现出非标准的正弦形式,这与第2节中分析是一致的。当考虑遮挡效应对回波的影响时,可以看出图3(b)中散射中心B的微多普勒历程在部分时间内间断,在仿真图中表现为某些时间范围内微多普勒频率为0,从而验证了遮挡效应对微多普勒历程的影响。 图3 各散射中心微多普勒历程 Fig.3 Each scatter’s micro-Doppler histiory 为了对B散射中心缺失的微多普勒历程进行重构,首先对理想条件下微多普勒历程在离散余弦基下进行展开,得到其稀疏系数序列如图4。图4中可以看出,只有少部分稀疏系数时非0的,绝大部分稀疏系数均为0,这说明微多普勒历程在离散余弦基下是稀疏的,为后续实现基于SP算法条件下的微多普勒历程实现有效恢复提供先决条件。 图4 散射中心B理想微多普勒历程在离散余弦基矩阵下稀疏系数Fig.4 Sparse coefficient of ideal micro-Doppler history of scatter “B”in DCT matrix 采用SP算法对缺失的微多普勒历程进行重构,效果如图5中绿色曲线所示。分析可以发现,重构后的微多普勒历程与理想微多普勒历程基本重合,即本文算法实现了微多普勒历程的高精度重构。 图5 基于SP算法的微多普勒历程修复结果Fig.5 Performance of SP algorithm to recover the micro-Doppler history 常见的缺失信号修复算法包括插值法、曲线拟合法、谱估计法以及时变自回归算法等[15]。分别采用快速傅里叶插值法和多项式拟合法对微多普勒历程进行修复,效果如图6所示。 图6 不同方法修复微多普勒历程Fig.6 Different ways to recover the micro-Doppler history 从图6中可以看出,基于傅里叶插值和基于多项式拟合的微多普勒历程修复方法对于微多普勒历程修复效果相对较差,与理想微多普勒历程的差异性比较明显,与本文算法的重构精度相比还存在较大差距。 文献[16]中指出:基于压缩感知的数据重构算法的重构效果与观测数据的数量有较大关系。因此,本文拟分析在不同数据缺失率下的数据文中所提算法的修复效果。引入重构信噪比(PSNR)来分析该算法的重构效果: (13) 式中,x为原始信号,x″为重构后的信号。 由图7可以看出,随着数据缺失率的增高,文中所提的方法的重构效果越来越差。在仿真实验中可以看出,当数据缺失率达到50%以上时,重构信噪比在8 dB左右,仿真发现此时已无法有效修复出完整的微多普勒历程。因此,本文提出的算法是有适用条件的,当数据缺失低于50%时,本文提出的算法可以得到较好的重构效果;当缺失率较大时,数据结构被严重破坏,此时则无法实现微多普勒历程的有效修复。 图7 数据缺失率对重构效果的影响Fig.7 The effects on reconstruction performance of the data missing rate 本文通过对锥形弹头滑动散射中心建模,验证滑动散射中心与理想散射中心微多普勒历程之间的差异。对由于遮挡效应导致的散射中心微多普勒历程缺失的问题,提出一种基于CS理论的缺失数据补偿方法,通过与基于傅里叶插值和多项式拟合的数据修复算法的修复结果相比较,验证本文算法的有效性,同时进一步分析数据缺失率与算法重构效果之间的关系,指出本文算法的使用条件。通过本文提出算法,可以实现微多普勒历程的重构,为不完全观测条件下的微多普勒历程修复提供参考方法,为后续基于完整微多普勒历程的弹道目标特征提取和参数估计打下良好的基础。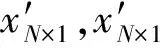




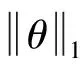
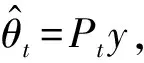
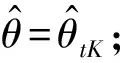
5 仿真分析



6 结论
