联合波形重构的数字调制信号直接定位方法
2018-07-25余婉婷于宏毅杜剑平
余婉婷 于宏毅 杜剑平 王 鼎
(信息工程大学信息系统工程学院,河南郑州 450001)
1 引言
目标的精准定位,在许多领域都有着重要作用。无源定位技术的发展进步与雷达等有源设备和无线电通信技术的发展密切相关。当前无源定位通常采用传统两步定位算法,首先由各接收站对目标信号定位观测量进行测量。这些观测量包括到达角度[1-2](Angle of Arrive, AOA),到达频率(Frequency of Arrive, FOA),到达频率差[3- 4](Frequency Difference of Arrive, FDOA),到达时间(Time of Arrive, TOA),到达时间差[5- 6](Time Difference of Arrive, TDOA)和接收信号能量[7- 8](Received Signal Strength, RSS)等。然后由中心站汇总这些观测量进而构建目标的位置和状态,通过一些优化算法进行定位解算估计目标辐射源的位置参数。从信息论的角度看,传统两步定位法忽略了各信号同源这一关键信息,需要通过数据关联的方式完成观测参数与目标位置之间的匹配,目标数增多的时候存在组合爆炸问题;其次传统两步法多站通过观测参数进行定位的方法缺乏底层信号数据的融合,分步处理环节产生信息损失,使得算法定位精度受限。电磁环境日益复杂,传统方法在低信噪比以及许多复杂条件下的定位精度还有提升空间。
针对传统两步定位法的局限,一种由中心站直接获取目标位置无需估计中间参量的单步定位体制,直接定位(Direct Position Determination, DPD)体制被提出。DPD的本质在于融合数据重构定位场景,根据最大似然(Maximum Likelihood, ML)准则或者多重信号分类原理,直接给出使代价函数最小的联合位置估计结果。算法无需分步计算目标辐射源的位置参数,一方面充分利用目标信号同源的条件,对各站底层接收数据直接进行数据融合处理,另一方面对参数矩阵进行联合估计,有效解决了传统两步法中参数与目标位置之间失配等问题[9]。DPD算法以其低信噪比和复杂环境下的更高的定位精度和更强的鲁棒性,受到越来越多学者的关注。一些改进算法如基于位置信息场的DPD方法[10],基于期望最大化(Expectation-maximization, EM)的DPD算法[11],基于子空间分解压缩感知的DPD算法[12],针对特定信号的(OFDM信号[13]、循环平稳信号[14]以及恒模信号[15-16]等)的DPD算法,联合时延和多普勒频率等参数的DPD改进算法[17-20]等,也在特定场景下表现出了良好的性能优势。由于它要将大量观测数据直接传输给计算节点运算,该类算法计算量较大,需要占用较宽的传输频带。但是随着信号传输带宽增大和计算机数据处理能力大幅提高,对目标位置直接估计的方式(即单步定位体制)在未来实际工程中的应用场景十分广阔。
信号特征、设备对信号的接收能力以及现代计算机对数据处理能力,是决定定位方法选取的重要因素。研究表明信号波形已知的直接定位算法能够达到更高的定位精度[21],但实际无源定位场景中信号波形往往难以先验已知,未知信号波形的直接定位算法精度受限,这在一定程度上限制了直接定位算法在无源定位系统中的应用。文章针对无源定位中普遍存在的调制方式已知,符号信息未知的数字调制信号,提出一种基于多站联合波形重构的数字调制信号直接定位(Direct Position Determination for digital Modulation signals, MDPD)方法,旨在为直接定位算法在无源定位系统中的应用提供一定的算法和实验基础。通信系统中对信号的解调与定位参数的测量通常由各接收基站分离处理,这种分步处理体制忽略了辐射源位置信息对解调符号估计的约束。实际上,解调与位置估计是耦合的,分离成两个环节分别处理理论上无法得到最优估计,特别是信噪比较低时,接收站解调误码率增加,得到的不准确信号波形信息将严重影响直接定位精度。综上所述,研究准确有效的信号参数估计方法,对DPD定位方法的性能提升有着重要意义。若能够获取并运用更准确的波形先验信息,理论上可以进一步提高直接定位算法性能。文中首先建立了多站联合直接定位算法的接收信号模型,然后在波形未知的直接定位结果基础上,结合调制信号符号成型规律给出了信号波形的最小二乘估计和符号序列检测结果,最后将符号序列重构信号波形用于获取目标位置的最大似然估计。仿真实验表明本文提出的方法定位精度优于传统两步定位法和针对未知信号直接定位方法,性能更接近相应的直接定位CRLB。
2 信号模型和问题分析
星座图是数字调制信号的重要特性之一,星座聚类点的位置关系体现了信号的调制特征,并且任何一种数字幅相调制信号都可以用复平面上唯一的星座图表示。已知调制方式时,源信号复基带时域信号模型可以表示如下:
(1)
其中复数α(xk)为信号星座图复平面中的不同聚类点,对应信号中承载的符号xk,记为αk。取值由源信号的调制方式确定;符号序列长度为K,各个符号独立同分布且满足|αk|2=1;g(t)为参数已知的升余弦滤波器;T为符号周期。
考虑多站单目标定位,假设目标处于静止状态,坐标为p,L个安装有M元直线阵列的接收站位置固定且坐标已知。直接定位算法的精度不仅会受到有限采样的影响,一些可能的模型误差或者阵列误差也会破坏阵列接收场景下的数学模型,其中信道的不稳定性、多径效应等,也会影响算法定位精度。为了重点研究基于信号波形特征的直接定位算法,因此模型假设定位场景为视距场景,仿真条件假设信道衰落为常数。多站联合直接定位方法的示意图如图1所示,目标源信号被各基站天线阵列接收后,直接通过数据传输到中心站进行联合处理。

图1 多站联合直接定位方法示意图Fig.1 Multi-station joint direct positioning method diagram
假设源信号为窄带信号且接收站时间同步,则第l个接收站输出的接收信号复包络可表示为:
rl(t)=blal(p)s(t-tl)+nl(t),
l∈[1,L];t∈[1,Tm]
(2)
其中,bl为体现目标到各个基站间信道衰减的未知复标量,模型假设信号到各接收站视距传输;al(p)为基站l对于目标辐射源信号的阵列响应,当定位距离远大于阵列孔径时,这里的阵列响应仅与信号到达方位角有关;s(t-tl)为第l个接收站接收信号的复包络,其中tl=τl(p)+t0;τl(p)表示源信号传输到各个基站的传输延迟,与目标位置有关;由于基站间时钟频率同步,不考虑载波残余频偏,信号源相对各基站的发射初始时间t0已知值;nl(t)表示第l个接收站的阵元噪声向量,设为实部虚部相互独立的零均值加性复高斯白噪声,噪声功率为σ2。
将接收信号进行每符号Z倍采样做傅里叶变换到频域,可以分离信号中的时延项。取等间隔的频点数J,定义:
(3)
则各接收阵列的频域观测向量可以联合表示为如下矩阵形式:

(4)
其中:
A(j)=Γ(p)Hβ
β=[b1,…,bL]T
H=IL×L⊗1M×1
α=[α1,α2,…,αk]T
x=[x1,x2,…,xk]T
(5)
式中⊗表示Kronecker乘积;IL×L表示大小为L×L的单位矩阵,1M×1表示元素全为1的M列向量。此时与目标位置有关的信息全部包含在了A(j)中。
假设噪声功率σ2已知,可以得到如下非线性最小二乘优化模型:
(6)
假设目标到各个基站间信道衰减系数β与其目标位置坐标p独立,可以将两者解耦合处理[22],推导得到β关于p和α两个参数的最优闭式解后带入目标函数,则优化模型转化为了对目标函数Q(β,p,α)中p和α两个未知参数的估计问题。
3 调制方式已知的直接定位方法
3.1 基于多站联合波形重构的直接定位方法原理
利用最大似然的思想,通过目标区域内代价函数的极值搜索,得到符号估计序列对应的目标辐射源位置坐标最优解。采用联合估计的方法求解第二节目标函数Q(β,p,α)中p和α两个未知参数,搜索维度为K+D,其中D为坐标维度,取值2或3。当符号长度K较大,搜索维度增大,算法复杂度会大幅升高[23-24]。针对符号较长的序列,本文提出基于波形重构的MDPD方法,用n次D维搜索交替迭代代替了K+D高维搜索。本文定位方法原理图如图2所示,下面具体描述了方法步骤:
1)波形未知的目标位置估计。各站接收阵列截获的目标信号通过数据传输通道传给中心站进行处理,中心站首先根据波形未知的直接定位方法,估计目标位置,得到迭代初值。波形未知的DPD算法适用范围广,计算复杂度低,仅通过低维搜索就能迅速获取目标位置。由于未考虑源信号本身携带的特征信息,位置估计的精度还有待进一步提升。
2)调制方式已知的符号序列估计和波形重构。建立关于接收数据样本频域的最大似然函数,得到波形估计的最小二乘模型。利用上一步得到的目标位置初值,在已知信号的调制方式的条件下,通过符号检测和波形生成,重构目标信号波形。
3)基于重构波形的直接定位算法。利用重构波形,建立联合调制信号波形的直接定位算法模型,估计定位结果。
4)目标位置更新与迭代。判断是否达到终止条件(连续几次迭代目标位置精度提升效果不明显),未终止则将定位结果代回波形估计过程,得到更加精确的符号估计序列,重复步骤3)更新定位结果。

图2 基于重构波形的直接定位算法原理图Fig.2 DPD algorithm based on reconstructed waveform
3.2 波形未知的DPD算法
各个接收阵列的频域观测向量可以联合表示为如下矩阵形式:
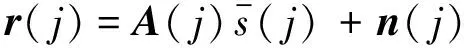
(7)
(8)
其中矩阵D是关于各站坐标,接收数据,阵列响应,以及未知目标位置的函数。矩阵形式为:
(9)
式中Us(j)为包含信号波形自相关矩阵的最大特征向量。通过低维搜索即可得到矩阵D(p)的最大特征值,给出未知信号的直接定位结果:
(10)

3.3 调制方式已知的符号序列估计与波形重构
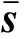
(11)
式中:
Al(j)=blal(p)e-iωjτl(p)
(12)
考虑每个接收阵列的阵元数量时,矩阵al(p)可以拆分为alm(p),是一个维度为J×1的阵列响应列向量,满足al(p)=[al1(p),…,alM(p)]T。对应ALM为M×L×J行,J列的联合阵列响应矩阵,为了得到波形的最小二乘估计结果,将式(11)中的阵列响应矩阵写成块状矩阵的形式:
(13)
(14)
结合阵列接收信号的矩阵形式:
(15)
进一步得到A(j)的伪逆A+(j)表达式:
A+(j)=[AH(j)A(j)]-1AH(j)
(16)

(17)

在符号序列检测问题中,需要通过定时参数恢复最佳抽样点,可以证明最佳抽样点是符号估计的充分统计量[25],表达式为:
(18)
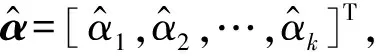
(19)
3.4 基于重构波形的MDPD算法

(20)
假设信号与噪声不相关,噪声已知为空间白噪声,定义矩阵:
(21)
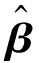
(22)
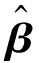
(23)
式(23)的结果容易通过Newton迭代优化求解得到,具有较快的收敛速度且无需高维搜索。式中:
(24)
3.5 方法总结与讨论
根据上述讨论,给出基于多站联合波形重构的调制信号直接定位方法的计算步骤如下:
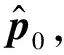



关于上述方法步骤有如下几点说明:
注释1 步骤1中波形重构的DPD算法在本文方法中的作用相当于给定迭代初值,这个初值选取相比其他方法,速度快,精度要高,合适的初值也有效地减小了重复计算的次数。仿真实验表明,步骤1中给出的初值能够保证计算方法最终得到较好的估计值。
注释2 从信息论的角度分析容易得到,{ε(m)}m∈[0,)是个有界的并且总体呈递减趋势的序列,因此设定合适的迭代终止门限e,上述迭代方法在重复计算过程中能够进一步提高定位估计精度,但需要多少次迭代重复计算或者能否达到全局最优解尚无严格的数学证明。每次迭代包括一次波形重构和位置解算,算法中波形重构相对于位置解算复杂度低,因此本方法的计算复杂度主要来自于每次定位解算的D维搜索,其中D取值为2或3。仿真实验表明仅需有限次的迭代就能达到较为理想的性能提升效果。
注释3 为了对本文方法的定位性能进行研究,需要将方法与直接定位算法理论性能进行对比。在只考虑加性噪声,不考虑定位模型误差的条件下,本文方法的CRLB参考信号波形已知的直接定位算法,波形已知条件下直接定位算法无偏估计均方根误差的克拉美罗界为[22]:
(25)
其中,
(26)
仿真实验也表明,随着信噪比增加,算法估计值能够较好地收敛到注释3所给出的CRLB。
以上是本文方法的算法原理和数学模型, 3.2给出了直接定位场景下的未知信号波形的定位结果,为MDPD方法提供了位置估计初值;3.3中重点讨论了中心站收到信号数据后,对目标信号的符号序列估计以及波形重构结果;3.4基于前一节中的重构波形,建立了调制信号波形已知的MDPD算法模型。后文将从重构信号误码率和不同方法定位误差对比两个方面,通过仿真实验对本文方法性能进行研究。
4 仿真实验
为了研究波形重构过程对定位性能的影响,验证方法性能,本文从符号估计误码率和定位误差对比两个方面,进行了蒙特卡洛仿真实验。实验中每个基站装备阵元数M=9朝向目标位置的直线阵天线,目标发射源位置坐标(0, 0),目标到各个基站的信道衰减均为1。布站方式不同时,目标区域内的定位精度也发生改变,表1选取了两类典型布站方式,图3首先给出了信噪比为-10 dB时布站方式改变时目标区域内的定位误差GDOP分布。

图3 布站方式改变时目标区域内GDOP分布图Fig.3 Distribution of GDOP in the target area with different station mode
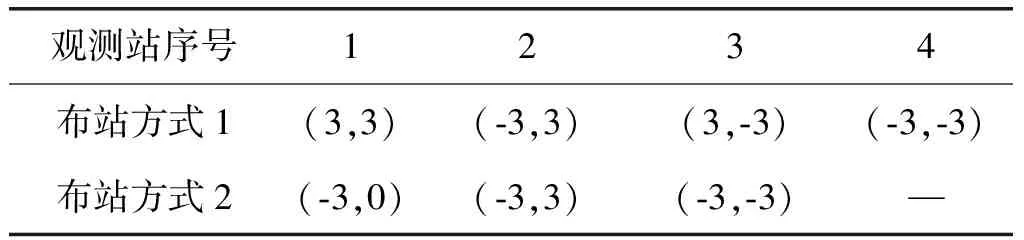
观测站序号1234布站方式1(3,3)(-3,3)(3,-3)(-3,-3)布站方式2(-3,0)(-3,3)(-3,-3)—
对比图3(a)和图3(b),四个接收基站四周布站的定位精度比三个接收基站线性布站的定位精度高,这表明定位精度与基站布站方式、目标与基站的相对位置都有关,这也是实际定位基站选取的重要参考因素之一。但布站结构不影响相同场景下几种定位方法的精度对比。因此,为了便于与现有算法进行性能对比,本文布站场景参照Weiss团队相关文章中,直接定位与两步法定位对比时选取的四个观测站均匀布站方式。仿真场景位置示意图如图4所示,四个接收基站,位置坐标分别为(3000,-3000),(3000, 3000),(-3000, 3000),(-3000,-3000),单位m。

图4 定位场景坐标分布示意图Fig.4 The position coordinates of the four base stations and the target
4.1 重构波形的误码率分析
各接收站将接收信号传输到中心站进行处理,利用未知信号波形的直接定位算法模型得到目标位置初步估计结果,带入波形估计的最小二乘模型进而得到调制信号的符号估计序列。符号估计序列决定了波形重构的准确性,进而影响了后续基于重构波形的定位估计。因此,符号估计误差能够在一定程度上表现方法性能。本节选取MPSK和MQAM两类典型的数字调制信号符号估计误码率随信噪比变化情况,来体现波形重构的准确程度。为了保证误码率计算结果的可靠性,需要足够长的符号序列和多次实验,实验中源信号符号序列长度取217,本文仿真实验基于信号带内信噪比,取带内信噪比从-20 dB到5 dB变化。符号速率10 kHz,每符号4倍采样,采样速率40 kHz,载波频率50 kHz。图5和图6分别是QPSK和16QAM两类信号分别在10 dB和-10 dB两个信噪比条件下重构波形对应的信号星座图分布情况,图像表明,方法中的最小二乘波形重构模型在高信噪比时能够较为准确地估计原始星座点分布情况。两幅星座图是通过符号估计得到的重构波形对应的星座图,与传统解调不同,本文波形重构过程引入了目标位置信息,且利用多站信号数据融合。这部分仿真结果旨在说明联合多站信号并引入目标位置信息,在信噪比较低时,能够实现源信号的波形重构。同时本节仿真数据为节4.2实验分析MDPD方法的定位性能提供了实验参考。
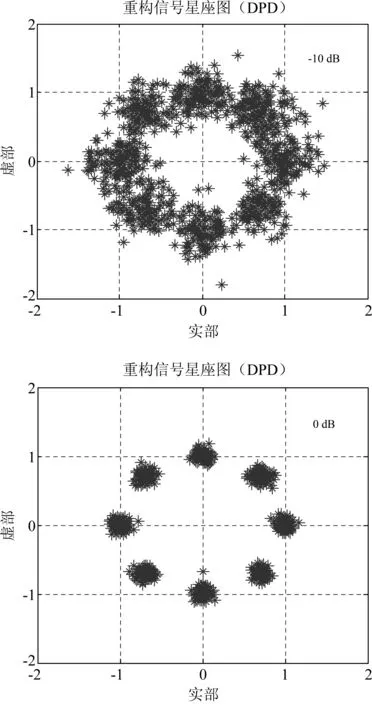

图5 信噪比为-10 dB、0 dB和10 dB条件下的8PSK信号重构星座图Fig.5 The constellation diagram of 8PSK reconstruction signal (SNR=-10 dB, 0 dB and 10 dB)


图6 信噪比为-10 dB、0 dB和10 dB条件下的4QAM信号重构星座图Fig.6 The constellation diagram of 4QAM reconstruction signal (SNR=-10 dB, 0 dB and 10 dB)
进一步研究重构波形误码率,在信号平均功率相同的条件下,对PSK和QAM两类信号经波形重构后的误码率进行研究,结果如图7、图8所示。图7为BPSK、QPSK、8PSK和16PSK四类调制方式的目标源信号误码率随信噪比变化曲线,从图中可以看出,信噪比-20 dB到5 dB范围内,BPSK信号波形重构误码率始终低于0.1,其他三类调制方式信号误码率低于0.1的信噪比门限分别为-17 dB、-12 dB和-6 dB。图8为4QAM、8QAM、16QAM和32QAM四类目标源信号误码率随信噪比变化曲线,四种调制方式信号误码率低于0.1的信噪比门限分别为-18 dB、-12 dB、-9 dB和-6 dB。实验结果显示,当信噪比高于-5 dB时,四类调制信号误码率均低于0.1,说明联合多站信号并引入目标位置初步估计的波形重构结果,在信噪比误码率较低时,就能够降到低误码率水平。

图7 BPSK、QPSK、8PSK和16PSK四类调制方式的目标源信号误码率随信噪比变化曲线Fig.7 The SER for BPSK, QPSK, 8PSK and 16PSK signals versus SNR

图8 4QAM、8QAM、16QAM和32QAM四类目标源信号误码率随信噪比变化曲线Fig.8 The SER for 4QAM, 8QAM, 16QAM and 32QAM signals versus SNR
4.2 定位算法误差分析
参考4.1中的仿真数据,本节实验进一步研究了基于波形重构的直接定位方法性能。选取了四种方法进行对比:1)传统两步定位方法(MUSIC算法+Taylor级数迭代算法);2)未知源信号波形的直接定位算法;3)信号波形完全已知的直接定位算法;4)本文基于多站联合波形重构的直接定位方法。
利用蒙特卡洛实验得到的目标整体定位均方根误差(RMSE)来衡量算法性能,其度量方式如下:
(27)

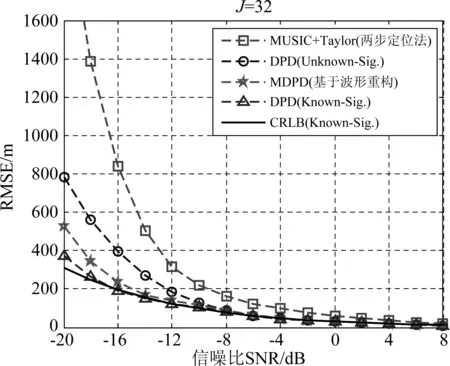
图9 四种定位算法定位均方根误差(RMSE)随信噪比变化的对比图(J=32)Fig.9 RMSE of MDPD on three different methods and the CRLB for known signals versus SNR (J=32)

图10 四种定位算法定位均方根误差(RMSE)随信噪比变化的对比图(J=64)Fig.10 RMSE of MDPD on three different methods and the CRLB for known signals versus SNR (J=64)

图11 四种定位算法定位均方根误差(RMSE)随信噪比变化的对比图(J=128)Fig.11 RMSE of MDPD on three different methods and the CRLB for known signals versus SNR (J=128)

图12 三种频点数下直接定位算法RMSE对比分析图Fig.12 RMSE of MDPD in three different frequency points and the CRLB theoretical curve
从图9~图12中可以看出:
(1)文中提出的基于波形重构的MDPD方法的定位精度要优于已有的未利用信号波形特征的DPD算法,性能接近理论最优定位精度,特别是在低信噪比条件下,方法性能优势明显。这是因为本文方法联合了调制信号的符号估计与波形重构,充分利用了数字调制信号的星座特征,从而使参数估计精度的整体提升。
(2)方法定位性能渐近逼近相应的CRLB,说明了该方法的渐近有效性。
(3)相比于传统两步定位方法(MUSIC算法+Taylor级数迭代算法),三种DPD方法(未知信号波形,基于波形重构,信号波形完全已知)均能够给出更高的定位精度,这种性能优势尤其在低信噪比、小样本点数条件下表现明显,这一方面是由于单步直接定位方法本身所带来的好处,另一方面则是由于信号波形先验信息所带来的性能增益,而本文提出的方法在DPD方法的思想基础上,进一步利用了信号的调制特性和波形特征,从而获得了更高的定位精度。
(4)本文基于波形重构的MDPD方法在低信噪比下定位结果仍达不到波形先验已知的DPD算法定位精度,这是由于符号估计的误码率会对重构波形准确性产生影响,进而影响了定位精度。
(5)各种算法的定位精度均随着信噪比、频点数的增大而提高。
考虑到算法的实时性,最后在与节4.2相同仿真条件下比较本文算法的运行时间,图13给出了本文DPD算法和文献[9]中DPD算法运行时间随信号频域样本数变化的曲线。仿真实验环境为:Intel Core i5 CPU,16GB RAM,GTX1070 GPU,Windows64 位旗舰版,MATLAB 2010。
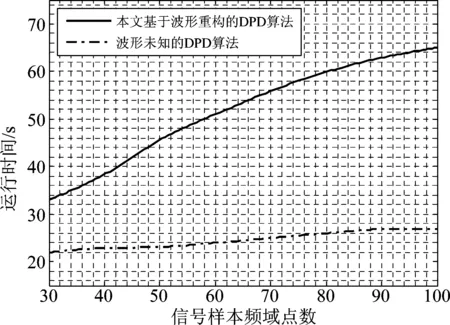
图13 算法运行时间随信号样本频域点数变化图Fig.13 The running time of the algorithms
实验表明,本文基于波形重构的DPD算法在提升精度的同时,也带来了计算复杂度的提升,但是随着计算机处理能力的增强,这部分计算时间不会影响算法工程应用的实时性。
5 结论
本文提出了一种基于多站联合波形重构的数字调制信号直接定位方法,利用最大似然准则和迭代算法对重构波形和辐射源位置参数进行联合估计。相关结论如下:
1)基于多站联合波形重构的MDPD方法定位性能渐近逼近参考的CRLB,说明了该方法的渐近有效性。
2)方法的定位精度要优于已有的未利用信号波形特征的DPD算法和传统两步定位法,性能接近理论最优定位精度,特别是在低信噪比条件下,方法性能优势明显。
3)采用迭代算法,以多次D维搜索代替了符号序列较长时的高维搜索,降低了对波形符号和辐射源位置参数进行联合估计的计算复杂度。
