以气缸为载体的高考题赏析

2018-07-25山东

教学考试(高考物理) 2018年2期

山东

庞超

从历年情况来看，每年都有以气缸为载体的高考题，且大多数时候与力学、热学等知识进行综合考查。

对于气缸类问题的解法，一般是应用理想气体状态方程，而理想气体的质量不变是该方程的适用条件。由于气缸类问题涉及气体、气缸、活塞、水银等多个研究对象，因此要善于从局部或整体选择相关的研究对象，将已知量与待求量分别列入相应的方程中，方能顺利求解。气缸类问题归纳起来主要有下文的五种类型，通过对气缸问题的归类解析，从中可以明显看出以气缸为载体的热学问题的解题思路。

一、“一团气”问题

这类问题的特点是活塞把气缸内部分气体封闭，题中气体状态的变化往往是“缓慢”进行的，而活塞的移动亦是缓慢的，因而可视为处于平衡状态。可利用力的平衡条件及理想气体状态方程联立求解。

【解析】设气缸的横截面积为S，活塞处于初始位置时气缸内气体的压强为p，p0为大气压强，则有

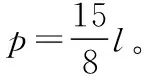
(1)在大活塞与大圆筒底部接触前的瞬间，缸内封闭气体的温度；

(2)缸内封闭的气体与缸外大气达到热平衡时，缸内封闭气体的压强。

【解析】(1)设初始时气体体积为V1，在大活塞与大圆筒底部刚接触时，缸内封闭气体的体积为V2，温度为T2，由题给条件得

V2=S2l

在活塞缓慢下移的过程中，用p1表示缸内气体的压强，由平衡条件有

p1S1+pS2=m1g+m2g+p1S2+pS1

解得p1=1.1×105Pa

故缸内的气体压强不变，由盖-吕萨克定律有

联立解得T2=330 K。

联立解得p′=1.01×105Pa。

二、“两团气”问题

此类问题在高考中多次出现，解决的方法是分别以两部分气体及活塞为研究对象，应用平衡条件确定两部分气体的压强的关系，而后应用理想气体状态方程求解。

1.气缸中的活塞直接将气体分隔为两部分的问题

在处理两部分气体相关联的气缸问题时，若被活塞隔开的气体状态发生变化，而各部分气体的质量是不变的，则此类问题可抓住三个关键：一是将每部分气体作为研究对象，明确其具体的气态变化过程和始末状态的参量(p、V、T)，列出相关的定质量理想气体状态方程；二是弄清各状态下各部分气体的压强关系，列出解题所需的辅助方程；三是当活塞截面积相等时，两部分气体的体积和为一定值，这是一个隐含条件，利用它可得到另一辅助方程，然后联立方程得出结果。

【例3】(2014·海南卷)一竖直放置、缸壁光滑且导热的柱形气缸内盛有一定量的氮气，被活塞分隔成Ⅰ、Ⅱ两部分；达到平衡时，这两部分气体的体积相等，上部气体的压强为p10，如图3甲所示，若将气缸缓慢倒置，再次达到平衡时，上下两部分气体的体积之比为3∶1，如图3乙所示。设外界温度不变，已知活塞面积为S，重力加速度大小为g，求活塞的质量。

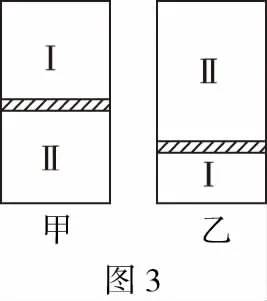
【解析】设活塞的质量为m，气缸倒置前下部气体的压强为p20，倒置后上、下部分气体的压强分别为p2、p1，由力的平衡条件有

气缸倒置过程中，两部分气体均经历等温过程，设气体的总体积为V0，由玻意耳定律有

【例4】(2016·海南卷)如图4所示，密闭气缸两侧与一U形管的两端相连，气缸壁导热；U形管内盛有密度为ρ=7.5×102kg/m3的液体。一活塞将气缸分成左、右两个气室，开始时，左气室的体积是右气室的体积的一半，气体的压强均为p0=4.5×103Pa。外界温度保持不变。缓慢向右拉活塞使U形管两侧液面的高度差h=40 cm，求此时左、右两气室的体积之比。取重力加速度大小g=10 m/s2，U形管中气体的体积和活塞拉杆的体积忽略不计。

【解析】设初始状态时气缸左气室的体积为V01，右气室的体积为V02；当活塞至气缸中某位置时，左、右气室的压强分别为p1、p2，体积分别为V1、V2，由玻意耳定律得

p0V01=p1V1,p0V02=p2V2

依题意有V01+V02=V1+V2

由力的平衡条件有p2-p1=ρgh

结合题给条件得V1∶V2=1∶1。

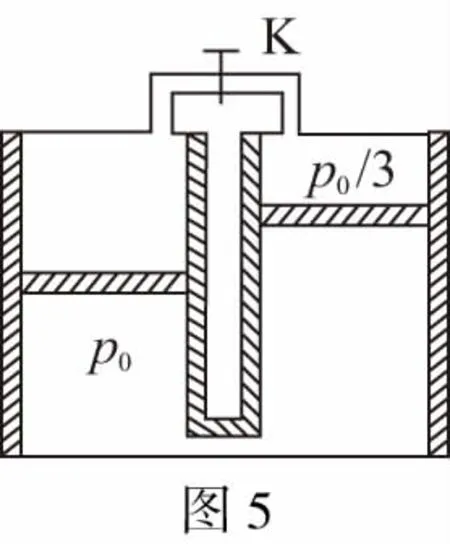
(1)恒温热源的温度T；

(2)重新达到平衡后左气缸中活塞上方气体的体积Vx。

(2)由初始状态的力学平衡条件可知，左活塞质量比右活塞的大。打开K后，左活塞下降至某一位置，右活塞必须升至气缸顶，才能满足力学平衡条件。

2.气缸中的活塞通过连杆将气体分隔成两部分的问题

【例6】(2014·上海卷)如图6所示，在水平放置的刚性气缸内用活塞封闭两部分气体A和B，质量一定的两活塞用杆连接。气缸内两活塞之间保持真空，活塞与气缸壁之间无摩擦，左侧活塞面积较大，A、B的初始温度相同。略抬高气缸左端使之倾斜，再使A、B升高相同温度，气体最终达到稳定状态。若始末状态A、B的压强变化量ΔpA、ΔpB均大于零，对活塞压力的变化量为ΔFA、ΔFB，则 ( )

A.A体积增大 B.A体积减小

C.ΔFA>ΔFBD.ΔpA<ΔpB

【例7】(2011·上海卷)如图7所示，绝热气缸A与导热气缸B均固定于地面，由刚性杆连接的绝热活塞与两气缸间均无摩擦。两气缸内装有处于平衡状态的理想气体，开始时体积均为V0、温度均为T0。缓慢加热A中气体，停止加热达到稳定后，A中气体压强为原来的1.2倍。设环境温度始终保持不变，求气缸A中气体的体积VA和温度TA。

【解析】设初态压强为p0，膨胀后A、B压强相等，设为pB,有pB=1.2p0

B中气体始末状态温度相等,则

得TA=1.4T0。

3.变异的气缸问题

【例8】(2016·全国卷Ⅲ)一U形玻璃管竖直放置，左端开口，右端封闭，左端上部有一光滑的轻活塞。初始时，管内汞柱及空气柱长度如图8所示。用力向下缓慢推活塞，直至管内两边汞柱高度相等时为止。求此时右侧管内气体的压强和活塞向下移动的距离。已知玻璃管的横截面积处处相同；在活塞向下移动的过程中，没有发生气体泄漏；大气压强p0=75.0 cmHg，环境温度不变。

p1=p0+(20.0-5.00)cmHg

解得h=9.42 cm。

三、气缸内气体变质量问题

气缸由于漏气导致质量发生变化，这类问题往往出现“缓缓”或“缓慢”这样的词语，这种情况需要做好活塞的受力分析，应用平衡条件处理问题。

【例9】(2015·海南卷)如图9所示，一底面积为S、内壁光滑的圆柱形容器竖直放置在水平地面上，开口向上，内有两个质量均为m的相同活塞A和B；在A与B之间、B与容器底面之间分别封有一定量的同样的理想气体，平衡时体积均为V。已知容器内气体温度始终不变，重力加速度大小为g，外界大气压强为p0。现假设活塞B发生缓慢漏气，致使B最终与容器底面接触。求活塞A移动的距离。

因为温度不变，对于混合气体有

(p1+p2)·V=pV′

四、气缸与力学规律结合类问题

气缸处于变速运动，这类问题需要做好受力分析，利用牛顿第二定律处理问题。

【例10】(2012·海南卷)如图10所示，一气缸水平固定在静止的小车上，一质量为m，面积为S的活塞将一定量的气体封闭在气缸内，平衡时活塞与气缸底相距L。现让小车以一较小的水平恒定加速度向右运动，稳定时发现活塞相对于气缸移动了距离d。已知大气压强为p0，不计气缸和活塞间的摩擦；且小车运动时，大气对活塞的压强仍可视为p0,整个过程温度保持不变。求小车加速度的大小。

【解析】设小车加速度大小为a，稳定是气缸内气体的压强为p1，活塞受到气缸内外气体的压力分别为

F1=p1S，F0=p0S

由牛顿第二定律得F1-F0=ma

小车静止时，在平衡情况下，气缸内气体的压强为p0，由玻意耳定律得p1V1=p0V

式中V=SL，V1=S(L-d)

五、有关气缸的实验问题

热学实验高考考查的不多，难度不大，但应该是今后考查的方向，应该引起重视。

【例11】(2012·上海卷)如图11所示，为“研究一定质量气体在压强不变的条件下，体积变化与温度变化关系”的实验装置示意图。粗细均匀的弯曲玻璃管A臂插入烧瓶，B臂与玻璃管C下部用橡胶管连接，C管开口向上，一定质量的气体被水银封闭于烧瓶内。开始时，B、C内的水银面等高。

(1)若气体温度升高，为使瓶内气体的压强不变，应将C管________(填“向上”或“向下”)移动，直至________；

(2)实验中多次改变气体温度，用Δt表示气体升高的温度，用Δh表示B管内水银面高度的改变量。根据测量数据作出的图线是 ( )

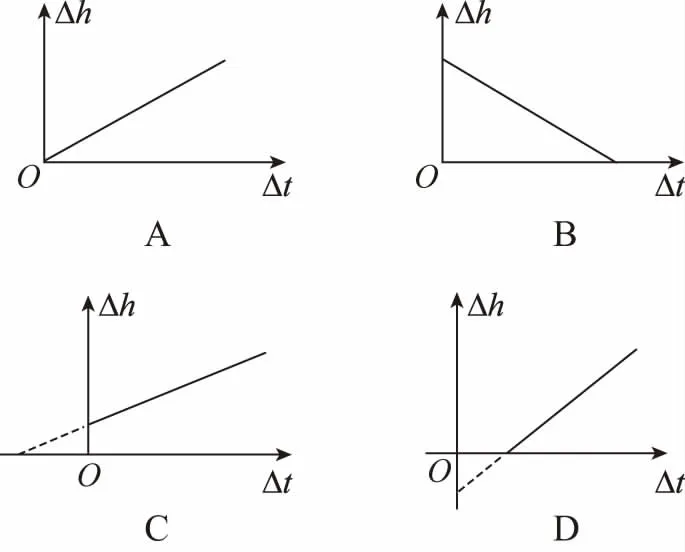
【答案】(1)向下，B、C两管内水银面等高 (2)A

【解析】(1)为使气体压强不变应使两侧水银面相平，由于温度升高，左侧气体体积膨胀，为使两边液面相平，需使右侧玻璃管向下移动。

(2)由于左侧发生的是等压变化，即

因此Δh- Δt图象是一条过坐标原点的直线，因此A选项正确。

【例12】(2017·全国卷Ⅲ)一种测量稀薄气体压强的仪器如图12甲所示，玻璃泡M的上端和下端分别连通两竖直玻璃细管K1和K2。K1长为l，顶端封闭，K2上端与待测气体连通；M下端经橡皮软管与充有水银的容器R连通。开始测量时，M与K2相通；逐渐提升R，直到K2中水银面与K1顶端等高，此时水银已进入K1，且K1中水银面比顶端低h，如图12乙所示。设测量过程中温度、与K2相通的待测气体的压强均保持不变。已知K1和K2的内径均为d，M的容积为V0，水银的密度为ρ，重力加速度大小为g。求：

(1)待测气体的压强；

(2)该仪器能够测量的最大压强。