动量定理与磁的综合应用
2018-07-25浙江
浙江
汪显和
动量是中学物理学的重要组成部分,动量中所涉及的一些物理概念和研究方法都是物理学中重要的知识点。而动量定理是物理学直接应用于生活实际的重要方法,充分体现物理学的实际应用价值,是高考考查的重要知识点。从2017年浙江省开始实行新高考,动量的内容从原来的自选模块变成为选考内容。分析连续五次选考试卷可以知道,2015年10月卷的第22题、2016年4月卷的第23题、2016年10月卷的第23题、2017年4月卷的第22题和2017年11月的第22题都涉及了动量定理的运用。高考是一种导向,是教育教学的方向标。在五次选考中都考查了动量定理的问题,又都是与磁场或电磁感应的综合应用问题,而且都赋予了前沿科技的背景知识,这充分体现了动量定理的重要性。本文从动量定理的模型出发,总结了动量定理在磁场和电磁感应中的应用模式。
一、动量定理内容与核心模型
1.动量定理的内容:
物体在一个过程始末的动量变化量等于它在这个过程中所受合外力的冲量,即FΔt=Δp。值得注意的是等式的左边是合外力的冲量,等式的右边是物体动量的改变量,等于末动量减去初动量。
2.核心模型:
模型一:瞬间作用力的模型
这类问题是物体在运动过程中与其他物体发生很短时间的相互作用(或称为瞬间相互作用),可利用动量定理求解在此过程中物体之间的相互作用力,通常针对于碰撞、打击和爆炸等问题。
【例题1】如图1所示,质量为m的小球沿光滑水平面运动,与竖直墙壁发生碰撞被反向弹回。已知碰撞前后的速度分别为v和v′,小球和墙壁的作用时间为Δt。求小球和墙壁作用过程中,墙壁对小球的作用力?

【解析】取向左方向为正方向,对小球研究,有:
F·Δt=mv′-(-mv)
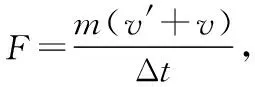
模型二:短时间积累的模型
这类问题通常是物体在力的作用下运动一段时间或产生一段位移,物体的速度发生了变化,可利用动量定理求解该类问题中相关的运动学的物理量,如时间、位移等。
【例题2】如图2所示,质量为m的物体沿光滑水平面运动,在水平拉力F的作用下,经过一段时间物体的速度从v变为v′,求力F的作用时间Δt?

【解析】取向右的方向为正方向,对物体研究,有:
-F·Δt=mv′-mv

二、磁场中的动量定理
磁场中的动量定理一般是针对带电粒子在运动过程中与其他物体发生碰撞的问题,由于此类问题中发生的相互作用时间很短,因此通常属于模型一。

(3)保持磁感应强度B1不变,求每秒打在探测板上的离子数N;若打在板上的离子80%被板吸收,20%被反弹回,弹回速度大小为板前速度大小的0.6倍。求探测板受到的作用力大小。


根据动量定理,其中被吸收的离子受到板的作用力大小为F1有F1Δt=Δp吸

因为打到板上各点速度随x轴成线性均匀变化,故

其中被反弹的离子受到板的作用力大小为F2,有
F2Δt=Δp反



根据牛顿第三定律可知,探测板受到的作用力的大小为
【总结】本小题是求离子与探测板碰撞产生的作用力,该力为瞬间作用,属于模型一。解决该类问题关键在于明确正方向,正确表示合外力的冲量和动量的改变量。带电粒子在磁场中运动过程中发生碰撞的问题通常属于该类,宜利用动量定理解决。
三、电磁感应中的动量定理
电磁感应中的动量定理通常是与安培力有关的,安培力在短时间的积累就是安培力的冲量。安培力中涉及电流,安培力的冲量中包含了电流和时间的乘积,也就是电荷量。而且电磁感应中的电流产生又是由磁通量的变化形成的,而涉及动量定理的问题中的磁通量变化通常是与位移有关。所以电磁感应中的动量定理问题一般是求电荷量和求导体棒运动位移的问题。

(3)t=0.22 s时闭合开关K,若安培力远大于重力,细框跳起的最大高度h=0.20 m,求通过细杆CD的电荷量。


又因为安培力远大于重力,所以可以忽略重力,写成FΔt=mv


【总结】这是电磁感应中求电荷量的问题,这里的电荷量是由于电流在短时间里通过电路积累的结果。由于电流的通过使导体受到了安培力,安培力在短时间里的积累就是安培力的冲量,需要利用动量定理来解决,属于前文中的模型二。此类问题中的电流一般都是变化的,由于这类问题中的过程非常短暂,可以用平均电流来代替变化的电流,由此就可以求得这段时间内通过导体的电荷量。
【牛刀小试】如图6所示,质量为M的U形金属框M′MNN′,静放在粗糙绝缘水平面上(动摩擦因数为μ),且最大静摩擦力等于滑动摩擦力。M′M、NN′边相互平行,相距为L,电阻不计且足够长,底边MN垂直于M′M,电阻为r。质量为m的光滑导体棒ab电阻为R,垂直M′M放在框架上,整个装置处于垂直轨道平面向上,磁感应强度大小为B的匀强磁场中。在与ab垂直的水平拉力作用下,ab沿轨道由静止开始做匀加速直线运动,经x距离后撤去拉力,直至最后停下,整个过程中框架恰好没动。若导体棒ab与M′M、NN′始终保持良好接触。
求:导体棒ab走过的总位移。

【解析】由题意可知当框架恰好不动时,导体棒速度最大,则有
FA=fm=μ(M+m)g
而FA=BIL
且I(R+r)=BLvm
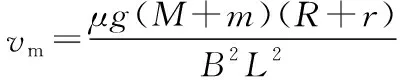
撤去力后导体棒在安培力作用下做减速运动,由动量定理可知
FAt=mvm


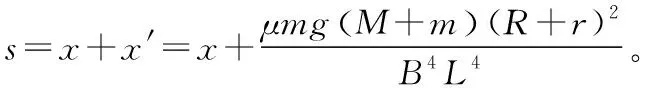
【总结】这是利用动量定理求导体棒运动位移的问题,属于模型二。在电磁感应的问题中涉及导体棒运动位移的问题一般用动量定理来解决,根据动量定理先求出电荷量,再结合法拉第电磁感应定律求得电荷量和位移的关系,最后联立起来求得导体棒运动的位移。

