基于L型阵列酉变换矩阵重构的二维DOA估计
2018-07-23王秀常青王耀力
王秀,常青,王耀力
基于L型阵列酉变换矩阵重构的二维DOA估计
王秀,常青,王耀力
(太原理工大学,山西 太原 030024)
二维空间信号波达方向(DOA)的估计是阵列信号处理的一个关键研究问题。经典的二维MUSIC算法固然精度高,但此算法需要二维谱峰搜索,运算较为复杂。提出一种用于L型阵列的二维DOA估计算法,通过矩阵重构使得阵列输出矩阵变为中心对称矩阵,再利用酉变换矩阵将其由复值矩阵变为实值矩阵。该方法可以直接得到目标参数,不需要谱峰搜索,使得运算量大大降低。相比于L型阵列适用的增广矩阵束(MEMP)算法,该算法可以估计更多信源的DOA,并能获得较高的分辨率。计算机仿真结果表明,该算法具有较高的DOA估计精度。
波达方向;L型阵列;酉变换矩阵;特征值;增广矩阵束算法
1 引言
波达角(direction of arrival,DOA)估计是阵列信号处理中的重要研究内容,在无线通信、声呐以及雷达等领域均有广泛应用[1-2]。一维(one-dimensional,1D)DOA估计目前已经发展相对成熟,最为经典的是多重信号分类(multiplesignal classification,MUSIC)算法和旋转不变子空间(estimating signal parameters via rotational in variance techniques,ESPRIT)算法[3]。近年来,二维(two-dimensional,2D)DOA 估计开始受到越来越多的关注和研究,许多阵列如 L 型阵列[4]、面阵[5]、均匀圆阵[6]和平行阵列[7]等被用来进行有效的2D参数估计。
L型阵列由于具有结构简单、易于传统算法移植以及更高 DOA 估计精度等优点[8],使得对于L型阵列的研究应用越来越多。与普通的线阵相比,L型阵列可提供全方位360°的DOA 估计并能达到较高精度的估计结果。与圆阵相比,除了数据处理方便,需要的运算量和存储量都较小,还可提高感兴趣方向的阵列孔径,在实际工程应用中具有较大的优势。金梁等[9-10]提出了时空DOA矩阵法,通过空时处理结合来进行DOA估计,该方法可用于其他阵列形状的二维DOA中。Tayem和Kwon[11]提出一种修正传播方法(modified propa-gate method,MPM)用于L型阵列的2D DOA估计,该方法克服了相位模糊问题,但参数匹配有效性差。Kikuchi等[12]提出了一种通过构造Toeplitz矩阵,利用交叉相关矩阵解决仰角匹配问题的方法,但该方法在角度过大时无法匹配。
Wei[13]提出一种新的多相干信号方位角和仰角的配对方法,利用两个信号源协方差矩阵构造的最小化代价函数实现,但估计性能还需要进一步改善。Ye等[14]提出了一种基于稀疏信号的L型阵列的DOA估计算法,该方法不需要角度配对也能实现较高的分辨率和估计精度。Yilmazer[15]将增广矩阵束(matrix enhancement and matrix pencil,MEMP)算法引入均匀矩形阵列的二维DOA估计中,通过对阵列接收信号构造增广矩阵来估计,只需要少量的采样数据就能得到较高精度的计算结果,但此算法阵元的利用率有所降低,且抑制噪声的能力较差。针对二维DOA估计的实用性问题,陈建[16]提出基于增广矩阵束的L型阵列二维DOA估计算法,该算法估计速度快、精度高、参数配对算法简单,具有较强的实用性。
本文分析了L型阵列的特点,提出了一种可用于L型阵列的二维DOA估计算法。该算法通过分析L型阵列的数据结构,利用反向单位矩阵重构方向矩阵,通过酉变换矩阵使得数据处理由复数域转换为实数域,通过特征分解得到信源的方位角和仰角,参数自动配对、运算量低。通过与MEMP算法和2D-MUSIC算法的仿真结果进行对比,验证了本文算法的有效性和优越性。
2 阵列信号模型
如图1所示为本文中所讨论的L型阵列,该阵列由分别位于轴和轴的阵元个数为的均匀线阵垂直构成,阵元间距为,假设有个不同方位的远场窄带信号源入射到该阵列上,入射角为(θ,ф),=1,2,...,,其中θ和ф分别为第个信源的方位角和仰角。假定文中涉及的噪声均为与信号不相关的加性高斯白噪声。

图1 L型阵列结构
阵列接收到的信源个数为,轴与轴上传感器个数均为,则轴和轴的接收信号分别为:
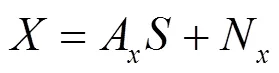

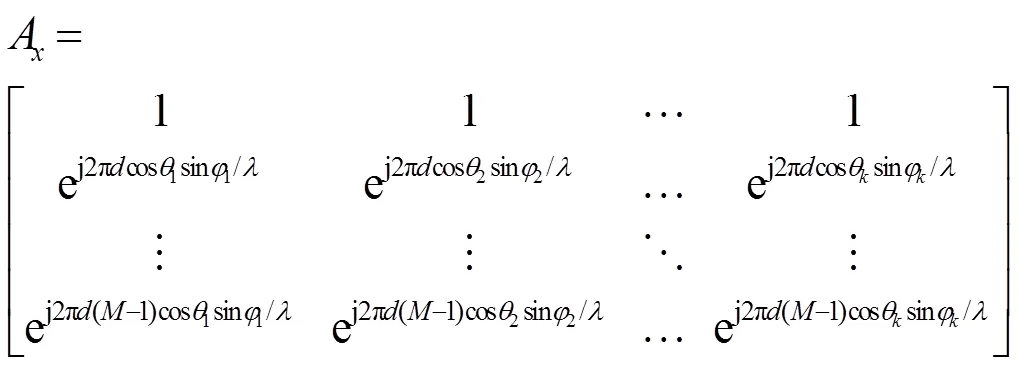

3 算法推导
L型阵列重构的输出矩阵0定义为:
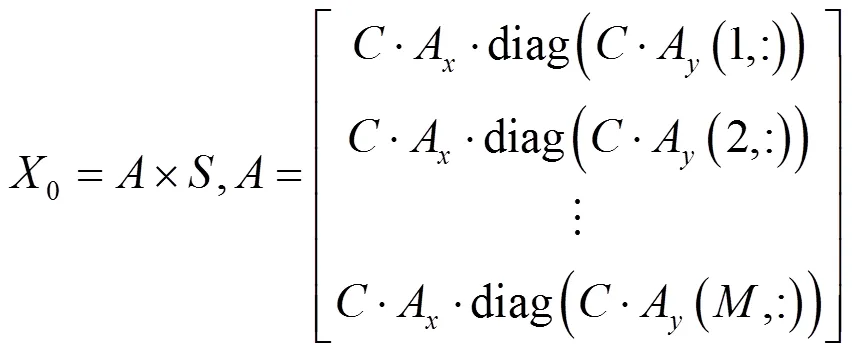
其中,为反向单位矩阵,此时的L型阵列输出矩阵为非对称矩阵,令:

X为0的自相关矩阵,构造矩阵X:

其中,X为X的共轭矩阵,X为中心对称矩阵,应用酉变化矩阵的思想,将X从复数域转换到实数域,酉变换矩阵Q(为反向单位矩阵)定义如下:
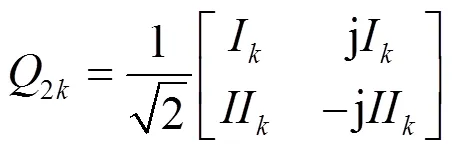
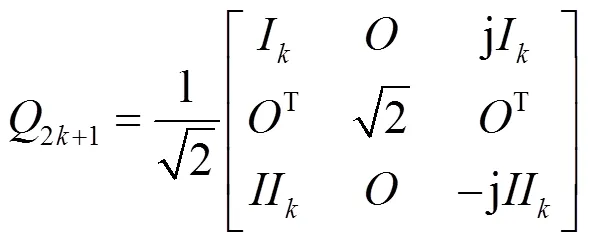
根据酉变化矩阵Q的定义,可以得到Q矩阵的性质如下:
(10)
从而,有式(11)成立:
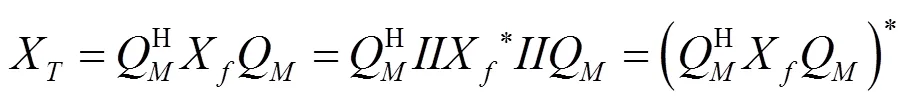
X与其共轭相等,由此证明X为实矩阵,虚部为零。因此,阵列输出矩阵重构为,定义如下:
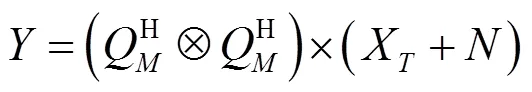
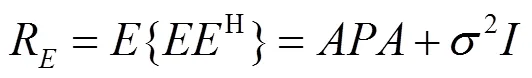
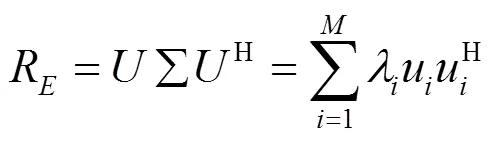
选择矩阵J、J定义如下:


分别选择矩阵的前-1项和后-1项。
现考虑一个信源,轴的方向矩阵可以表示为A,则有:

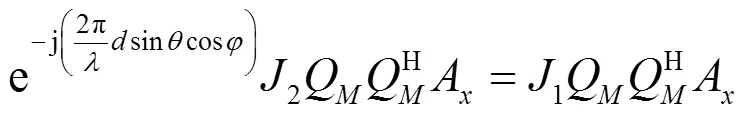
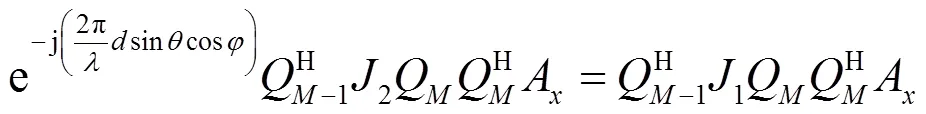
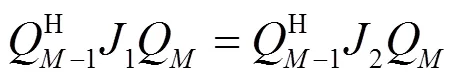
令:
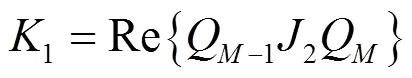
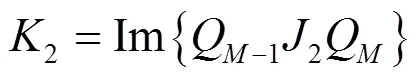
则有:
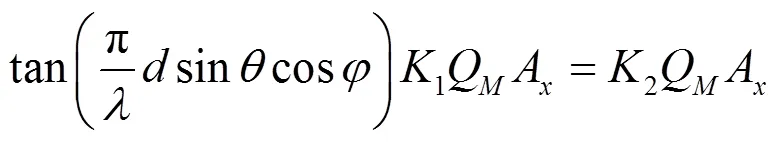
同样地,关于轴的方向矩阵A,在一个信源时,有:
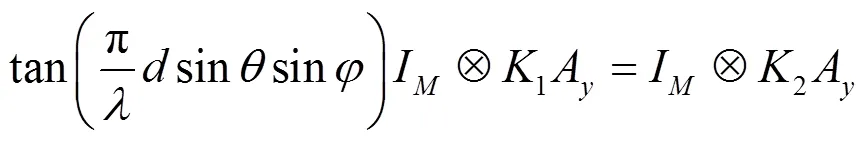
扩展到个信源时,则有:
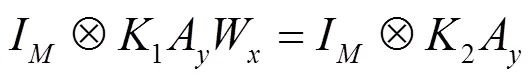
其中:
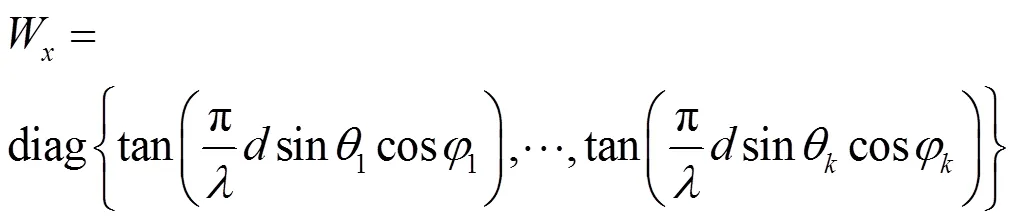
同样地,轴:
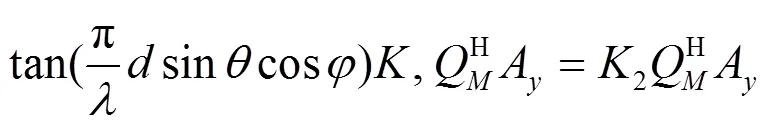
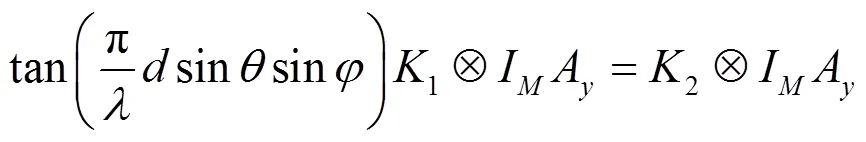
扩展到个信源时,则有:
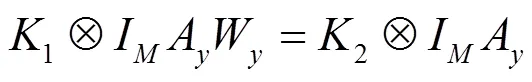
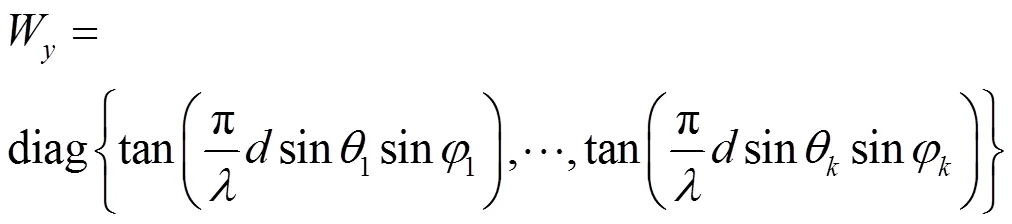
定义:

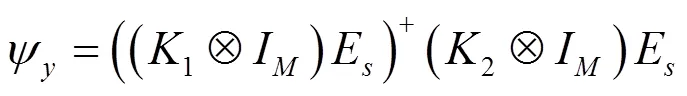
结合式(24)和式(28):
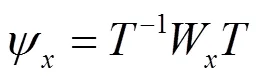
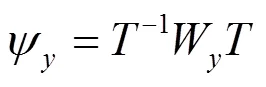
由于ψ和ψ有相同的矩阵,将ψ和ψ合并为:
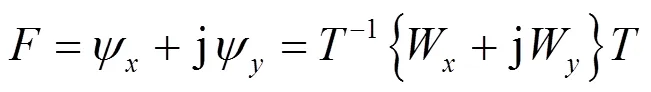
最后对得到的矩阵进行特征值分解,有:


可以得到入射角的方位角和俯仰角的估计值分别为:
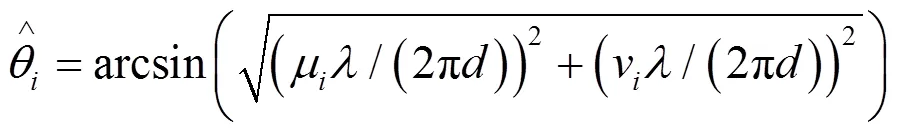
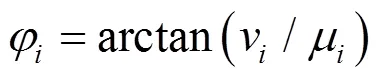
步骤1 计算阵列接收矩阵X并根据式(7)得到重构阵列的接收矩阵X;
步骤2 将得到的阵列接收矩阵X按照式(12)转换为实矩阵并构造矩阵;
步骤3 根据式(13)计算矩阵的协方差矩阵R,通过特征值分解得到信号子空间E;
步骤4 按式(33)和式(34)计算ψ、ψ,构造矩阵F=ψ+jψ;
步骤5 对矩阵作特征值分解,得到特征值为λ(=1,2,…,);
步骤6 根据式(38)和式(39)计算入射角的估计值。
4 实验仿真与性能分析
4.1 仿真实验
仿真参数:=8,即天线阵由轴和轴的8元均匀线阵构成,假设快拍数=200,信源数=3,信噪比为15 dB,3个入射角分别为(10°,15°)、(30°,35°)、(50°,55°),入射信号均为窄带不相关平面波。
(1)实验1
二维MUSIC算法是二维DOA估计的经典算法,此方法通过构造空间谱和二维谱峰搜索来实现信源估计,实验1通过2D-MUSIC算法对L型阵列进行DOA估计,其估计性能如图2所示。从图2中可以看出,3 个谱峰指示的入射角分别为(10°,15°)、(30°,35°)、(50°,55°),可见2D-MUSIC算法的估计精度很高,但此算法的计算量相当大,不适用于阵元数过大的情况。
数据结果采用SPSS 19.0进行统计分析,所得结果以“平均值±标准差”表示。运用LSD和Duncan's法检验进行多重比较。P<0.05认为有显著差异。

图2 2D-MUSIC算法下DOA估计结果
(2)实验2
分别采用增广矩阵束算法和本文算法估计入射角,蒙特卡洛试验次数设为500,仿真结果分别如图3、如图4所示。可以看出,两种算法都能估计出3个信源的入射角方向,但本文算法的计算结果较为集中,精度高于增广矩阵束算法,图5为入射角DOA估计的局部放大散点对比。从图5可以更为直观地看出本文算法性能远优于增广矩阵束算法。
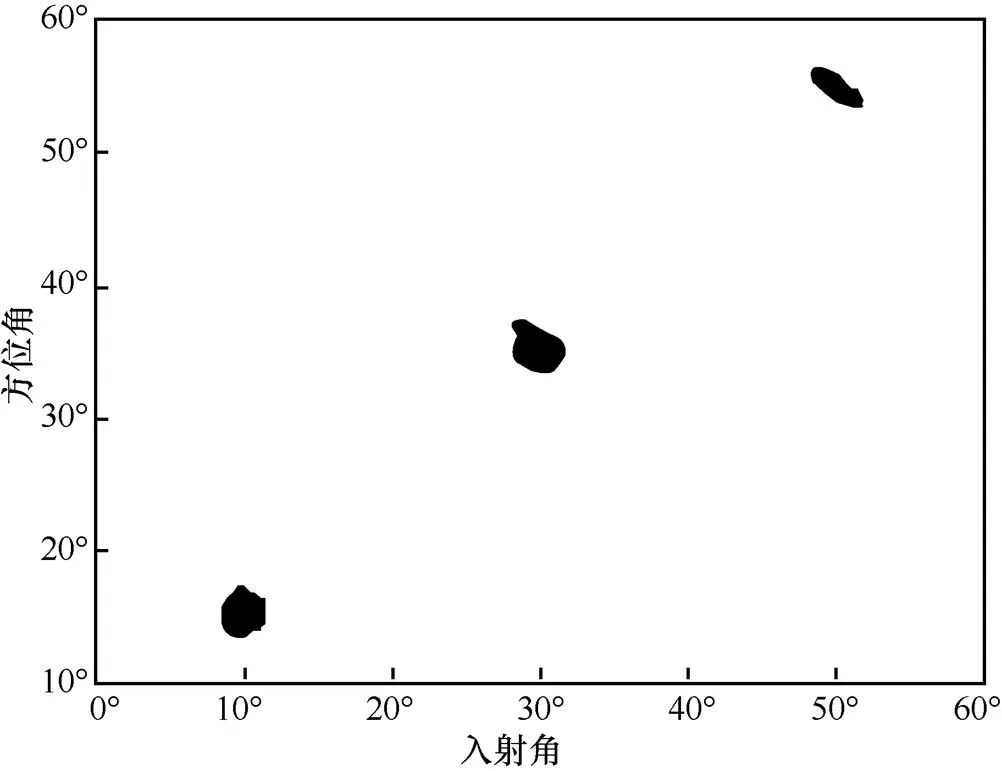
图3 增广矩阵束算法下DOA估计结果

图4 本文算法下DOA估计结果
4.2 性能分析
定义进行500次蒙特卡洛实验后方位角和仰角的联合均方根误差(root mean square error,RMSE)为:
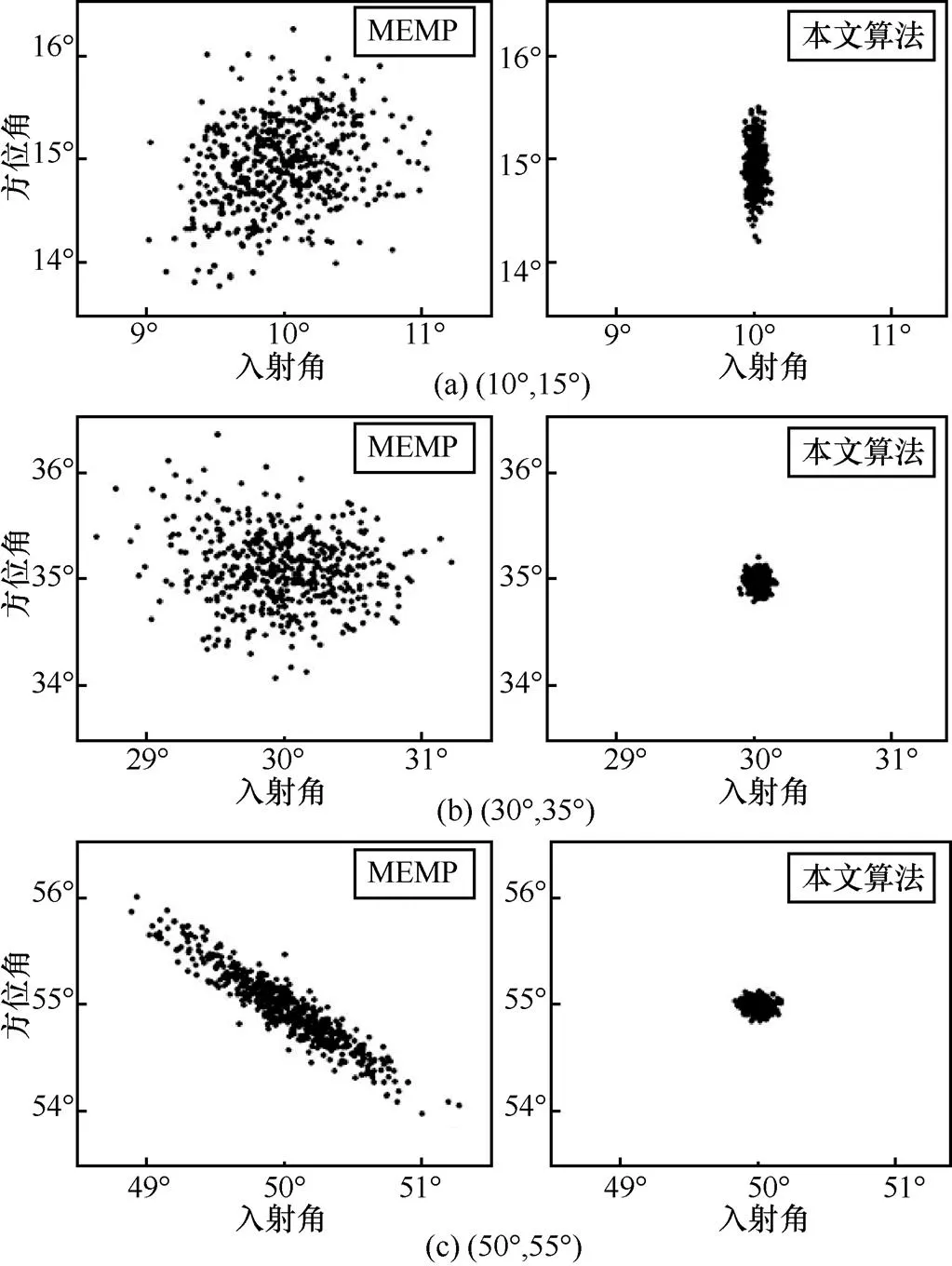
图5 两种算法DOA估计的局部放大散点图

图7表示在SNR=0 dB的条件下,令快拍数以步长100在区间[100 1 000]内取值,3种算法下二维DOA估计的均方根误差与快拍数变化的关系曲线。
从图6和图7可以看出,在信噪比和快拍数相同的情况下,本文算法的估计精度均高于MEMP算法。随着信噪比和快拍数的不断增大,本文算法的RMSE与2D-MUSIC算法的估计精度逐渐接近,这说明本文算法具有较强的顽健性。

图6 RMSE随信噪比的变化曲线
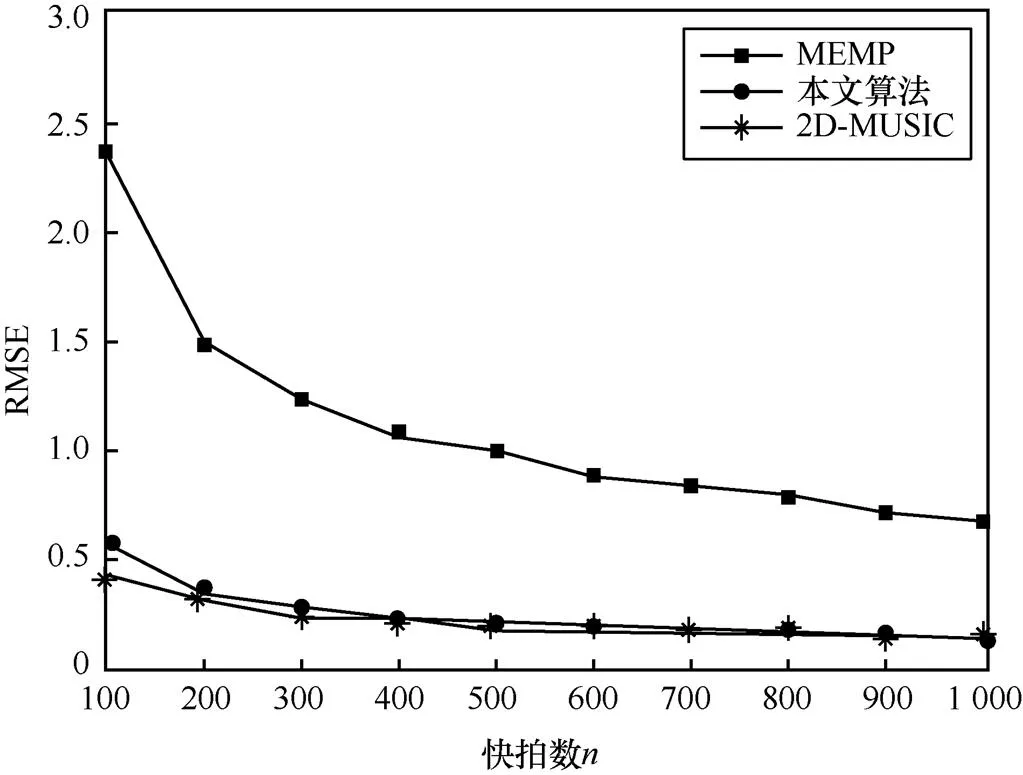
图7 RMSE随快拍数的变化曲线
5 运算结果分析
由算法推导过程可知,算法运算时间区别主要由信源数和阵元数决定,与快拍数和信噪比无关。假定信源数为3,3种算法单次运算时所需时间随阵元数的变化情况见表1。
由表1可知,阵元数<20时,增广矩阵束和本文算法的计算时间较为接近,当阵元数>20以后,增广矩阵束和本文算法的计算时间差距逐渐增大,本文算法由于输出阵列矩阵重构,运算时间略大于增广矩阵束算法,但总体来说,本文算法通过酉变换矩阵将协方差矩阵由复数域变为实数域,在达到较高精度的基础上,运算量也远小于传统2D-MUSIC算法。
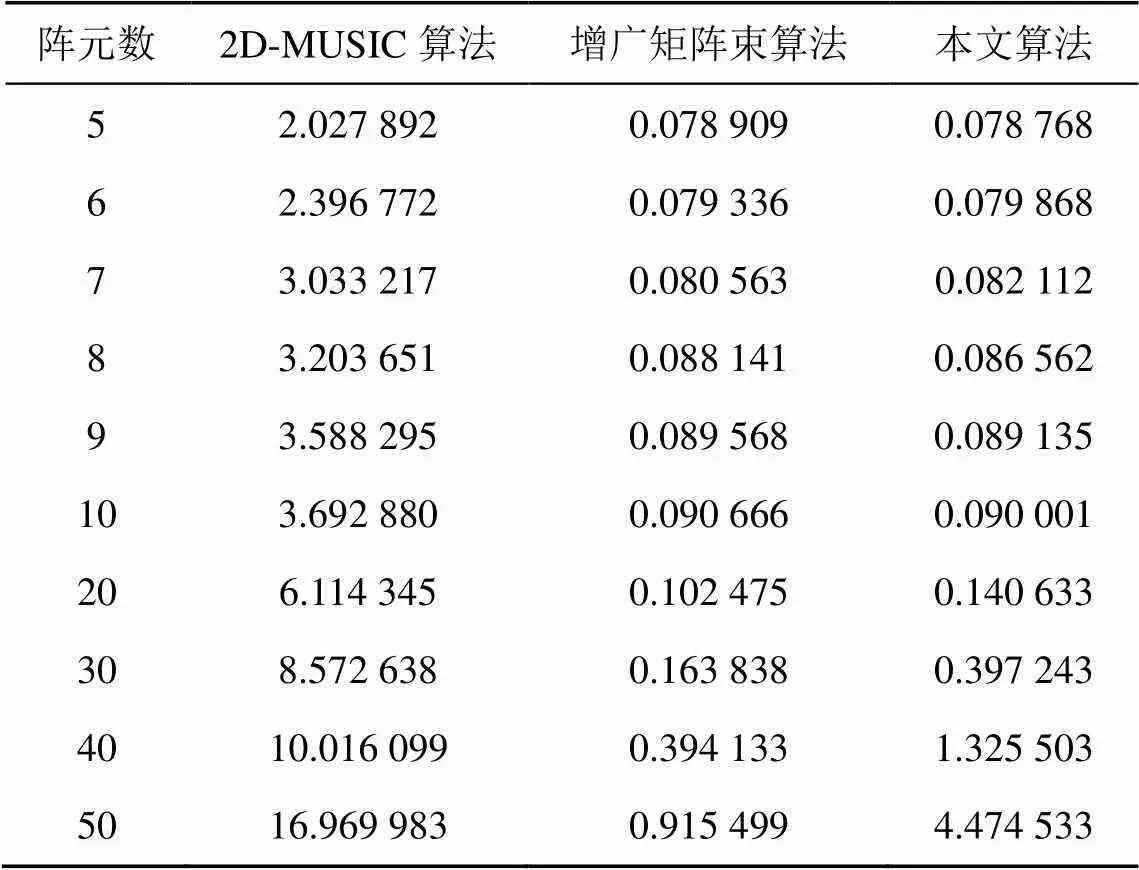
表1 各种方法下DOA估计耗时随阵元数的变化(单位:s)
6 结束语
L型阵列是二维DOA估计重要研究内容。传统实值矩阵处理要求信号阵列模型必须为中心对称阵列,多适用于均匀圆阵和面阵。本文通过反向单位矩阵和自相关矩阵重构,得到变为中心对称矩阵的阵列输出矩阵,通过酉变换矩阵将输出矩阵由复值转为实值,降低了运算复杂度,突破了信号阵列模型必须为中心对称阵列的局限性,其计算精度高于增广矩阵束算法并接近传统的2D-MUSIC 算法。但此算法目前只适用于轴和轴阵元数相等的L型阵列,当轴和轴阵元数不相等时,本文算法的计算精度将会大大降低,这也是本文算法的不足之处,还有待继续研究改进。
[1] JUNG T J, LEE K K. Closed-form algorithm for 3-D single-source localization with uniform circular array[J]. IEEE Antennas Wireless Propagation Letters, 2014, 13(1): 1096-1099.
[2] 李婷. 二维谱估计算法的空间探测性能分析及验证[J].电信科学, 2016, 32(5): 173-178.
LI T. Analysis and verification on space probe performance of 2-D spectrum estimation algorithm[J]. Telecommunications Science, 2016, 32(5): 173-178.
[3] 吴秀芬. 宽带阵列信号DOA估计方法研究[D]. 南京: 南京大学, 2013.
WU X F. Research on wideband array signal DOA estimation[D]. Nanjing: Nanjing University, 2013.
[4] GU J F,ZHU W P, SWAMY M N S.Joint 2-D DOA estimation via sparse L-shaped array[J]. IEEE Transactions on Signal Processing, 2015, 63(5): 1171-1182.
[5] ZHANG W, LIU W, WANG J, et al. Computationally efficient 2-D DOA estimation for uniform rectangular arrays [J]. Multidimensional Systems & Signal Processing, 2014, 25(4): 847-857.
[6] 穆昌, 姚俊良, 蔡振合. 三维MIMO阵列空间相关性分析[J].电信科学, 2015, 31(1): 1-6.
MU C, YAO J L, CAI Z H. Spatial correlation analysis of 3D MIMO array[J]. Telecommunications Science, 2015, 31(1): 1-6.
[7] 张小飞, 张立岑, 孙华普, 等.双平行线阵中基于Euler变换传播算子的二维DOA估计算法[J]. 南京航空航天大学学报, 2015, 47(3): 324-331.
ZHANG X F, ZHANG L C, SUN H P, et al. Two-dimensional DOA estimation algorithm for two parallel linear arrays via Euler transformation and propagator method[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(3): 324-331.
[8] GU J F, ZHU W P, SWAMY M N S. Performance analysis of 2-D DOA estimation via L-shaped array[C]//2012 25th IEEE Canadian Conference on Electrical & Computer Engineering (CCECE), April 29-May 2, 2012, Montreal, Canada. Piscataway: IEEE Press, 2012: 1-4.
[9] 金梁, 殷勤业. 时空 DOA 矩阵方法[J].电子学报, 2000, 28(6): 8-12.
JIN L, YIN Q Y. Space-time DOA matrix method[J]. Acta Electronica Sinica, 2000, 28(6): 8-12.
[10] 金梁, 殷勤业. 时空 DOA 矩阵法的分析与推广[J]. 电子学报, 2001, 29(3): 300-303.
JIN L, YIN Q Y. Analysis and generalization of space-time DOA matrix method[J]. Acta Electronica Sinica, 2001, 29(3): 300-303.
[11] TAYEM N, KWON H M. L-shape2-dimensional arrival angle estimation with propagator method[C]//VTC-2005, May 30-June 1, 2005, Stockholm, Sweden. Piscataway: IEEE Press, 2005: 1622-1630.
[12] KIKUCHI S, TSUJIH, SANO A. Pair-matching method for estimating 2-D angle of arrival with a cross-correlation matrix[J]. IEEE Antennas and Wireless Propagation Letters, 2006, 5(1): 35-40.
[13] WEI Y S, GUO X J. Pair-matching method by signal covariance matrices for 2D-DOA estimation[J]. IEEE Antennas Wireless Propagation. Letters, 2014(13): 1199-1202.
[14] TIAN Y, LIAN Q S, XU H. Sparse-reconstruction-based 2-D angle of arrival estimation with L-shaped array[J]. International Journal of Electronics and Communications, 2017(72): 162-165.
[15] YLIMAZER N, SARKAR Y K. 2-D unitary matrix pencil method for efficient direction of arrival estimation[J]. Digital Signal Processing: A Review Journal, 2006, 16(6): 767-781.
[16] 陈建. 二维波达方向估计理论研究[D]. 长春: 吉林大学, 2006.
CHEN J. Theoretical study on two-dimensional direction of arrival estimation[D]. Changchun: Jilin University, 2006.
Two-dimensional DOA estimation of unitary transformation matrix reconstruction based on L-shaped array
WANG Xiu, CHANG Qing, WANG Yaoli
Taiyuan University of Technology, Taiyuan 030024, China
The estimation of the direction of arrival of two-dimensional space signals is the key problem in the field of array antennas. Although the traditional two-dimensional MUSIC algorithm has high precision, it needs two dimensional spectrum peak search and has a large amount of operation. A two-dimensional DOA estimation algorithm for L-shaped array was proposed. The output matrix was transformed from a complex value matrix to a real value matrix by matrix reconstruction and a unitary transformation matrix. This method could directly get the elevation angle of the target without conversion, which greatly reduced the amount of operation. Compared with the matrix enhancement and matrix pencil algorithm for L-shaped array, this algorithm could estimate more targets’DOA. The results of simulation show that the algorithm has a high accuracy of DOA estimation.
direction of arrival, L-shaped array, unitary transformation matrix, eigenvalue, matrix enhancement and matrix pencil algorithm
TN911.7
A
10.11959/j.issn.1000−0801.2018208
2018−01−05;
2018−06−29
常青,changqing@126.com
王秀(1993−),女,太原理工大学硕士生,主要研究方向为传感器阵列信号处理。

常青(1975−),男,博士,太原理工大学副教授、硕士生导师,主要研究方向为嵌入式个人/家庭服务器、嵌入式系统等。
王耀力(1965−),男,博士,太原理工大学副教授、硕士生导师,主要研究方向为人机视觉分析与处理、嵌入式系统电路设计理论等。

