“测度”不同，“法”亦有别——谈几何概型的分类求解

☉江苏省石庄高级中学 顾永建

概率问题在高考中越来越凸显出它的重要地位，其中几何概型又因其与现实生活联系密切，与几何论证和计算有着密切关系，也日渐成为考查的一个热点.古典概型及几何概型中，基本事件的发生都是等可能性的，但是求解的方法是有差异的，本文主要从“测度”为长度、角度、面积、体积等几个方面进行阐述.

一、“测度”与长度有关

如果试验的结果所构成的区域的几何测度可以用长度表示，那么就可以判断需要利用几何概型的概率计算公式来求概率，即有解决此类问题的一般思路是将题给条件放置在数轴上或者转化为线段进行分析，求出所求事件对应的长度d，及全部事件对应的长度D，然后代入上述公式进行计算.

例1已知a∈［0，6］，使得函数f（x）=lg（ax2-ax+1）的定义域为R的概率为______.

解析：根据对数函数以及二次函数的性质求出使得“函数f（x）的定义域是R”的a的范围，根据区间长度的比值求出满足条件的概率的值.若f（x）=lg（ax2-ax+1）的定义域为R，则函数g（x）=ax2-ax+1＞0恒成立，a=0时，显然成立，a≠0时，只需

乍看本题求解的思路还是比较迷茫的，不能明确是古典概型还是几何概型.根据a∈［0，6］及函数f（x）=lg（ax2-ax+1）的定义域为R，可以确定所求概率模型为几何概型，“测度”为参数a的取值区间长度.同时，本题还考查了对数函数的定义域、对数的性质以及二次函数的性质.

二、“测度”与面积有关

当题目中涉及面积问题，或者需要用两个连续变量来描述某个随机事件时，可以考虑用几何概型的概率计算公式探究.此类问题求解的关键是正确构造出与随机事件对应的几何图形，求出相关区域的面积，即测度d和D，然后代入上述公式进行计算表述.

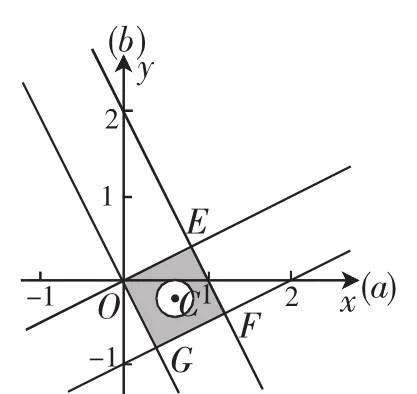
图1

本题的探究思路是利用向量的数量积知识将不等式进行转化，然后根据转化得到的不等式组作出相应的区域，解题的关键是准确地求出两个区域的面积，然后再利用公式进行计算.其中对于涉及到两个变量的问题，常利用平面直角坐标系把实际问题转化为数学问题来探究，求解过程中要注意平面图形面积的求解技巧.

三、测度与体积有关的几何概型

设有两个区域d，D满足d⊂D，若D为三维空间，点p落在D每一处都是等可能的，且点p落在区域d的概率与体积有关，可以选择体积作为区域的测度，考虑利用几何概型的概率计算公式进行求解.

例3 已知在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是正方形，PA=AB=2，在该四棱锥内部或表面任取一点O，则三棱锥O-PAB的体积不小于的概率为______.

解析：根据题意画出图形，结合图形利用对应的体积比值求出对应的概率.如图2所示，AD，BC，PC，PD的中点分别为E，F，G，H，当点O在几何体CDEFGH内部或表面上时在几何体CDEFGH中，

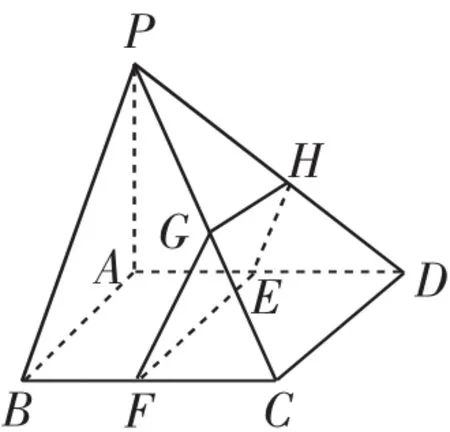
图2

通过分析题意，本题的“测度”为几何体的体积，为了求出所有符合条件的点，需要找出一个符合条件的界点，这里体现了点、线、面、体的相互转化.

四、测度与角度有关的几何概型

在求与角度有关的几何概型时，要注意准确找到D和d所表示的角度的值，同时要注意“角度”与“长度”的区别.

解析：因为在∠BAC内作射线AM交BC于M，故考虑用角度作为测度来求解.如图3所示，射线AM在∠BAC内是等可能分布的，当AM与高AE重合时，BM=1，故满足BM＜1的射线AM在∠BAE内，于是D=∠BAC=180°-（60°+45°）=75°，d=∠BAE=90°-

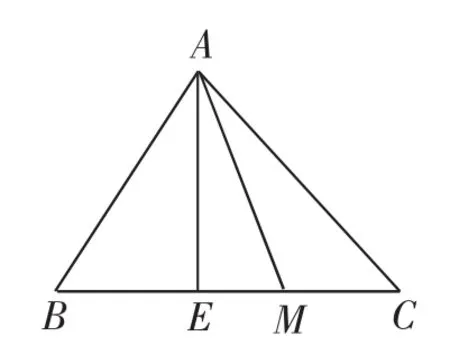
图3

本题容易出现错解，认为“测度”为线段的长度.在阅读题目时，要注意对语句的正确理解，尤其是背景相同的通源变式题.

五、用随机模拟求几何概型

对于一些区域的面积计算比较困难的几何概型问题，可以采用计算器或计算机产生随机数进行模拟计算.

例5 在长和宽分别为8和4的矩形区域内有一椭圆，长轴长和短轴长分别为4和2，则向矩形区域内投点，求点落在椭圆内的概率.

解析：在直角坐标系内画出矩形和椭圆的图像，用随机模拟法求得s的近似值.（1）利用计算器或计算机产生两组（0，1）区间上的随机数a和b，a=RAND，b=RAND.

（2）进行伸缩和平移变换：x=8a-4，y=4a-2（其中x，y分别为随机点的横坐标和纵坐标，即-4≤x≤4，-2≤y≤2）.（3）向矩形区域内投N个点，数出落在椭圆内的如，做10000次试验，即N=10000，模拟得到N1=6272，所

几何概型的概率计算公式与古典概型的概率计算公式形式上类似，它们的求解思路相同，都是“比例解法”.同时几何概型具有无限性、等可能性的特点.在几何概型中，概率大小与区域形状、位置无关，只与测度有关，因此关于测度的确定至关重要，需要对测度的类型进行精确定位.J