微课教学在高中数学中的应用

☉江苏省吴江高级中学 李保楠

微博、微信、微电影等应运时代发展的产物将现代社会标上了“微时代”的鲜明特征，伴随数字化教学应运而生的微课教学为学生的数学学习起到了很好的辅助作用，微课教学明显在提升学生学习兴趣的同时也开启了高中数学学习多元化的新局面.本文着眼于微课在高中数学课前预习、课堂导入、重难点突破、变式、课后复习等阶段的应用进行了粗浅的思考.

一、微课的简述

针对某个知识点进行专门性训练或解释的视频或音频是微课呈现的主要形式，多媒体技术是微课呈现的主要手段，实际教学中，以教学设计思想为基础的微课内容一般都呈点状、碎片状.微课这一新时期新技术的产物对于课堂教学来说是极为有效的补充，学生进行个性化与深度化学习的过程需要微课这一重要的形式与途径.教师一般会运用手机、相机、DV等设备录制视频或音频进行具体的微课教学.

二、微课的应用

1.预习环节的应用

预习环节中的微课设计应以学生不易掌握的重难点为主，让学生在充裕的思考中领会新知识的意义并记录不能理解的知识点，这对于后续课堂教学中的师生交流、生生交流环节来说是最有意义的，学生根据自己预习的感悟在课堂上进行释疑解难、合作交流，在真正实现先学后教教学形式的同时也深化了学生对重难点的理解.

例如，直线与圆锥曲线的位置判断这一内容的微课课件可以让学生在预习中知道判断两者关系的方法，理解直线与椭圆相离、相切、相交这三类关系，能够对直线被椭圆所截得的弦长公式形成初步的掌握与运用：设A（x1，y1），B（x2，y2）为椭圆上的两个点，|AB|叫做椭圆的弦长.回忆并运用两点间的距离公式进行化简整理得出弦长公式AB的斜率）.学生在该课内容的教学之前进行反复的微课学习可为课堂学习作好充足的准备.

2.课堂导入环节的应用

例如，数列求和的实际教学中，教师可以首先将探究的课题设计好，然后根据课题与具体课时进行教学目标与重难点的制定，然后在课堂教学中创设出问题情境以激发学生产生疑惑并进行自主探究.情境如下：世界古建筑七大奇迹之一的泰姬陵用的材料主要是纯白大理石，陵寝这一三角形图案则镶嵌了大量的宝石，大量大小相同的宝石镶嵌而成的陵寝共有100层，具体形状如图1所示，教师伴随图片的展示进行提问：大家能够算出这一图案中宝石的数量吗？

图1

课堂教学中所要讲解的知识在这一情境问题中被有效地引导了出来，借助多媒体技术并以微课形式呈现的问题情境不仅将学生的注意力牢牢地吸引了过来，学生也在问题的研究与探索中展现出了更加浓厚的兴趣，伴随该建筑图案视频的播放，教师可以这样提问：大家看到这个问题情境可曾联想到哪一些数学问题呢？学生在这一问题的启发与思考中会提出新问题，例如图案中的宝石在镶嵌时可有什么规律呢？例如1+2+3+…+100又应该怎样求解呢？高斯算法能用来求解等差数列前n项和吗？教师在启发学生提出问题、帮助学生梳理问题的同时即可提出本课的学习目标.随后，教师可以组织学生进行小组合作讨论，并在学生取得一定讨论成果后组织群体讨论，明确各小组的课堂任务并鼓励学生展示各小组的讨论成果，使学生能够在一系列的问题探讨与分析之后得出等差数列前n项和的公式.

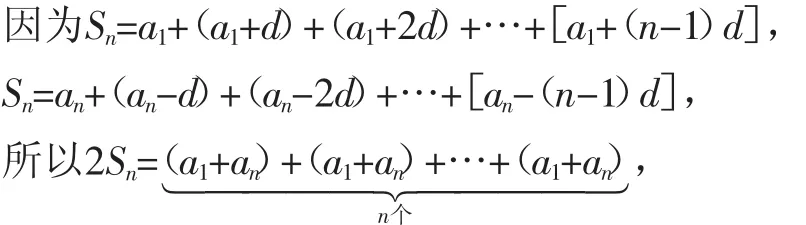
此时教师还应将一些相关知识补充给学生，学生之前学过an=a1+（n-1）d，所以，等差数列的另一种变形公式

3.突破重难点环节的应用

课堂教学的核心环节正是教学重难点的有效突破，学生在生动的微课预习中往往会产生很多的感受与体验，带着这些体验与感受进行课堂学习往往会有更多的生成性知识.课堂导入环节中的微课教学在有效激发学生学习兴趣的同时能帮助学生形成有效的思考、体验与感悟，课堂教学重难点突破环节中的微课教学能使抽象的数学知识变得更加具体，学生在化难为易、化复杂为简单的微课教学中能够更加轻松、容易地理解知识的重难点，教学重难点的顺利突破不仅使得宝贵的数学课堂教学容量得以有效增加，还在有效节约课堂教学时间的同时大大提升课堂教学的质量与效率.

例如，直线与圆锥曲线这一平面解析几何教学中的核心内容一直是近年来高考数学题反复考查的热点，直线与圆锥曲线的位置判断这一内容的教学主要是让学生在学习中学会判定直线与圆锥曲线位置关系的方法，方程思想、分类讨论思想以及数形结合思想、等价转化、点差法等诸多思想方法都是这一内容中需要学生掌握并能灵活运用的内容.因此，教师在实际教学中可以将每个知识点的讲解制作成微课视频播放给学生学习，使学生能够不断积累，提升归纳、推理以及判断的能力并保持数学学习的兴趣.

4.变式训练环节中的应用

教师在实际教学中有意识地针对一些问题引导学生尝试改变条件、结论等形式进行反复编题，能使学生在众多的变化与思考中逐步形成更好的数学思维并牢固掌握常用的数学解题方法.

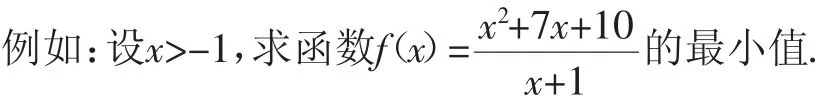
教师在给出这一题目之后对学生进行了提问启发：题中所给函数是什么函数呢？该函数的最值应该怎样去求？要求函数的值，大家会联想到哪些知识呢？

学生在教师的启发性提问下一一思考并给出这样的结果与结论：题中所给出的函数为分式函数，要求分式函数的最值应该首先对其进行变形，函数变形后得到f，学生在函数式的变形中会很快联想到基本不等式，教师随着学生的思维进行顺势引导，学生很快从推导出，当且仅当x+，也就是x=1时等号成立，所以，当x=1时，函数有最小值9.

该题解出后的变式训练对于学生来说是更加重要的，因此，教师此时应对学生进行启发式提问：大家认为还有哪些题目也可以这样变形呢？然后引导学生对问题进行小组讨论并将学生讨论的结果以微课形式展示出来，教师再及时根据学生的讨论结果帮助学生一起进行综合分析、归纳与总结，这样一个问题促进一类问题的模式对于学生的思维发展来说意义重大，学生在有意义的自主探究、知识剖析、习题解析中发现并提出问题能够更好地促进自身数学思维的快速发展.

5.课后巩固环节的应用

事先录制的视频或音频是学生根据自身学习需要随时可以重复观摩学习的，学生的课余时间因此得到了最为充分的开发与利用，反复多次的微课学习能使学生将课堂上未能完全理解的知识进行重复思考与揣摩，在补充、完善学生理解的同时还能更好地加深学生对知识的记忆，学生思维得到训练、拓展的过程中还会对数学知识形成更有意义的拓展与创新.

由此可见，微课是高中数学高效课堂实施的有效途径，各个具体教学环节中的微课渗透不仅能够为学生的学习建立牢固的基础与铺垫，还能及时帮助学生在学习需要时进行及时地补充与完善.结合学生特点与教材特色的划时代微课教学模式不仅实现了学生的个性化学习，还使得现代教育的教学方法得到了不断的更新.学生在微学习的长期渗透中能够逐步培养出数学的大智慧，在微知识的长期积累中能够更好地理解知识中的内涵，并因此树立起健全的人格以适应社会迅猛发展的需求.H