高中数学复习课教学的新视角

☉江苏省宜兴市丁蜀高级中学 宋 卫

高中数学复习课教学怎样才能保持课堂鲜活的生命力是广大高中数学教师一直研究的问题.事实上，教师在复习课教学中仅仅关注知识的回顾和整理是远远不够的，数学思想方法的沟通才是复习课教学中最为重要的内容.因此，教师在复习课教学中首先应清楚课中各部分内容的重要程度，在课堂教学中做到重点突出、有的放矢.另外，教师可以在复习教学中立足小切口设计出形式多样的复习教学并因此实现连点成线、以线带面的复习效果.同时，教师还可以不断变换视角对复习的内容进行新的思考与设计，使学生对复习活动保持持久的新鲜感与动力.本文是笔者在观摩一节公开课后，结合执教教师在直线方程及其应用这一节的教学内容及所获得的认识与理解来展现以下各教学环节.

一、创设情境，引入课题

1.直线方程的各种形式，如表1.

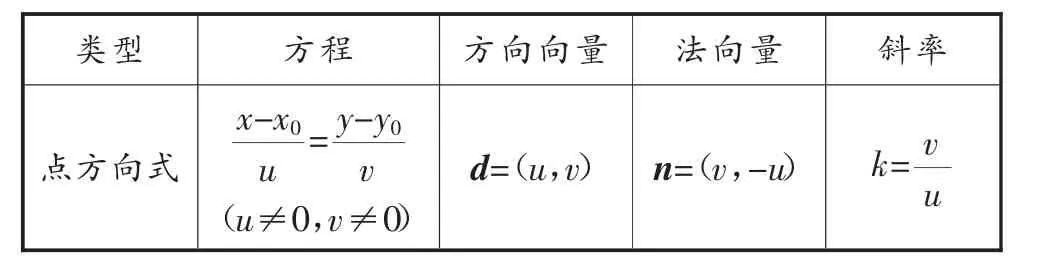
表1

点 法 向 式 a（x-x0）+b（y-y0）=0 d=（b，-a） n=（a，b）（存在时）k=-a b点斜式 y-y0=k（x-x0） d=（1，k） n=（k，-1） k斜截式 y=kx+b d=（1，k） n=（k，-1） k一般式ax+by+c=0（a，b不同时为零）d=（-b，a） n=（a，b）（存在时）k=-a b

2.直线倾斜角和斜率的关系，如图1.

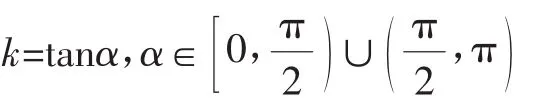
二、分析例题，探求方法

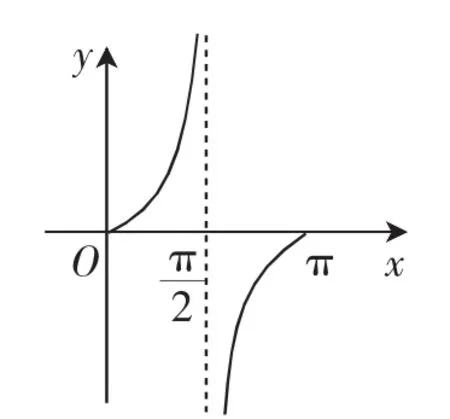
图1

例题 如图2，已知△ABC的三个顶点A（0，0），B（3，4），C（12，5），求：

（1）BC边所在直线的点方向式方程；

（2）BC边上的中线AD所在直线的一般式方程；

（3）BC边上的高AE所在直线的方程.

图2

解：（1）直线BC的一个方向向量是d=（9，1），直线BC经过点B（3，4），因此BC边所在直线的点方向式方程是

（3）直线AE的一个法向量是B—→C=（9，1），直线经过A（0，0），因此直线AE的点法向式方程是9（x-0）+1（y-0）=0，即9x+y=0.

设计意图：这是来自于学生作业题中的一个典型练习，教师在课堂上首先请一位学生上黑板板演并要求其他学生也在下面独立解决，大多数学生都能较快地解决此题.教师在学生完成解题之后又引导学生对直线方程的常用求解办法进行了总结与表述，使学生在总结归纳的过程中很好地理解了直线方程的获得需要满足两个条件：条件一即题中条件涉及的点应该是不同的两个点；条件二即求解直线方程需满足一个点与一个可以刻画直线方程的量.

教师紧接着又提出以下问题：我们在三角形中还学过哪些重要的线呢？大家想一想还能求出哪些线的方程呢？学生的钻研劲头在教师的提问中一下子得到了激发，从而也使变式探究异常精彩，学生经过一定的合作交流以后作出了以下变式：

变式1：在△ABC中，求∠A的平分线所在直线的方程.

解：∠A的平分线所在直线的方程：7x-9y=0.

变式2：过A作直线l，l将△ABC的面积分成13∶5两部分，求直线l的方程.

解：直线l的方程为85x-171y=0或7x-9y=0.

（教师在讲解过程中引导学生大胆发表自己的意见，使学生在阐述自己思路的过程中对直线方程的求解方法获得了再一次的体验与感悟，同时要求学生在分类讨论的过程中能够画出图形并感悟各条件之间的关系）

（教师在讲解过程中能注意知识的回顾、渗透以及数形结合的思想方法，并在强化学生记忆的同时也为后续教学作好铺垫）

变式3：过点B作直线与x、y轴的正半轴分别相交于M、N两点，当△OMN面积最小时该直线方程如何？此时△OMN面积的最小值又是多少？

解：（1）如果k不存在，此时所求直线方程为x=3，但这与条件是不吻合的.

（2）如果k存在，设直线的斜率是k，此时直线方程是：y=k（x-3）+4，由题意可知k＜0.

令x=0得y=4-3k，

此时直线方程是4x+3y-24=0.

设计意图：教师在运用斜率解题的教学中一定要让学生意识到讨论斜率是否存在十分重要，本题中k＜0的分析要结合图形进行，这一过程能够引导学生感悟挖掘题中隐含信息对正确解题的重要价值.教师在直线方程得出之后又引导学生对M、N两点的坐标和B点坐标之间的关系展开进一步的研究和讨论，并引导学生大胆表达自己的想法与思路，本题多种解法也使学生对待定系数法与代数法在这一几何问题的解决中的运用过程与思想形成了清晰的认识和体会.

变式4（拓展）：过点B（3，4）作直线与x轴正半轴相交于R点，与直线y=4x于第一象限相交于S点，当△ORS的面积最小时该直线方程如何？

设计意图：学生在变式3的探究与讨论中很容易发现当△OMN面积最小时，点B正好是M、N的中点，教师此时提出了下列问题来启发学生进一步思考：这会不会是一种巧合呢？如果不是巧合，那么我们又能得到哪些结论？随后，教师安排学生在课下围绕这些问题进行分组讨论.事实上，学生在变式的研究与讨论中也确实更好地感受到了质不变而形变的哲学思想，一题多解的探究更好地锻炼了学生的解题思维，思维发散、拓展的过程使学生感受到数学知识、方法之间的内在联系，学生在不断的观察、思考与分析中也对问题背后所隐藏的真相形成了更加清晰的认知与理解，数学学习的奇妙与美好也在这一过程中展现得淋漓尽致.

三、总结思考，提升能力

最后教师引导学生一起交流学习中的体会、感受与收获，并围绕本课教学重点进行总结.

1.知识点：本课知识点包含各种形式的直线方程、方程的应用以及求直线方程的方法、求直线方程的方法包含待定系数法以及确定两个独立条件后再求解.

2.思想方法：本课基于基础原题及其变式所进行的复习教学涉及到了分类讨论、数形结合、方程等多种思想方法的运用.

四、分层作业，巩固拓展

1.面向全体学生布置的作业：（1）《导学》P13、P15-16、P18-19；（2）练习册P14-3、8；

2.选做作业：结合本课研究内容自主设计一道练习题并完成.

点评：从本节课的观摩与课后的交流中，我们不难看出，切口小、视角新是本课教学设计最为显著的特征.切口小这一特征主要表现在所提的问题围绕教学重点所设计，直线方程的求解方法以及过程中所涉及的数形结合、分类讨论、化归、方程等思想方法是本课复习教学的重点.视角新这一特征主要表现在从新的问题角度来实现旧知识的串联，并依此对学生知识的生长点进行了有意义的构建.原有知识内容的归纳和整理在切口小、视角新的设计理念中得到了很好的展现.不仅如此，本节复习课教学在教师的精心设计与引导下实现了知识的再创造，这与华罗庚教授所提倡的换角度进行复习教学的理念是完全吻合的，学生在已学知识的复习中也获得了新的感受与体验，很多无效、无趣的教学也得到了很好的规避，多角度思考问题所进行的教学对学生也产生了潜移默化的影响，我们经常提及的高层次复习在本课的教学中得以有效达成.

总之，教师在高中数学复习课的教学中应善于创设或引导学生自主创设能够理解的学习过程，仍将学习定位在教师传授、学生接受这一层面的行为早就与当今教育理念相悖了，教师在教学中应基于学生已有知识与经验进行课的设计与落实，引导学生在学习中形成自主构建知识的意识与习惯.概念教学中引领学生自主探究概念的形成；解题教学中引领学生对从无到有的思维与知识综合应用进行自主体验、感悟并掌握方法，使学生在充分体验数学思考、创新魅力与乐趣的过程中真正成为学习的主人，学生分析、解决问题的能力以及创新能力才能真正得到有意义的锻炼与提升，学生在不断掌握“三基”基础上才能在复习教学活动中获得更多的感悟与收获.