基于核心素养下信息技术妙融合的数学教学*
2018-07-23江西省赣州中学谢小翔
☉江西省赣州中学 谢小翔
当今社会,信息技术、网络技术高速发展,计算机、计算器、手机、全球互联网等逐步推广与普及,计算机、计算器、手机等的应用已经超越了解决生活、学习问题的范围,它能给予人们科学、现代的洞察力,由此导致对数学课堂教学提出了更新、更高的要求.同时,数学核心素养又是数学课程目标的集中体现,它是在数学学习的过程中逐步形成的.数据分析是数学核心素养中关键的一点,同时也是研究随机现象的重要数学技术,是大数据时代数学应用的主要方法,也是“互联网+”等现代科技领域的主要数学方法,它已经深入到科学、技术、工程、现代社会生活以及学习的方方面面.而统计中的数据较为繁杂,课堂处理起来非常不方便,结合计算器、计算机等工具来处理,往往可以达到非常不错的效益.下面结合统计中的数据分析与处理来进行融合与应用.
一、计算器处理线性回归问题
在日常生活中,由于对数据的整理和统计分析比较多,如果单独地进行人工计算与分析,显得比较麻烦,在此可以借助计算器来分析与处理数据,并进行统计与分析.特别,在线性回归计算中,求解线性回归方程,由于计算回归系数a和b比较复杂,而且数据比较多,借助计算器来完成就方便简单得多.
利用计算器求回归系数a和b的方法和步骤如下:
(1)选择计算模式:按 MODE31键,选择“回归计算”模式,类型为“线性”;
(2)输入数据:按 数据x1,数据y1DT,可输入一对数据(x1,y1),仿此输入其他几组相应的全部数据;
例1 以下表格中给出的是某地搜集到的二手房屋的销售价格y(单位:万元)和对应房屋的面积x(单位:m2)的数据信息:

二手房屋面积x(m2) 115 110 80 135 105总销售价格y(万元) 24.8 21.6 18.4 29.2 22
(1)画出以上数据对应的散点图;
(2)试根据上述数据探讨y与x之间的关系;
(3)据(2)的结果估计当房屋面积为150m2时的销售价格.
分析:根据最小二乘法的思想和公式,利用计算器,求出对应的回归系数,代入回归直线方程即可得之.再根据回归直线方程可以作一些相应的判断.
今天,他像张仲平一样兴奋,实际上,胜利大厦的业务一直是他在跟,如果一切顺利,这单业务做下来,公司可以赚五六百万,至于他的提成,公司有规定,他知道张仲平不会亏待他。当然,这里的前提是一切顺利,万一……只要一想到万一,徐艺便多少有点紧张。他在感到紧张的时候,总是忍不住要看看他女朋友的照片,好像能够以此获得某种力量。噢,准确地说,到今天为止,那还不是他真正的女朋友,只是他的暗恋对象,他一直想找个机会向她表白。这单生意做成了,也许就能让他下定决心。
解析:(1)数据对应的散点图如图1所示:

图1
(2)运用计算器计算回归直线方程yˆ=bx+a中的系数:
①按 MODE31键,选择“回归计算”模式,类型为“线性”;
②按 115,24.8DT可输入一对数据(115,24.8),仿此输入其他4组相应数据;
③按 SHIFTS-VAR▸ ▸ 1=键可得回归截距a≈1.8166;按 SHIFTS-VAR▸ ▸ 2=键可得回归系数b≈0.1962.
故y与x之间的线性回归方程为yˆ=0.1962x+1.8166.
(3)据(2),当x=150m2时,销售价格的估计值为:
yˆ=0.1962×150+1.8166=31.2466(万元).
点评:结合所画出的数据对应的散点图,可以从图像上直观判断x与y呈正线性相关,再通过计算回归系数a和b,得以求解线性回归方程.从而在此基础上对一些相关问题可以作出一个大致的判断或估计.
二、计算机处理线性回归问题
随着计算机的不断普及,在数学课堂中也可以借助计算机来处理一些相关问题.特别,对于变量之间大量数据的分析与处理,要作出相应的散点图,有时可能还要画出回归直线方程,如果采用手工方法,可能要浪费大量的时间,效果可能也不怎么样.通过计算机,这里结合Excel程序来处理有关数据的散点图和回归直线问题,显得方便快捷.
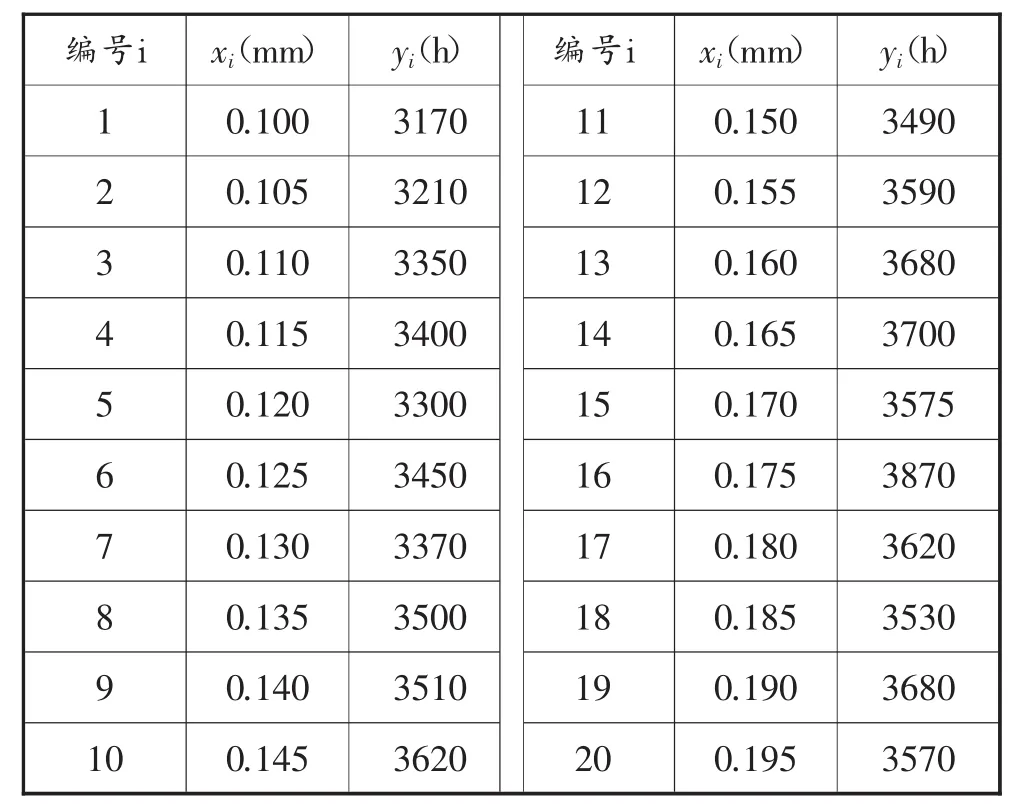
例2 某灯泡生产厂家为了提高灯泡的使用寿命,研究灯丝的粗细x(mm)与灯泡的使用寿命y(小时)之间的关系,得到如下检测数据:
编号ixi(mm)yi(h)编号ixi(mm)yi(h)1 0.100 3170 11 0.150 3490 2 0.105 3210 12 0.155 3590 3 0.110 3350 13 0.160 3680 4 0.115 3400 14 0.165 3700 5 0.120 3300 15 0.170 3575 6 0.125 3450 16 0.175 3870 7 0.130 3370 17 0.180 3620 8 0.135 3500 18 0.185 3530 9 0.140 3510 19 0.190 3680 10 0.145 3620 20 0.195 3570
利用计算机,分析题中灯丝的粗细x(mm)与灯泡的使用寿命y(小时)这两组数据的所有统计特征,并画出它们之间关系的散点图及回归直线方程.
分析:综合利用计算机来处理数据的特征及作出其相应的散点图和回归直线方程.
解析:(1)计算特征量.
在选定区域内输入原始数据,并在选定单元格内输入相应公式即可.
最大值=MAX(),最小值=MIN(),极差=MAX()-MIN(),中位数=MEDIAN(),众数=MODE(),平均值=AVERAGE(),标准差=STDEV().其中()内填写数据所在区域(图中为A1:J5)(见图2).

图2
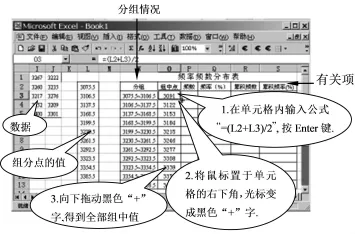
图3
(2)制作频数频率分布表.
分别在选定区域内输入表格标题、项目名称和分点值后,按下列步骤进行.
①计算组分点的值(图3).
②计算频数.选定区域P3:P13,输入公式“=FREQUENCY (A1:J5,L3:L13)”,同时按下Ctrl、Shift、Enter三个键,即可得频数(图4).

图4
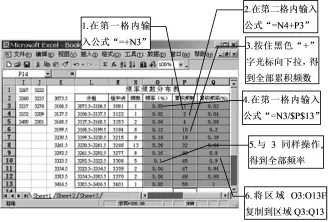
图5
③计算累积频数、频率和累积频率(图5).
(3)制作频率分布直方图、折线图和累积频数折线图.
①点击菜单“插入”“图表”,即可打开制表向导,在“图表向导-4步骤1-图表类型”中,图表类型选择“柱形图”,在子图表类型中选择第一种类型,单击下一步(图6).
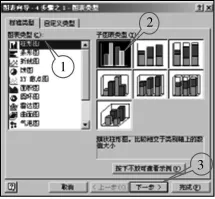
图6

图7
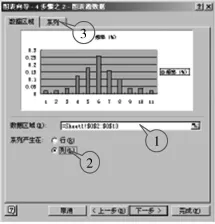
图8
②“图表向导-4步骤2-图表源数据”中,在数据区域文本框内填入存放频率数据的单元格范围“=Sheet1!$O$2:$O$13”,在“系列产生在”按钮中选“列”,单击系列(图7);在“分类(X)轴标志”文本框中填入存放组中点数据的单元格范围“=Sheet1!$M$3:$M$13”,单击下一步(图8).
③“图表向导-4步骤3-图表选项”中,根据需要在各选项卡中填写相关内容或作相应选择,单击下一步(图9).
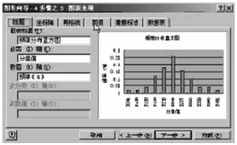
图9
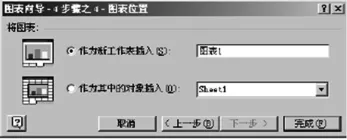
图10
④“图表向导-4步骤4-图表位置”中,作出选择后,单击“完成”(图10),即可得到直方图(图11).如果你对图表不满意,还可以利用图形工具中的其他功能进行调整.
频率分布折线图的绘制步骤与直方图相同,只需将“图表向导-4步骤1-图表类型”中的图表类型改选为“折线图”即可;而累积频数折线图的绘制只需将“图表向导-4步骤2-图表源数据”中填入的存放频率数据的单元格范围改为存放累积频率数据的单元格范围即可.
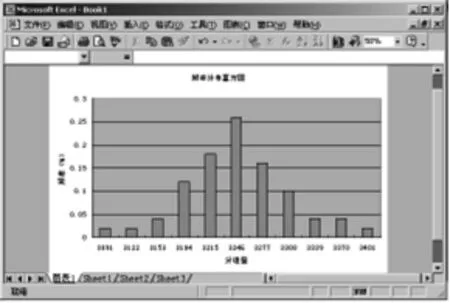
图11
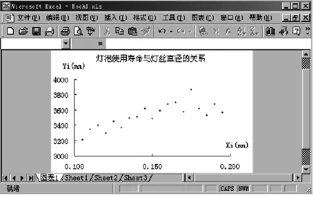
图12
(4)作散点图和回归直线.
①散点图的绘制步骤与直方图相同,只需将“图表向导-4步骤1-图表类型”中的图表类型选择改为“散点图”即可,所得散点图如图12所示.
②用鼠标右击任意一个散点,在出现的菜单中单击“添加趋势线”,出现对话框(图13);在类型中选择“线性”,单击“确定”,得到回归直线(图14).
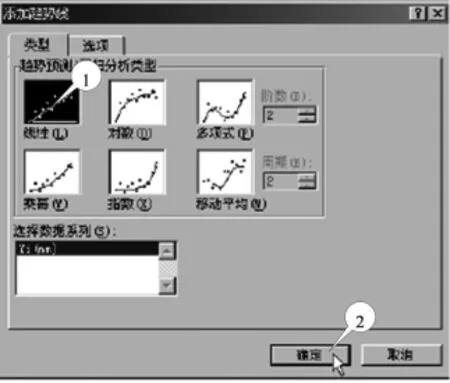
图13

图14
点评:利用计算机程序可以处理统计数据以及所有的相关知识点,这些问题结合计算机程序都可以实现.
其实,如何使数学教学适应时代的发展要求这一问题,已经成为众多数学家、数学教育家与数学教师等各方面人士所关注的焦点.数学核心素养是具有数学基本特征的、适应个人终身发展和社会发展需要的人的思维品质与关键能力.H
