基于简化模型的多层非加劲钢板剪力墙滞回性能分析
2018-07-23孙国华
王 云,孙国华
(苏州科技大学 江苏省结构重点实验室,江苏 苏州 215011)
非加劲钢板剪力墙(Unstiffened Steel Plate Shear Wall)作为一种新型抗侧力体系,在实际工程中应用越来越广泛[2]。我国中厚钢板剪力墙工程应用较多,而欧美等国家则建议使用薄钢板剪力墙。通常情况下,根据墙板高厚比可分为三类[3]:薄板剪力墙(λ>300)、中厚板剪力墙(100<λ≤300)、厚板剪力墙(λ≤100)。目前,有限元分析手段已被广泛应用于钢板剪力墙的设计与模拟方面,已有研究成果表明采用实体单元或壳单元可精确模拟钢板剪力墙的力学性能[4-5],但多高层钢板剪力墙结构采用实体单元或壳单元模拟分析时,存在单元数量巨大、操作复杂,且分析不易收敛等问题,不易实现。因此,开展非加劲钢板剪力墙结构简化分析模型的研究对其工程应用具有重要意义。
国内外学者已针对非加劲钢板剪力墙提出了一些简化分析模型。Thorburn等[6]较早地提出了钢板剪力墙的拉杆模型(SM模型),建议至少采用10根拉杆模拟。大量分析结果表明该拉杆模型可充分模拟薄钢板墙捏缩的滞回特征[7-9]。但采用拉杆模型分析中厚钢板剪力墙时,水平承载力及抗侧刚度误差较大。Rezai等[10-11]提出了板带数量更少、操作方便的多角度宏观板带模型(MAM模型)。与试验结果相比,MAM模型高估了剪力墙板的初始抗侧刚度,低估了剪力墙板的屈服承载力。当钢板剪力墙发生屈曲后,主压应力场随着剪力墙板高厚比的降低而增大,传统SM模型仅适用于主压应力可忽略的薄钢板剪力墙。为反映主压应力场的贡献,Driver等[12-13]在原有SM简化模型的基础上增加一根压杆,提出了修正的拉杆模型(Modified Strip Model,简称MSM)。MSM模型在一定程度上弥补了SM模型低估钢板剪力墙结构初始抗侧刚度及水平承载力的不足,但仅适用于钢板剪力墙在单向荷载作用下的受力分析,无法模拟钢板剪力墙的滞回性能,也不适用于动力弹塑性时程分析。In-Rak Cho&Hong-Gun Park[14]提出了一种具有复杂滞回路径且考虑受压影响的拉杆应力-应变关系曲线,将其应用于传统SM模型中,并对已完成的相关钢板剪力墙试验试件进行了数值分析,证明了所提出的简化分析模型在模拟薄板剪力墙结构时具有较高精度。周明等[15-17]提出了一种可用于模拟厚板、中厚板及薄板滞回性能的统一等代模型(Unified Strip Model,简称USM)。USM模型综合考虑了剪切作用与拉力场作用的影响,解决了传统SM模型模拟中厚剪力墙板滞回性能的不足,但略显复杂,且剪切比例系数由回归确定。郭兰慧等[18-19]提出了混合杆系模型,对于高厚比在300~600之间的薄钢板剪力墙可采用“混合2-8”模型模拟,对于高厚比在100~300之间的钢板剪力墙建议采用“混合3-7”模型模拟。混合杆系模型的拉压杆与只拉杆数量比例并不连续,有待于进一步完善。田炜烽等[20-22]提出一种可考虑对边柱不利影响的三拉杆模型(Three Strip Model,简称TSM),并同试验及精细有限元模型进行对比,验证了TSM模型分析非加劲薄钢板剪力墙的精度。
非加劲钢板剪力墙由于水平力作用导致剪切屈曲,致使存在主拉应力与主压应力场。针对薄钢板剪力墙,采用忽略主压应力场的简化模型分析其滞回性能时,误差较小。对于中厚钢板剪力墙,一旦忽略主压应力的贡献,则误差较大。文献[1]在传统SM板带模型的基础上,将原只拉板带改为拉压板带,从板带的恢复力模型上反映了钢板剪力墙主压应力的贡献,提出了一种可用于分析薄板、中厚板及厚板剪力墙的统一简化滞回分析模型(Unified Hysteresis Strip Model,简称UHSM模型),进一步完善了非加劲钢板剪力墙结构滞回性能的数值模拟,文章对多层非加劲钢板剪力墙采用UHSM模型的分析精度进行了验证。
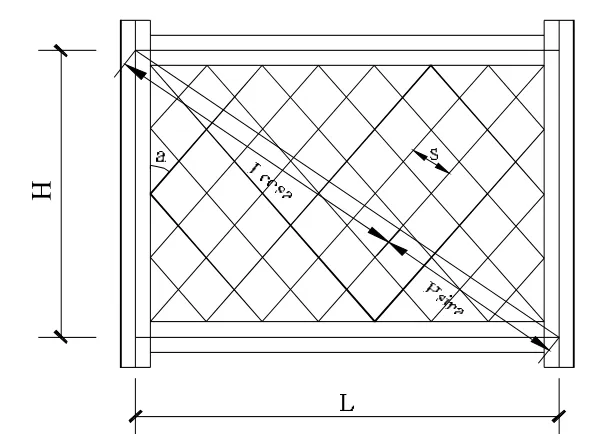
图1 钢板剪力墙的几何模型
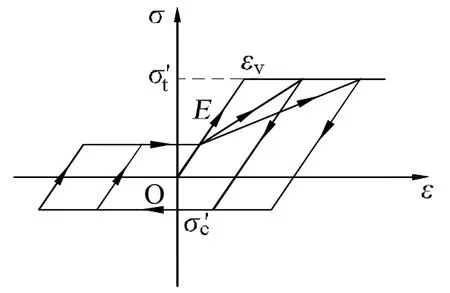
图2 UHSM模型中板带的恢复力模型
1 非加劲钢板剪力墙的简化滞回分析模型
文献[1]所提出的UHSM简化滞回分析模型是对传统SM模型的一种修正,将传统SM模型的拉杆赋予了新的滞回准则,其几何模型仍与传统SM模型一致(见图1)。根据非加劲钢板剪力墙的滞回特征,将剪切屈曲后的剪力墙板分为主拉应力场(拉力场)和主压应力场(剪切作用),在板带的恢复力模型中包含主压应力场的贡献(见图2)。其中,σ'c为主压应力;σ't为主拉应力。 可分别按公式(1)、(2)计算。

式中,τcr为剪力墙板的临界弹性屈曲应力;θ为主拉应力与水平向的夹角;fy为钢材的屈服强度。
2 多层非加劲钢板剪力墙的算例设计
2.1 设计概况
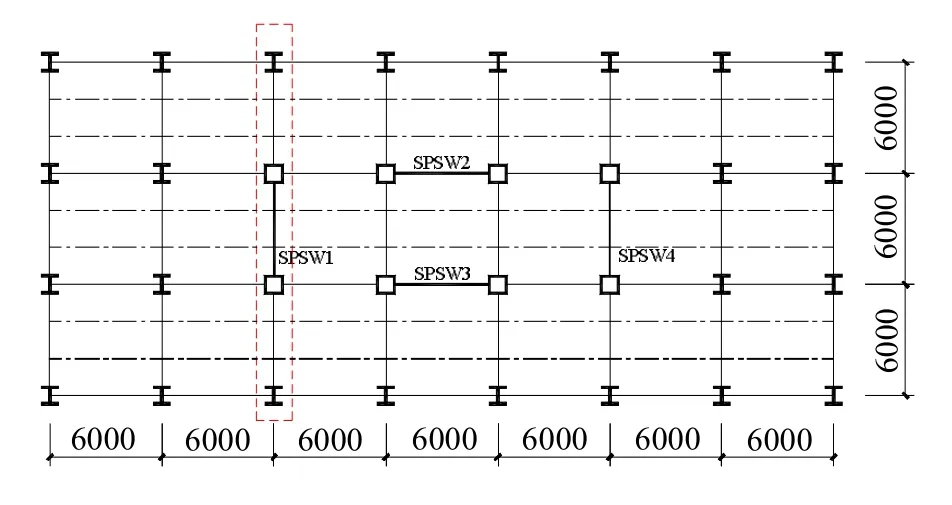
图3 三层钢板剪力墙算例的平面布置
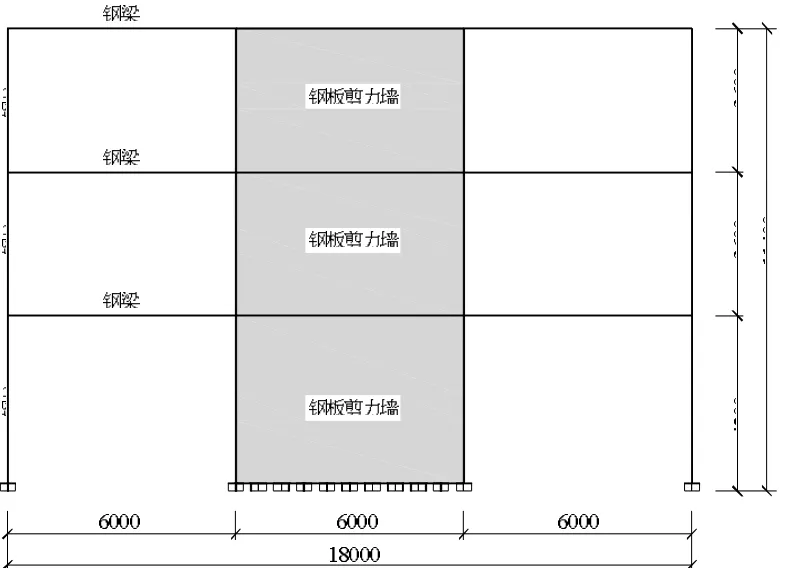
图4 三层钢板剪力墙算例的立面布置
所设计的3层钢板剪力墙算例位于8度抗震设防区,设计地震基本加速度为0.2g,二类场地,设计地震分组为第一组。结构平面布置见图3。该结构布置了2榀横向钢板剪力墙结构,设计时假定每榀钢板剪力墙结构承担一半的水平地震力。结构底层层高为4.2 m,二、三层层高为3.6 m,跨度为6 m。梁柱节点采用刚性连接。剪力墙板采用Q235B钢材,框架梁、柱及其他构件均采用Q345B钢材。竖向荷载根据《建筑结构荷载规范》[23]和建筑构造普通做法取值,现浇钢筋混凝土楼板厚120 mm,混凝土等级为C20。标准层楼面恒载为4.56 kN/m2,顶层恒载为 4.85 kN/m2,活载均为 2.0 kN/m2;标准层外梁承受外墙均布荷载为 10.3 kN/m,顶层外梁承受女儿墙均布荷载为3.15 kN/m。结构的立面布置见图4。
2.2 截面设计
通过迭代设计,最终确定出3层3跨钢板剪力墙算例基底设计剪力为1 256.9 kN。表1为3层3跨钢板剪力墙算例的截面。其中,带墙跨钢柱采用箱形截面,其余框架梁、柱均采用H形截面。

表1 3层3跨钢板剪力墙算例的构件截面 mm
3 多层非加劲钢板剪力墙有限元模型的建立
由于本次分析中钢板剪力墙采用了微观有限元模型,为减少单元数量,忽略了边跨的影响。在表1所设计的算例基础上,考虑钢板剪力墙高厚比的影响,设计了2个单跨3层钢板剪力墙算例,见表2。其中,钢柱、钢梁截面仍按表1确定。

表2 3层钢板剪力墙算例的基本信息
3.1 微观有限元模型的建立
3.1.1 多层钢板剪力墙算例的有限元模型
3层单跨钢板剪力墙算例的几何尺寸见图5(a),试件的有限元模型见图5(b)。钢柱、钢梁、剪力墙板均采用SR4壳单元模拟,单元网格类型为structure,网格尺寸为50 mm×50 mm,梁柱与墙板采用merge方式连接为整体,柱、墙板均与基底固接。通过引入各层剪力墙板的1阶屈曲模态作为初始缺陷,并采用ABAQUS/Explicit动力显示模块进行滞回分析。其中梁柱钢材均采用双线性本构模型,见图6。采用Mises屈服准则,通过随动强化模型反映钢材的包辛格效应。钢材的弹性模量为E=2.06×105N/mm2,泊松比ν=0.3。
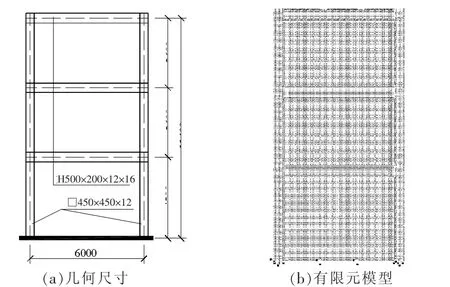
图5 试件的几何尺寸及有限元模型

图6 钢材的本构模型
3.1.2 加载制度
通常情况下,加载制度的选择主要取决于研究目的,不同的加载制度会得到不同结果。为更全面地对比钢板剪力墙采用宏观简化滞回分析模型的模拟精度,共采用了四种加载制度进行验证。其中,第1种为标准滞回加载制度,见图7(a);第2种采用考虑近场速度脉冲影响近场加载制度,见图7(b);第3种采用等目标位移循环(位移延性系数μ=2)的加载制度,见图7(c);第4种采用等目标位移循环(位移延性系数μ=4)的加载制度,见图 7(d)。
第三、四种加载制度中涉及钢板剪力墙结构的位移延性系数,目标位移延性系数通常定义为结构整体目标位移与屈服位移之比,即μ=Δt/Δy。式中,Δt、Δy分别表示钢板剪力墙结构整体的目标位移与屈服位移。因此,需要先确定钢板剪力墙结构的显著屈服位移,采用FEMA-273方法确定钢板剪力墙结构的屈服位移(见图8)。基于FEMA-273方法确定出试件TS1、TS2的屈服位移,见表3。
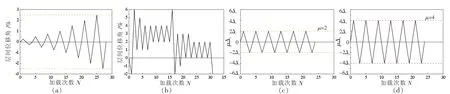
图7 加载制度
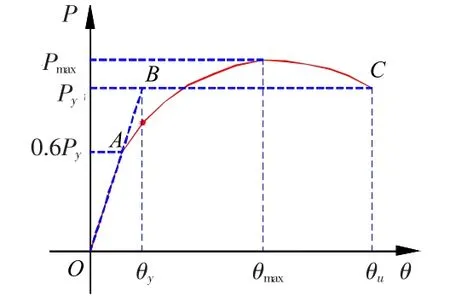
图8 FEMA-273方法确定的显著屈服点
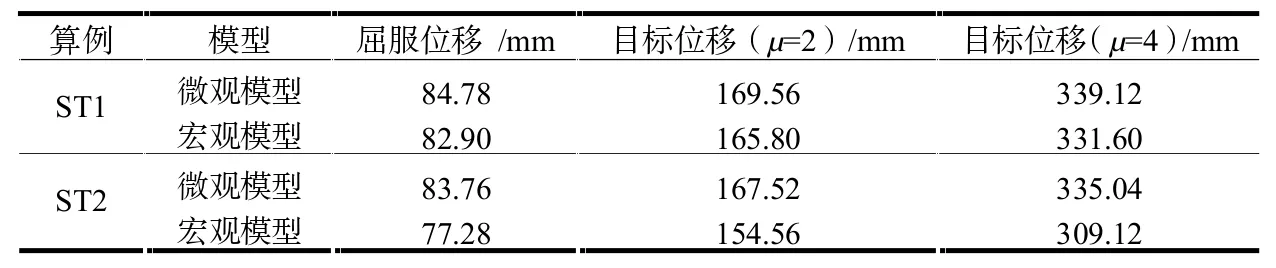
表 3 宏观模型与简化模型屈服位移及μ=2、4的极限位移
3.2 宏观有限元模型的建立
图9为3层单跨钢板剪力墙算例的宏观有限元模型。其中,剪力墙板的板带数量取为10,倾角为θ,面积为As。宏观有限元模型中周边的钢柱、钢梁均采用双线性应力-应变关系曲线,板带的恢复力模型中参数按文献[1]提出的UHSM模型确定,见表4。梁柱及简化板带均采用纤维单元。梁柱采用刚接,板带与梁柱采用铰接,柱、板带与基底采用固接,加载制度与微观精细有限元模型一致。
图9 宏观模型有限元模型
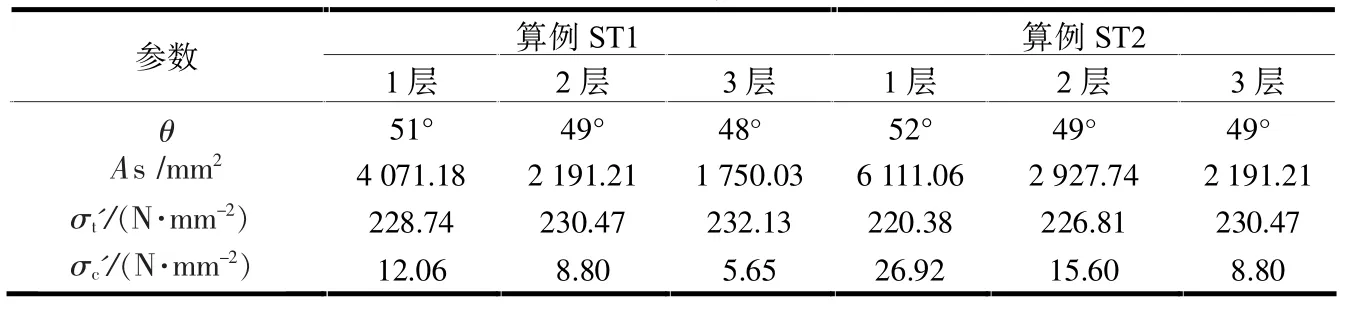
表4 3层钢板剪力墙算例宏观简化滞回分析模型中板带的主要参数
4 有限元模拟结果与分析
4.1 滞回曲线
图10分别给出了3层钢板剪力墙算例ST1、ST2在四种加载制度下宏观简化滞回分析模型与微观有限元模型分析获得的水平荷载-顶点位移角(P-δ)的滞回曲线。
由图10可知,在标准加载制度作用下(图10(a)、(b)),算例ST1、ST2由宏观简化滞回分析模型得出的滞回曲线与微观模型分析结果吻合较好,可反映钢板剪力墙的捏缩特征。随着剪力墙板高厚比的增大,算例ST1的滞回曲线较算例ST2更为捏缩。由于钢板剪力墙的宏观简化滞回分析模型中周边钢柱、钢梁采用纤维模型来模拟,未能充分反映梁柱的抗剪贡献,故其计算的水平承载力略低于微观模型。在近场加载制度作用下(图10(c)、(d)),算例ST1、ST2采用两种模型模拟的滞回曲线拟合较好,速度脉冲导致了钢板剪力墙算例突然出现较大塑性变形,该加载制度主要用于评估速度脉冲对结构性能的影响。其中采用宏观简化滞回分析模型模拟最大水平承载力略低于微观模型结果,但从整体对比来看,两者误差较小。采用μ=2的等位移循环加载制度时(图10(e)、(f)),算例ST1、ST2采用两种模型模拟的滞回曲线拟合较好。在首次正向加载过程中,由宏观简化滞回分析模型模拟的初始刚度略低于微观模型,最大水平承载力亦略低。其中,算例ST1低估约6%,算例ST2低估约11%。在等位移加载制度作用下,宏观简化滞回分析模型模拟的滞回曲线略饱满于微观有限元模型分析结果,且在等目标位移循环时的最大水平承载力退化较为缓慢。采用μ=4的等位移循环加载制度时(图10(g)、(h)),算例ST1、ST2采用两种模型模拟的滞回曲线拟合较好。随着所施加的目标位移增大,结构的弹塑性变形得到充分发展,当结构达到最大目标延性时,采用宏观简化滞回分析模型分析水平承载力仍低于微观模型结果。其中,算例ST1低估约10%,算例ST2低估约11%。
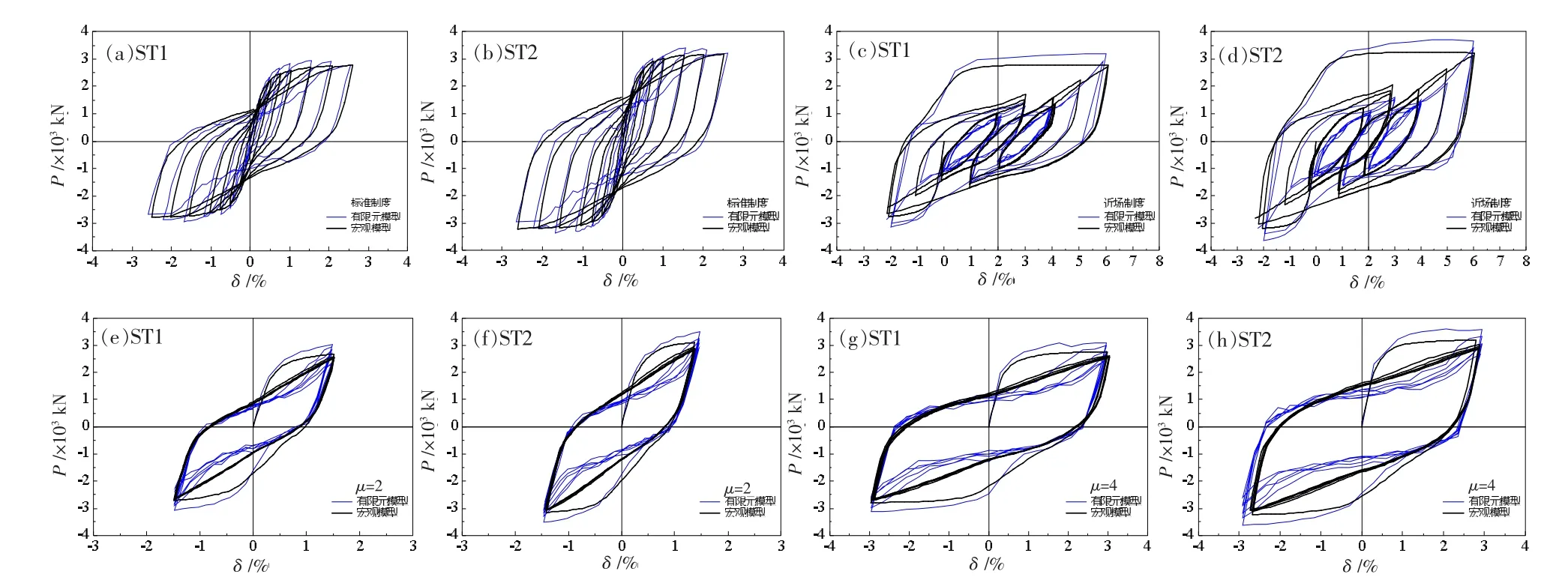
图 10 算例ST1、ST2在四种加载制度作用下的滞回曲线对比
4.2 骨架曲线
图11 给出了3层钢板剪力墙算例ST1、ST2在第1种标准加载制度及单向加载作用下宏观简化滞回分析模型与微观有限元模型分析获得的水平荷载P-顶点位移角δ的骨架曲线。
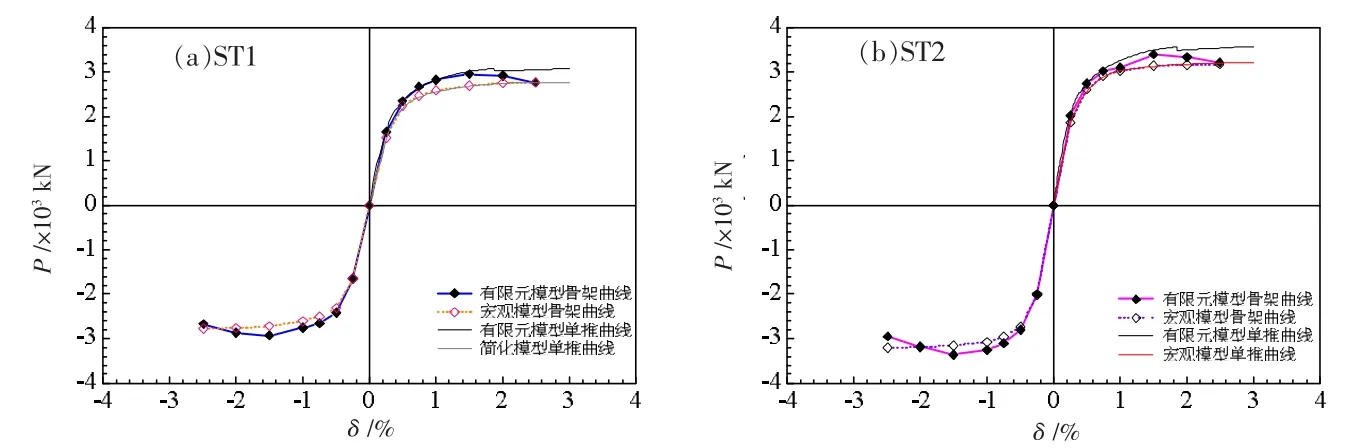
图11 算例在标准加载及单向加载作用下宏观模型与微观模型骨架曲线对比
由图11可知,采用宏观简化滞回分析模型模拟的算例ST1、ST2的骨架曲线与微观模型分析的骨架曲线均呈“S”形状,两者吻合较好。其中,采用宏观简化滞回分析模型在标准加载作用下的曲线与单向加载获得的骨架曲线基本重合,且后期趋势一致。采用微观精细模型模拟的标准加载制度作用下的骨架曲线在加载后期存在下降段,而微观精细模型模拟的单向加载曲线无下降段,这与单向加载作用下的曲线存在误差。总体上,在顶点位移角达到2%时,算例ST1、ST1基于两类模型在单向加载及标准加载下的水平承载力误差均在10%以内,能满足工程设计要求。
4.3 抗侧刚度
图12给出了算例ST1、ST2分别在标准加载制度及μ=2、4加载制度下,采用宏观简化滞回模型与微观有限元模型分析获得整体抗侧刚度退化曲线。图中,K为割线刚度,δ为顶点位移角。
由图12(a)、(b)可知,在标准加载制度下,两种模型模拟的抗侧刚度曲线几乎重合。在弹性阶段,结构抗侧刚度退化迅速;进入弹塑性阶段,结构抗侧刚度退化趋于平缓。其中,算例ST1、ST2采用宏观简化滞回分析模型模拟的初始抗侧刚度分别为53.53、65.21 kN/mm,采用微观有限元模型模拟的初始抗侧刚度分别为58.38、70.72 kN/mm,两者误差分别为 8.3%,7.8%。由图 12(c)、(d)可知,在 μ=2 的加载制度下,结构均进入弹塑性阶段,两种模型模拟的抗侧刚度曲线吻合较好。随着循环次数的增加,结构出现累积损伤,其抗侧刚度开始降低。由于高厚比越大,剪力墙板越易屈曲,故算例ST1采用微观有限元模型模拟的抗侧刚度退化速度明显快于宏观简化滞回分析模型模拟结果。此外,算例ST1、ST2在第1级循环下采用宏观简化滞回分析模型模拟的初始抗侧刚度分别为15.76、19.73 kN/mm,采用微观有限元模型模拟的初始抗侧刚度分别为18.02、21.07 kN/mm,两者误差分别为 12.5%、6.4%。 由图 12(e)、(f)可知,在 μ=4 的加载制度下,两种模型模拟的抗侧刚度曲线拟合较好。由于目标位移增大,钢板剪力墙结构均进入了更深的弹塑性阶段,初始抗侧刚度降低,退化趋于平缓。其中,算例ST1、ST2在第1级循环下采用宏观简化滞回分析模型模拟的初始抗侧刚度分别为 8.21、10.35 kN/mm,采用微观有限元模型模拟的初始抗侧刚度分别为 9.20、10.81 kN/mm,两者误差分别为11%、4.3%,略小于μ=2加载制度作用下的计算结果。

图12 不同加载制度作用下两种模型的抗侧刚度曲线对比
4.4 滞回耗能
图13分别给出了算例ST1、ST2在4种加载制度作用下,采用宏观简化滞回模型与微观有限元模型分析获得累积滞回耗能对比。图中,Etotal为累积滞回耗能。由图13可知,虽然宏观简化滞回分析模型可以较好地模拟非加劲钢板剪力墙结构的滞回性能,但所计算的累积滞回耗能同微观精细有限元模型相比仍存在差异,误差在9%~19%之间。这主要是因为采用简化滞回分析模型模拟的非加劲钢板剪力墙结构的滞回曲线仍略显饱满所致。
图14分别给出了算例ST1、ST2在第1种标准加载制度作用下,采用宏观简化滞回模型与微观有限元模型分析获得等效黏滞阻尼比(ξeq)的对比曲线。其中,δ为顶点位移角。由图14可知,算例ST1、ST2的等效黏滞阻尼比曲线拟合较好,均随着结构进入塑性深度增加呈显著的增大趋势。其中采用宏观简化滞回分析模型模拟的等效黏滞阻比略大于微观有限元模型模拟结果,进一步说明采用宏观简化滞回分析模型模拟的钢板剪力墙结构的滞回曲线比微观有限元模型模拟结果略显饱满。
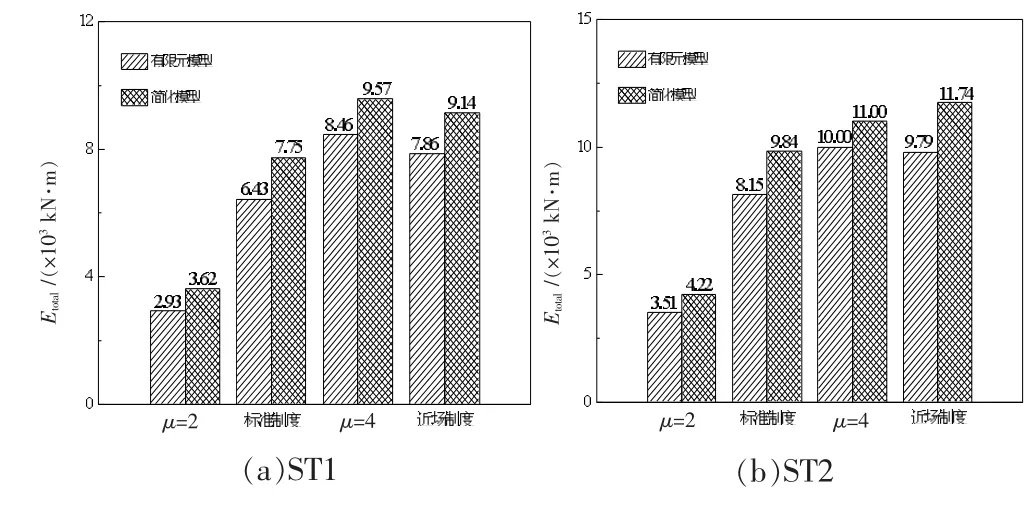
图13 4种加载制度作用下两种模型的累积滞回耗能对比
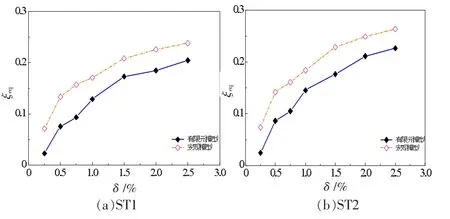
图14 标准加载制度作用下两种模型等效黏滞阻尼比的对比
5 结论
通过对比非加劲钢板剪力墙结构采用宏观简化滞回分析模型与微观有限元模型在四种不同加载制度作用下所获得滞回曲线、骨架曲线、刚度退化曲线及滞回耗能,主要得出以下结论:
(1)统一简化滞回分析模型在对考虑不同加载制度下非加劲钢板剪力墙滞回性能模拟方面具有良好的精度。
(2)统一简化滞回分析模型可精确评估非加劲钢板剪力墙结构在不同加载制度下的水平承载力。
(3)统一简化滞回分析模型能较好评估非加劲钢板剪力墙结构抗侧刚度的退化情况。当采用标准加载制度时,在顶点位移角达到1%之前,算例的抗侧刚度退化迅速;在顶点位移角达到1%之后,钢板剪力墙充分进入弹塑性阶段,其抗侧刚度退化趋于均匀缓慢。当采用等位移循环加载制度时,两类模型的抗侧刚度退化曲线相对平稳。
(4)统一简化滞回分析模型可较好地评估非加劲钢板剪力墙的累积滞回耗能。总体上,非加劲钢板剪力墙结构基于宏观简化滞回分析模型获得的累积滞回耗能略大于采用精细有限元模型分析结果。
