并行化非结构重叠网格隐式装配技术

常兴华，马戎，张来平1,

1. 中国空气动力研究与发展中心 空气动力学国家重点实验室，绵阳 621000 2. 中国空气动力研究与发展中心 计算空气动力学研究所， 绵阳 621000

重叠网格技术最早用于解决复杂构型的结构网格生成难题[1]，后来逐渐推广应用于非结构网格以及运动边界问题。目前已经成为处理运动边界问题的有效方法之一，在多体分离、旋翼等问题中应用广泛[2]，并已经形成了一系列有代表性的软件[3]。

网格装配是重叠网格的核心流程，其目的是将网格中不参与计算的网格点(单元)删除掉(称为“挖洞”过程)，并且确定出重叠区域内单元的插值关系。常见的重叠网格装配过程是将挖洞过程与确定插值关系的过程分开处理。在挖洞过程中，需要根据挖洞曲面判断点(单元)是否在曲面内部，常见的判断方法有矢量判别法[4]、射线求交法[5]、洞映射方法[6]、目标X射线法[7]等。在确定初始的洞边界之后，一般还要采取一些优化措施如割补法[8-9]对洞边界进行优化，使其远离壁面。“挖洞”结束之后，再通过查询算法确定出插值点(单元)的贡献单元。

理论上非结构重叠网格可以沿用结构网格上成熟的网格装配技术，且由于非结构网格更加适用于复杂构型，在处理复杂构型时不需要像结构网格那样生成很多的网格块，因此相比结构网格自动化程度更高。Nakahashi等[10]最早开展了非结构重叠网格相关的研究工作，他们通过查询节点的宿主单元并通过对比其壁面距离判断节点的属性(简称“壁面距离准则”)，其实质上是一种“隐式”挖洞方法(Implict Hole-Cutting, IHC，其概念之后由Lee和Baeder[11]在2003年提出)。Togashi等[12]进一步将该方法推广应用于复杂的多体相对运动问题，并可以处理多体分离过程中物体相交的情况。Loehner[13]、Luo[14]等在Nakahashi方法的基础上，采用单元的尺度和壁面距离的组合量作为单元属性的判断标准，使插值单元和贡献单元的大小匹配，有助于提高插值稳定性并减少插值误差。国内，田书玲[15]较早开展了非结构重叠网格技术研究，通过改进单元查询算法提高了重叠网格的装配效率，并将其应用于多体分离问题的数值模拟。

这种基于单元品质的非结构重叠网格隐式装配方法具有非常高的自动化程度，装配效果较好，但是其仍然存在如下几个瓶颈问题：

1) 非结构网格本身占用内存较大，由于在重叠网格装配过程中需要存储额外的拓扑信息，因此当网格规模增加后内存消耗量会急剧增加。

2) 查询计算量较大。尽管可以采用交替数字树(Alternation Digital Tree，ADT)数据结构[16]或者一些基于网格拓扑信息的快速查询方法，但是计算效率和显式挖洞技术相比仍然有较大差距，并且查询的计算量会随着网格规模的增加而急剧增大。

3) 由于挖洞过程是在查询和判断中自动完成的，有可能会产生一些 “孤岛”从而导致计算域不是单连通域。

随着CFD技术的不断发展，工程领域对CFD的期望也越来越高。在航空航天以及民用领域，越来越多的工程应用希望CFD能够采用更大规模的计算网格，模拟更真实的复杂外形，并能够更好地模拟分离流动、湍流流动现象。为了适应超大规模的计算网格，并行化装配是一个必然的选择。

在并行化重叠网格装配技术方面，Zhang和Owens[17]发展了并行化的非结构重叠网格自动装配技术，通过判断单元的棱线是否和壁面相交确定出洞内点，装配过程分为并行挖洞和并行查询两个过程。Sitaraman等[18]开发了并行化的非结构重叠网格隐式装配软件PUNDIT，通过将查询区域分割成均匀的六面体区域，提高了查询效率。Roget和Sitaraman[19]进一步改进了PUNDIT的装配算法，提高了其自动化程度和鲁棒性。目前PUNDIT已经在美国CREAT-AV项目[20]的Helios系统中进行了集成。Mavriplis研究团队[21]则针对非结构网格的间断-伽辽金格式，开发了适用于高阶格式的非结构重叠网格并行装配软件TIOGA。Zagaris[22]、Landmann[23]等针对结构重叠网格，亦开展了并行装配方面的研究工作。国内，梁姗等[24]发展了一种并行化且具有局部数据特性的结构网格挖洞技术，具有较好的并行计算效率。

从国内外的相关研究工作来看，并行化重叠网格装配技术研究刚起步不久，且由于重叠网格装配方法自身的多样性，其采用的并行化策略也不尽相同。然而，各种并行化重叠网格装配技术的最终目标是一致的，那就是自动化、鲁棒、高效。就隐式装配方法而言，其具有自动化程度高、装配效果好的特点，与非结构网格自身的特点非常吻合。但是其计算量较大，效率较低，从国外相关研究工作来看，相应的并行计算技术仍在不断发展完善之中，国内更是缺乏相关的研究工作。为了适应未来超大规模网格计算的需求，非常必要针对并行化的隐式装配技术开展研究。

本文针对格心型的有限体积算法，发展了一种并行化的非结构重叠网格隐式装配技术。该技术采用壁面距离准则判断点的属性，并通过物理边界推进的方法填充活跃区域，不需要进行是否在物体内部的判断，并且能够避免出现“孤岛”问题。采用网格分区的方式实现了装配技术的并行化，在每一个分区内建立单独的ADT子树用于查询，减小了内存消耗量。二维以及三维的测试算例证明了该方法的有效性，并且展示了该方法在超大规模重叠网格计算中的应用前景。

1 非结构重叠网格装配技术

本文的重叠网格技术以格心型的非结构有限体积算法为背景，装配流程如图1所示。首先将网格点的类型划分为活跃(1属性)和非活跃(0属性)，然后再根据活跃点判断出活跃单元(1属性)，最后搜索出插值单元(-1属性)并查询其贡献单元。在进行网格生成时，根据实际问题，围绕每一个物体或者部件生成独立的网格块(block)。对于嵌入在大网格内的子网格块，需要将其外边界设定为重叠边界条件。在网格装配的预处理阶段， 计算出每一个block内网格的单元体积、单元中心点、面的面积、面的法向、面的中心点等几何信息，重构出计算所需的“点-体”和“体-点”拓扑信息。之后求出所有网格点在该block内的壁面距离，并在每一个block内建立后续查询所需要的ADT数据结构。

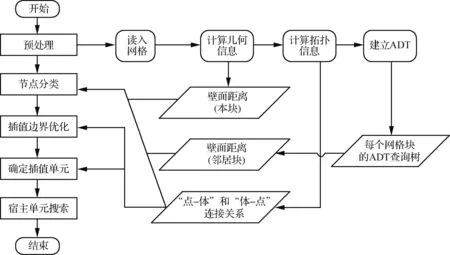
图1 非结构重叠网格装配流程Fig.1 Assembling procedure of unstructured overset grids

1.1 判断点的类型

本文采用了和文献[12]类似的基于单元(点)品质的“隐式”挖洞方法。单元的品质有多种取法，为了提高装配的效果，文献[12-13]采用壁面距离作为判断准则。文献[14]则采用了单元尺度和壁面距离的组合量。文献[15]的研究表明，以网格点的最小壁面距离作为标准，通过结合一定的洞边界优化措施，可以达到相当不错的装配效果，因此本文选择点的壁面距离作为判断标准。

在预处理阶段，已经求出了各个block内的网格点距离该block内固壁边界的距离。对于没有固壁边界的block，则直接给定一个固定的距离(这个给定的参数会影响该block内活跃区域的大小)。之后搜索网格点在邻居block内的宿主单元，并通过插值求出其在邻居block内的壁面距离。对于多个block相互重叠的情况，某网格点可能存在多个宿主单元，此时应当选择其中壁面距离的最小值。最后，根据网格点在本block内的壁面距离dist_1以及其在邻居块内的最小壁面距离dist_2确定其类型：如果dist_1大于dist_2，则该点属性为0，否则属性为1。

通过以上操作，可以确定出一部分网格点的属性，但是仍然有一些网格点由于查找不到宿主单元而无法确定其属性。这些剩余点有两种可能：一种是处于非重叠区内，其属性应当为1；另一种是处在另外一个物体内部，属性应当为0。此时文献中常用的方法是进行是否在物体内部的逻辑判断，以便进行进一步的区分。本文则采用了一种物理边界推进的方法确定这些剩余点的类型：物理边界上的点必定为活跃点，其属性设置为1，然后根据“点-体”和“体-点”的拓扑关系逐步向计算域内推进并扩大活跃点的范围，直到推进到0类型的点为止。在具体的推进过程中采用了如下的循环迭代方式：针对所有单元进行循环判断，如果单元中的一个节点为活跃点，则单元属性设置为活跃，其所有节点也设置为活跃，并立即生效且应用到下一步循环。采用这种循环方式可以将物理边界点的属性快速拓展至计算域内场，并且可以保证计算区域的单连通特性，避免了重叠网格隐式装配方法中常见的“孤岛”问题。

1.2 判断单元的类型

在判断出点的类型之后，再根据“体-点”的网格拓扑信息判断出单元类型。本文采用了如下判断准则：一个单元的所有点为活跃点(1属性)，则该单元为活跃单元(1属性)；如果该单元的所有点为非活跃点，则该单元为非活跃单元(0属性)；剩下的单元为插值单元(-1属性)。

最后搜索插值单元的宿主网格块和宿主单元。对于存在多个block相互重叠的情况，有可能会查找到多个宿主单元，此时仍然采用和1.1节中相同的做法，选取壁面距离最近的那个宿主单元建立最终的插值关系。

1.3 提高算法鲁棒性的措施

为了提高非结构重叠网格应对复杂工程问题的能力，本文采用了一些提高网格装配鲁棒性和效率的措施。

1) 对插值边界进行优化。采用非结构网格中“点-体”和“体-点”的拓扑关系拓展1～2排活跃点，适当扩大活跃区域，使得插值单元完全落在邻居zone的活跃区域内。

2) 对于嵌入在大网格内的子网格块，需要在其重叠边界上预留一排单元和一排点作为缓冲区，缓冲区内的点和单元不参与宿主单元查询。

3) 在重叠网格装配的过程中引入容差ε，其大小应当小于最小的网格点间距(如最小网格间距的1/10)。在计算单元的“最小盒子”以及判断点是否在单元内时，留一个大小为ε的裕量，以防止由于某些极端原因而查找不到宿主单元的情况(例如点正好处在某个单元的边界上，或者对于存在对称面的情况)。

4) 为了提高查询效率，采用ADT数据结构用于宿主单元查询。对于每一个网格块，以围绕每一个网格单元的最小盒子作为建立ADT树的依据。

2 基于网格分区的并行通讯策略及装配效率

基于第1节的非结构重叠网格自动装配方法，采用分区并行的策略，将每一个block分为若干个网格区(zone)，每一个进程负责一个或者若干个zone的计算。和未分区情况下的装配过程类似：对于每一个zone内的网格点，在其他所有zone内进行查询并寻找最小壁面距离，从而判断点的属性。

并行装配的核心内容是查询所有zone内网格点的所有宿主单元，根据查询方式不同有两种并行策略：第1种策略是每个进程仅对其所负责的zone内的网格点进行查询，然后进行点和单元类型的区分。这种方法比较直观，操作流程和第1节相同，易于实现。但是这种并行模式需要在本进程内存储一个全局的计算网格，并且同时需要全局网格的几何信息和拓扑信息，内存占用较大。此外，搜集这个全局计算网格的过程需要较多的数据通讯，必然会影响并行效率。特别对于运动网格的问题，每一步重构都需要对全局计算网格的信息进行通讯，会影响到整个非定常计算的效率。因此，本文采用了第2种策略：每一个进程都对所有计算点进行查询，但是只在本进程所负责的zone内查询贡献单元，最终的查询结果通过各个进程之间的并行通讯来确定。图2给出了两种并行模式的对比示意图。

对于图2(b)所示的第2种策略，其流程和图1 所示的串行情况下的流程是类似的，首先各个进程要对其所负责的zone进行预处理操作，之后再分别进行点和单元类型的判断。

图2 两种并行化的装配策略Fig.2 Two approaches for parallel assembling

在判断点的类型时，需要先搜集各个zone的网格点坐标并进行广播通讯，在每个进程内形成整体的待查询点集，然后在本进程所负责的zone内查询该点集的宿主单元并计算壁面距离。点在所有邻居zone内的最小壁面距离最终通过各个进程间的并行通讯来完成。

并行情况下同样通过物理边界推进来填充活跃区域。但由于每一个block被分解成了若干个zone，每推进一次，就需要在分区边界上进行单元属性的通讯。图3所示为分区并行情况下物理边界推进过程示意图，其仍然借助了“点-体”和“体-点”的拓扑信息，其中从点到体的过程与串行情况一致，唯一不同的是在从体到点的推进过程：分区并行情况下需要首先对分区边界面上的单元属性进行通讯，将邻居zone的单元属性储存在本zone分区边界上的虚拟单元内，之后借助分区边界面的“面-点”关系使属性顺利拓展到边界点。在插值边界优化以及判断单元属性的操作中，需要用到图3所示的通讯过程，因此将该通讯过程进行了封装，以方便程序的调用。

在查找插值单元的宿主单元过程中，采用和图2(b)类似的策略：首先搜集所有zone里面需要进行查询的插值单元，通过广播并行通讯在每个进程内形成整体的待查询单元。然后各个进程在其所负责的zone内进行查询，最后各个进程再通过并行通讯来确定其插值单元的宿主区和宿主单元。

不失一般性，假设两套规模为N(网格点和单元数)的block进行重叠装配，则在未分区串行装配的情况下，装配所需的计算量约为2N个网格点在N个单元内查询所需的时间。在采用ADT快速查询算法的前提下，装配所需计算量约为2N(log2N)(一个点在规模为N的block内的查询计算量约为log2N)。

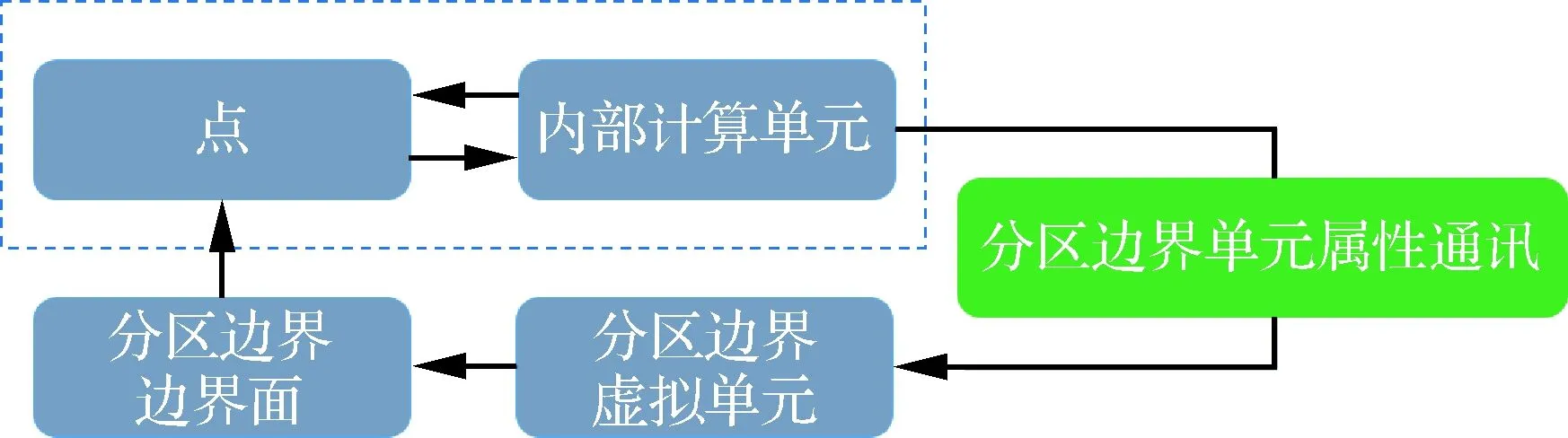
图3 分区并行情况下物理边界推进流程Fig.3 Procedure of boundary advancing in parallel environment

在本文的分区并行策略下，假设每一个block被均匀分成了M个网格区(zone)，则两套规模为N的block之间的查询转变为2M套规模为N/M的网格间的查询。显然属于同一个block的zone之间不需要进行查询，因此对于每一个zone而言，其查询计算量为Nlog2(N/M)。

在实际查询过程中，可以引入一些预判方法加速查询过程：① 计算出包围每一个zone的最小盒子，根据该盒子信息可以对两个zone是否存在重叠区域进行快速的预判断，如果两个盒子不重叠，则两个zone之间不进行查询；② 查询一个点在某zone内的宿主单元时，先判断其是否落在该最小盒子之内，否则不进行查询。加入上述预判断之后，对于某zone而言仅需要对其他一部分zone内的一部分点进行判断即可。假设网格分布均匀，分区大小均匀，在完全理想的情况下，处于非重叠区域内的zone其查询计算量为0，因为没有点落在其盒子内；而处于重叠区内的zone，大约仅需要查询N/M个点(落在其最小盒子之内的其他block的网格点数)。因此，在完全理想的情况下，单个zone查询的计算量最多为N/M(log2(N/M))，这也决定了并行情况下进行网格装配所需的时间。

在实际问题中，网格单元大小、网格分区大小、分区形状肯定不均匀。例如远场区域的计算网格尺度必然较大，此处的分区区域也较大；而靠近壁面的网格尺度较小，分区区域也较小。因此，对于某zone而言，落在其最小盒子之内的其他block的点数肯定不可能为理想状态下的N/M。假设实际情况下落在某zone的最小盒子内的点数为k(N/M)，查询的计算量变为k(N/M)log2(N/M),k∈(1,M),k和计算网格的均匀度、分区数、分区的均匀度相关，理想情况下k为最小值1。而在实际情况中，由于在计算域远场存在较大的网格分区，其最小盒子甚至有可能覆盖了其他整个block，因此k的最大值有可能为M。

所以，对于实际问题的多区并行装配，其装配时间是和分区数、网格均匀度以及分区均匀度密切相关的。为了减少针对实际问题的装配时间，最有效的办法是增加分区数，这样一方面会减少每个zone内用于查询的网格单元规模，另一方面则会显著减少其“最小盒子”的大小，减少实际进行查询的点数。

除此之外，本文还采用了另外一种加速策略：对重叠区进行预判断。首先求出覆盖每一个block的最小盒子，然后对于某一个block，判断其中的点是否落在其他的block内，如果是则标注为重叠区域点，否则标注为非重叠区域点。对于非重叠区域的点，不参与建立整体查询点集，不参与宿主单元搜索，同时在计算zone的最小盒子时也不予考虑；对于非重叠区域的单元，则不参与建立ADT。经过上述重叠/非重叠区的预判断，可以有效提高网格装配效率，原因在于：① 将远场非重叠区的zone进行了进一步细分，减少了其中的有效点，从而缩小了其“最小盒子”，也就减少了实际进入该zone内进行查询的点数；② 处于非重叠区内的点不参与整体查询点集的建立，因此减少了并行通讯量，减少了每个进程中的内存开销；③ 减少了非重叠区域内zone的有效单元数，也就减小了用于查询的ADT的规模。

在网格生成时着重考虑网格的均匀性，并通过上述这些优化措施，可以有效减少k值的大小，从而减少并行装配的计算时间。

3 非结构重叠网格装配实例

3.1 二维装配实例

图4 二维非结构重叠网格装配实例(3个圆柱)Fig.4 Example of assembling of 2D unstructured overset grids (three cylinders)

图4所示为3个二维圆柱网格的装配结果。圆柱直径为1，背景网格的壁面距离设置为1，每个网格块被分成为10个区。这种隐式装配方法具有较好的重叠网格装配效果，插值边界都尽量远离壁面附近的大梯度流动区域，使插值单元和贡献单元的大小更为匹配，有助于减少插值误差并增加数值计算的稳定性。图5(a)为7301两段翼外形的重叠网格装配结果。共有两个网格块，每个网格块分成8个区。图5(b)是局部放大图，图中绿色的网格单元为插值单元。

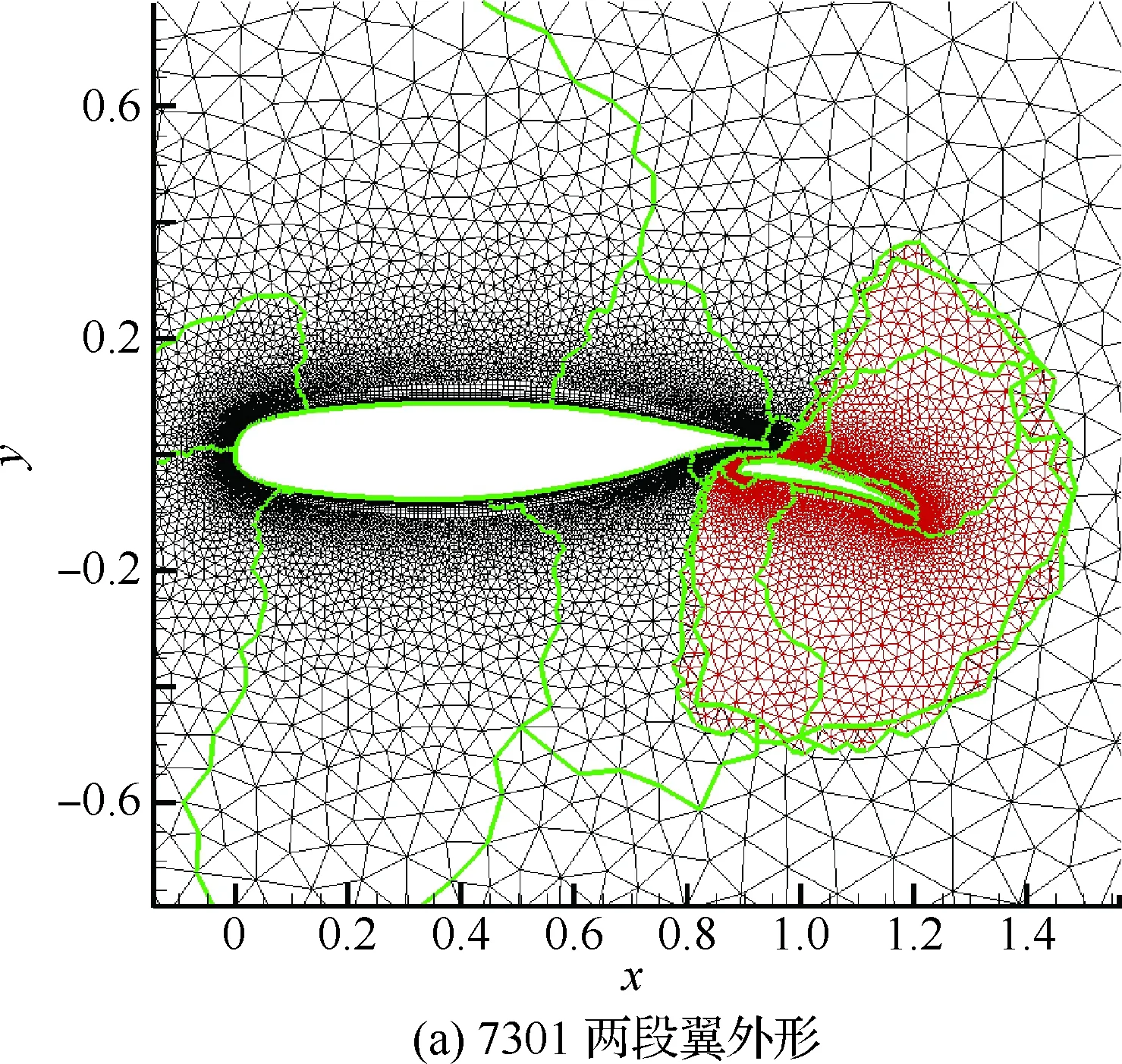
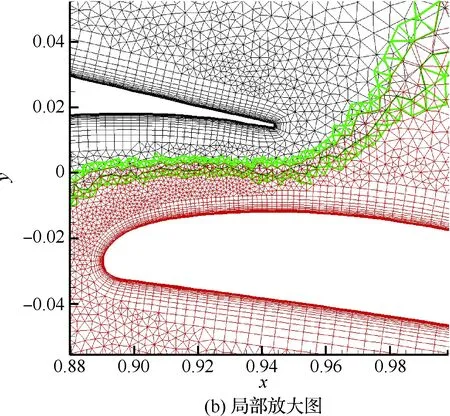
图5 二维非结构重叠网格装配实例(7301两段翼形)Fig.5 Example of assembling of 2D unstructured overset grids (7301 airfoil)

3.2 三维装配实例

图6 三维非结构重叠网格装配算例 (5个圆球)Fig.6 Example of assembling of 3D unstructured overset grids (5 spheres)

图6为三维情况下5个圆球的装配结果。每个圆球网格单元数为120万，背景网格单元数为448万，总体网格单元总数为1 048万。采用该算例对并行网格装配的效率进行了测试。计算机集群采用国产飞腾CPU，主频为1.0～1.5 GHz。首先考虑分区数和进程数相同的情况，表1给出了不同进程情况下的装配时间对比。随着进程数以及分区数的增加，查询节点以及查询插值单元所需的时间单调减少，但是当进程数增加以后，各个进程之间需要通过广播通讯建立整体的网格点集，搜集计算点所需的时间会有所增加。在1 152个分区和进程情况下，完成装配过程所需时间为4.78 s。表2为分区数和进程数不同的情况，网格分成为1 152个分区，采用不同的进程进行装配。查询节点和单元所需时间随着进程数增加而单调减少，但是当进程数增加到一定程度之后，查询所需时间趋于一个定值，而由于搜集计算点所需时间随着进程数增加而单调增加，最终导致并行效率降低，原因在于：① 算法中引入了一些优化措施，通过对zone进行预判断，对于不在重叠区或者最小盒子与其他zone不重叠的zone，将直接跳过而不参与查询，因此导致负载不平衡；② 根据第2节的效率分析，由于网格单元、分区区域大小的不均匀，每个zone里面查询的计算量是不同的，计算最耗时的zone决定了并行装配的最少时间。因此，重叠网格装配算法本身是导致并行效率不高的主要原因，文献[18,24]的并行装配方法在进程数增加后也会遇到相同的问题。因此，如何改进并行装配策略，提高其并行计算效率，仍然是一个需要进一步研究的内容。

在上述算例的基础上，通过增加每个block的网格量以及圆球数量，对更大规模的计算网格进行了并行装配测试。图7为装配结果示意图，网格单元总数为1.23亿，采用了10 968个分区，采用1 024个进程并行装配，完成整个装配所需时间为39.76 s，说明该方法已经具备了大规模网格高效自动化并行装配能力。

进一步耦合求解六自由度动力学方程、非定常流动控制方程，采用机翼外挂物投放的标准算例对重叠网格技术以及耦合算法进行测试。计算软件为自主研制的通用CFD软件平台“HyperFLOW”[25-26]，其中的非定常计算方法见文献[27-28]，这里不再赘述。图8所示为机翼以及外挂物的初始计算网格，物面采用了三角形和四边形单元离散，空间网格有三棱柱、金字塔、六面体、四面体等单元类型。机翼网格单元总数为320万，外挂物单元总数为360万。网格共分成为768个分区，采用128个进程并行计算，在主频为1.0～1.5 GHz的集群系统上，单步重叠网格装配所需总时间约为7 s。

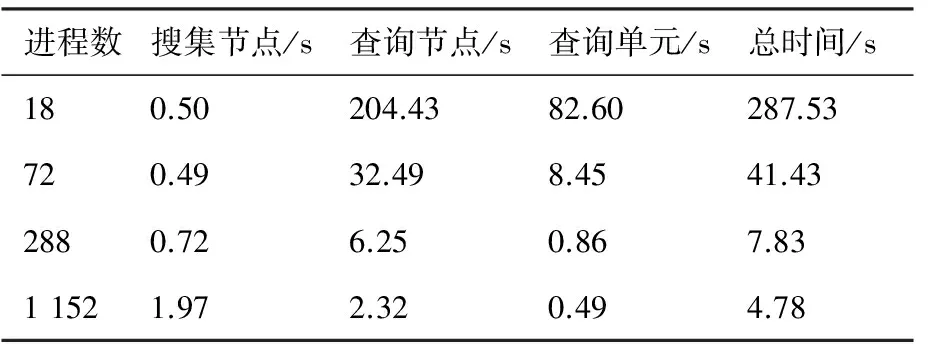
表1 装配时间对比(分区数和进程数相同)Table 1 Comparison of assembling time (same numbers of sub-zones and processors)

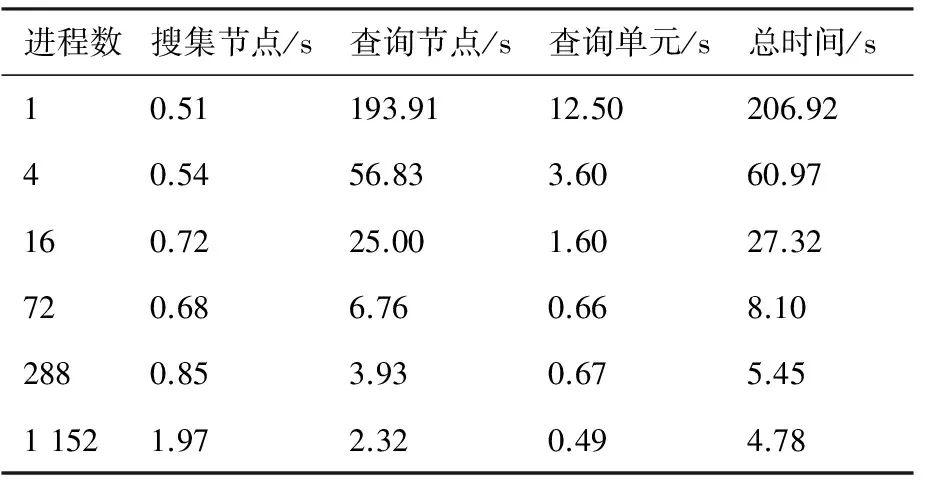
表2 装配时间对比(分区数和进程数不同)Table 2 Comparison of assembling time (different numbers of sub-zones and processors)

分离计算条件详见文献[29]，图9所示为分离过程中典型时刻的动态重叠网格，其中绿色区域为外挂物网格的插值边界；图10为外挂物的运动学参数以及气动力系数，图中各变量定义如下：dx、dy、dz为质心位移；Vx、Vy、Vz为质心运动速度；CA、CY、Cn分别为轴向力、侧向力、法向力系数；φ、θ、ψ分别滚转角、俯仰角、偏航角；p、q、r分别为滚转角速率、俯仰角速率、偏航角速率；Cl、Cm、Cn分别滚转力矩、俯仰力矩、偏航力矩系数。图中实线表示本文计算结果，离散点表示试验结果，计算结果与试验结果吻合较好。图11所示为3个典型时刻的物面压力p云图(无量纲压力，以来流的动压为参考值)，激波干扰等现象捕捉较好。

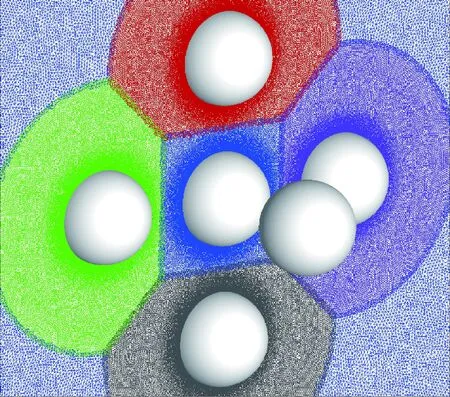
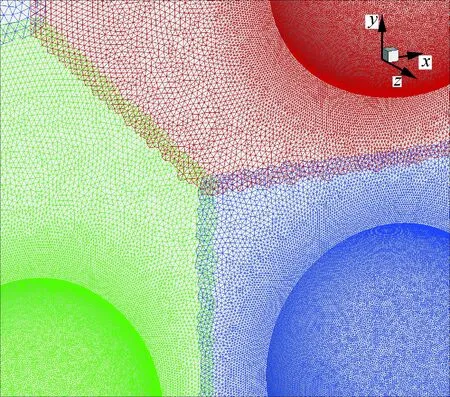
图7 大规模非结构重叠网格装配算例 (6个圆球)Fig.7 Example of assembling of large scale unstructured overset grids (6 spheres)

图8 机翼以及外挂物的初始计算网格Fig.8 Initial computation grids over wing/store configuration

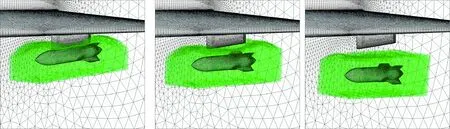
图9 机翼及外挂物分离过程中的动态重叠网格Fig.9 Overset dynanic grids over wing/store configuration during store separation

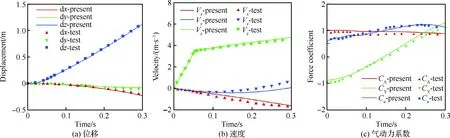
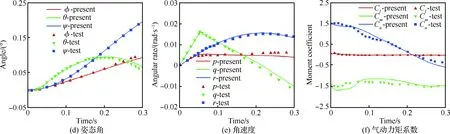
图10 分离过程中外挂物的运动学参数以及气动力系数Fig.10 Kinematic parameters and aerodynamic coefficients during store separation

图11 分离过程中3个典型时刻的物面压力云图Fig.11 Surface pressure contours during store separation at three typical time

4 结 论

建立了一种并行化的非结构重叠网格隐式装配技术。采用壁面距离作为判断插值边界的准则，并采用物理边界推进的方式快速确定出活跃区域，避免了隐式装配方法中的“孤岛”问题。采用分区并行的思路实现了隐式装配技术的并行化，所采用的并行计算策略有助于提高网格装配效率并减少内存消耗。效率分析以及针对实际问题的装配结果表明，该技术能够适用于多块重叠网格，自动化程度较高，装配效果较好，能够推广应用于超大规模计算网格。

然而随着进程数的增多，查询算法所占时间比重逐渐减少，此时并行通讯所占的比重增多并逐渐成为影响装配效率的一个关键问题。本文的并行装配方法在并行效率上仍有较大的改进空间，下一步工作中将针对算法中影响并行效率的诸多细节问题如单元属性通讯、节点搜集等进行细致分析和改进，进一步提升该方法的适用性。