媒介取食偏好和宿主群落组成对多宿主-媒介系统疾病风险的影响
2022-06-20陈立范陈师亮王宏杰宋如意
陈立范,陈师亮,王宏杰,宋如意
(1.上海健康医学院文理教学部,上海 201318)(2.复旦大学生命科学学院,生物多样性与生态工程教育部重点实验室,上海 200433)
媒介传播疾病(vector-borne infectious disease)是指通过蚊、蚤、虱、蜱、蝇等媒介(vector)进行传播的自然疫源性传染病,例如疟疾、莱姆病和西尼罗河病毒等. 据世界卫生组织估计,由于媒介传播的疾病而造成的人类死亡人数每年超过150万,特别是发展中国家的儿童[1]. 媒介传播疾病也给畜牧业和野生动物保护带来了巨大的威胁[2]. 因此,明确影响病原体传播的关键因素不仅对于建立理论分析模型,而且对于疾病的监控和预防都是非常关键的.
对于很多媒介传播疾病而言,病原体可以通过媒介感染多个宿主物种(如西尼罗河病毒、莱姆病等),宿主也可以被多种病原体所感染,这就导致宿主、媒介和病原体之间形成非常复杂的相互作用[3]. 因此,当生物多样性发生改变时可能会对疾病的传播动态产生影响. 目前对于生物多样性和疾病风险之间的关系,主要有稀释效应(dilution effect)和放大效应(amplification effect)两种观点[4-5]. 稀释效应是指生物多样性与疾病风险之间负相关,即保护生物多样性可以降低疾病的爆发和传播风险. 这一概念最早是在莱姆病的研究[6]中被提出的,随后在西尼罗河病毒[7]、两栖类吸虫病(ribeiroiaondatrae)[8]、大麦黄矮病毒[9]和叶片真菌病害[10-11]等多个跨类群的生态系统中得到证实. 如果稀释效应是普遍存在的,那么保护生物多样性将为野生生物保护和公共卫生领域的双赢提供一种可能性[12-16]. 然而,近年来越来越多的学者对稀释效应的普适性提出质疑[15-16]. 一些学者认为疾病的传播涉及到多个营养级之间的相互作用,是一个非常复杂的过程,还会依赖于宿主、传播媒介和病原体的特异性,因此稀释效应并不是一个普遍的现象,只在特定的条件下发生[17]. 还有一些研究结果表明宿主多样性的改变对疾病风险无显著作用[18]或产生放大效应[19]. 这一争议预示着可能会有很多因素影响多样性-疾病关系,这些因素所起的作用是不同的,甚至可能是相反的[20-22]. 然而,到目前为止究竟哪些生态学因素能够影响这一关系以及如何影响尚未得到充分的研究. 找出影响生物多样性-疾病关系的因素并预测在哪种情况下会发生稀释效应,这不仅是传染病生态学研究的核心问题之一,同时也关系到是否可以把保护生物多样性视为控制疾病的一种有效方法.
近年来,多宿主传染病理论模型被应用到多样性-疾病关系的研究中,但是这些理论模型非常笼统,并且大多数是针对直接接触传播的疾病,采用SIR模型为理论框架进行建模. 例如,Keesing等[4]利用SIR模型探究了参数的变动对疾病风险的影响,提出了多样性影响疾病风险的5种机制;Dobson[23]建立了一个多宿主的SIR模型来研究宿主多样性与疾病爆发风险之间的关系. 然而,大多数关于生物多样性-疾病关系的实证研究是在媒介传播疾病中进行的,但是这方面的理论研究却非常匮乏[24-25]. 一方面这可能是由于媒介传播疾病系统不仅涉及到多个宿主物种,还涉及到媒介和宿主的相互作用,系统动态会非常复杂;另一方面在建模时还需要考虑一些现实的因素,如在很多实证研究中发现媒介在取食不同的宿主,甚至同一宿主的不同个体时会表现出取食偏好性(feeding preference),这种偏好性会影响疾病的爆发和传播[25-27]. 此外,一些实证研究还发现宿主群落组成的变动也会影响疾病动态[8,28]. 事实上,宿主群落组成的变动不仅涉及到物种丰富度还涉及到物种均匀度的改变,因此可以反映出宿主多样性的改变. 如果群落组成的某种变动使得媒介接触传递疾病能力较强的宿主(简称强宿主high competence hosts)的几率增加,那么疾病的风险也会增加. 例如,Norman等[29]在研究羊跳跃病(louping ill virus)时发现,红松鸡(lagopusscoticus)是传递该种疾病能力较强的宿主,而野兔(lepus)则是能力较弱的宿主,在不改变宿主物种丰富度的前提下,只改变两种宿主物种的比例(即均匀度),当弱宿主(野兔)所占的比例增加时,疾病的强度会降低.
综上所述,本文将通过理论建模分析和模拟,将多宿主-媒介传播模型纳入到生物多样性-疾病关系的研究中,重点探究媒介的取食偏好性和宿主群落组成的改变这两种生态学因素如何影响疾病风险. 宿主群落组成的变动这一指标既包含了物种丰富度也包含了物种均匀度的改变. 希望通过本研究,进一步找出影响多样性-疾病关系的关键因素,明确稀释效应和放大效应的发生条件,为目前关于稀释效应的争议提供科学合理的解释,并为自然界中控制疾病和制定干预政策提供理论依据.
1 模型与方法
1.1 模型构建
采用传统的“仓室”模型[30]为理论框架来描述两种宿主和一种媒介的病原体传播过程. 假设每一种宿主物种都有易感者、感染者和恢复者三种状态,而媒介物种只有易感者和感染者两种状态. 两种宿主之间没有竞争和捕食相互作用,病原体只能通过媒介感染这两种宿主,媒介对这两种宿主有不同的取食偏好[25]. 模型的具体形式如下:
(1)
式中,Si,Ii,Ri分别表示宿主i的易感者、感染者、恢复者的数目(i=1,2),Sv和Iv表示媒介v的易感者和感染者数目,Ni和Nv表示宿主i和媒介v的数目.由于是媒介传播的疾病,故采用频率依赖的疾病传播方式,kipiSiIv/Ni代表单位时间内被病媒感染的宿主i的数目(即新感染的宿主i的数目),(k1q1I1/N1+k2q2I2/N2)Sv代表单位时间内被染病宿主感染的媒介v的数目.其他参数及其含义详见表1.

表1 参数及其含义Table 1 Parameter assignments and definitions
1.2 模型分析
本研究采用基本再生数R0作为疾病风险的度量,它的含义是在发病初期,当所有个体均为易感者时,一个感染者在其平均患病期内所传染的个体数目.通常,当R0>1时,无病平衡点是不稳定的,疾病将存续而形成地方病,而当R0<1时,无病平衡点是局部渐近稳定的,疾病将逐步消失[30].计算基本再生数比较常用的方法是通过计算无病平衡点处的Jacobian矩阵的主特征值得到[31].假设平衡态时媒介的总数目记作V,则方程组(1)在无病平衡点处对应的Jacobian矩阵为
(2)
通过计算式(2)的主特征值,得到基本再生数为:
(3)

很多以往的媒介传播疾病中媒介对宿主的叮咬率是采用经典的Holling II型功能反应函数来表示[24,32].假设宿主密度足够高,使得媒介有充足的食物来源,并且媒介对这两种宿主物种处理时间相等,那么叮咬率ki可以表示为:
(4)
式中,α1和α2分别表示媒介对宿主1和宿主2的取食偏好率,α1+α2=1,c是媒介总的叮咬率.由于本文的目的之一是探究群落组成的改变如何影响R0的取值,因此模型的参数中需要体现出物种丰富度或均匀度的改变.为此,若令N代表群落中总的宿主个体数目,令x表示宿主1所占的比例(0 (5) (6) 其次,为了进一步简化式(3),引入无量纲化参数γ,令 (7) 从表达式中可以看出,参数γ表示宿主2相对于宿主1的疾病传播率(简称传播比).若γ>1,则宿主2传递疾病的效率比宿主1高,反之亦然.将以上式(5)-(7)代入基本再生数的式子(3)中,可以得到: (8) 不失一般性,在后续的讨论中均假设β≥1,即媒介更加偏好取食宿主2.将式(8)两边同时对x求导,得到: 令上式等于0,整理后得到 (9) 式(9)等价于(1-γβ2)(1-β)x=β(1-γβ2)-2(1-β)γβ2, 当β≠1或γ≠1时解得: 当x>xm时,R0′<0,反之当x 由于本文中x所代表的实际意义是物种1所占的比例,因此x只能介于[0,1], (10) R0(x)在[0,1]上非单调的,先递增后递减,此时既有稀释效应也有放大效应. 当xm≥1或xm≤0或xm∈φ时,即 (11) R0(x)在[0,1]是单调的,要么单调递增,要么单调递减,此时只能发生稀释效应或者放大效应的一种. 式(10)等价于: (12a) (12b) (12c) 同理,式(11)对应的不等式组的解集为: (13a) 或者 (13b) (13c) 当参数β和γ落在白色区域时,式(10)成立,R0(x)是非单调的. 而当参数β和γ落在黑色区域时,式(11)成立,R0(x)是单调的. 在白色圆点处(β=1,γ=1),R0(x)是一个常数.图1 R0(x)的定性行为依赖于媒介取食偏好比β和宿主传播率比γ这两个参数Fig.1 The qualitative behavior of R0(x)dependson the values of the vector preference ratio βand the host transmission ratio γ 为了更加清晰地描述满足不等式组式(12)和式(13)的参数取值范围,给出了图1.当参数落在白色区域时,满足不等式组(12),此时R0(x)在[0,1]上先增加后减少,即先发生放大效应然后是稀释效应;当参数落在黑色区域时,满足不等式组(13),此时R0(x)在[0,1]上是单调的,只能发生稀释或者放大效应中的一种.然而,式(12)和式(13)并不能直观反映出随着群落组成x的变化,媒介对不同宿主的取食偏好比β和宿主的相对传播比率比γ对于R0的影响,为此,基于本文的研究目的讨论以下四类情形: (2)当媒介对两种宿主的取食偏好性相同但两宿主传播疾病的能力存在差异,即β=1,γ≠1时满足式(13b),因此R0随x是单调的.此时,若宿主2为强宿主时(即γ>1),随着x的增加(即弱宿主比例增加),R0是单调递减的,即发生稀释效应;若宿主1为强宿主时(即γ<1),随着x的增加(即强宿主比例增加),R0是单调递增的,即发生放大效应(图2b).综上,当β=1,γ≠1时,R0会随着强宿主所占比例的增加而发生放大效应,随着弱宿主比例的增加发生稀释效应.但不管怎样,最大疾病风险总是在[0,1]的区间端点处取得,即群落中只包含一个物种时取得. (a)β=1,γ=1,R0是个常数. (b)β=1,γ≠1,R0是单调的,若强宿主比例增加则发生稀释效应,否则发生放大效应. (c)γ=1,β≠1,R0是非单调的,先发生放大效应后发生稀释效应. 若被偏好宿主比例增加,则最大值出现的较早,反之则较晚. (d)当β≠1,γ≠1时,若被媒介偏好的宿主为弱宿主时,R0是随x单调变化的,此时当强宿主比例增加时发生稀释效应,否则发生放大效应;若被偏好宿主是强宿主时,R0总是先增加后减少,且最大疾病风险是当x∈(0,1)时取得. 其他参数取值为:c=2,V=200,N=2 000,g1=0,dv=0.05.图2 不同参数组合下,R0与x之间的关系Fig.2 The relationship between R0 and x under different parameter combinations 综上所述,宿主群落组成的改变可能对疾病风险产生稀释、放大或无明显效应三种结果.当媒介对两宿主无取食偏好且两宿主传递疾病的能力相同时,群落组成的变动不会影响疾病风险;当媒介没有取食偏好但两宿主传递疾病的能力存在差异,或者媒介有取食偏好且被偏好取食的宿主恰为弱宿主时,R0是单调的,若强宿主比例增加则发生放大效应,否则发生稀释效应.在这种情况下最大疾病风险总是在群落中只包含一个宿主物种时取得;当两宿主传递疾病的能力不存在差异但媒介有取食偏好,或者当宿主能力存在差异且受偏好的宿主恰好是强宿主时,R0随x的增加先增加后减少,即先发生放大效应然后发生稀释效应,此时最大疾病风险是在两种宿主都存在时取得. 在生物多样性快速丧失的背景下,探究生物多样性的改变对传染性疾病爆发和传播的影响不仅具有现实意义,而且与人类健康息息相关.本文通过构建两宿主的媒介传染病模型,探究了媒介的取食偏好和宿主群落组成的变动如何影响疾病的爆发风险,明确了稀释效应和放大效应的发生条件.结果表明生物多样性的改变对于疾病风险可能产生稀释、放大和无明显效应三种结果,主要取决于媒介对于宿主的取食偏好性和宿主传递疾病的能力的强弱,这在一定程度上解释了目前理论和实证研究中对于稀释效应存在的争议.此外,目前关于稀释效应的理论与实证研究中,较少关注媒介对宿主的取食偏好性这一现象,而本研究的结果恰恰证实媒介的取食偏好性会直接影响到宿主多样性-疾病风险关系的方向和强度.因此,本研究的结果将有助于将媒介的取食偏好性纳入到疾病生态学的理论框架中. 当两种宿主有相同的疾病传播效率时(即γ=1),R0主要是由媒介的取食偏好性决定,存在取食偏好时的疾病风险会高于无偏好时的疾病风险.这一结论在某些野外实验和理论研究中得到过证实,例如研究发现在单宿主群落中(即群落中所有个体传递疾病能力相同),如果媒介对不同宿主个体的叮咬率存在差异,会增加疾病的爆发风险[2].这可能是因为媒介的取食偏好性使得受偏好的宿主获得的叮咬次数更加频繁,当大量的叮咬比较集中在一部分宿主上时,疾病的传播效率会大大增加.而当γ≠1时,若被偏好的宿主为弱宿主时,随着该宿主比例的增加疾病风险会下降.这可能是由于弱宿主的疾病传播能力太低而产生的稀释效应抑制了放大效应的发生.反之,若被偏好取食的宿主是强宿主时,R0是非单调的,最大疾病风险是在群落中存在两种宿主时取得,而不是在包含一种宿主时取得.造成这一结果的原因可能是当媒介对强宿主存在取食偏好时,另外一种宿主的出现,使得媒介对强宿主的叮咬也会比群落中只包含一种宿主时更加集中和高效,因此两种宿主都存在时的疾病风险比只有一种宿主存在时的风险高[24].从图1 的白色区域看出,满足这一条件的参数区域占到了大约50%,因此这一结论似乎适用于很大一部分媒介传播疾病系统. 以往大多数关于生物多样性-疾病关系的研究都是以物种丰富度作为自变量,没有关注均匀度的改变所带来的影响,难以全面反映出疾病风险的变化[33].而本文中所采用的群落组成变动这一指标既包含了丰富度也包含了均匀度的变化信息.但需要注意的是,本文重点是探究物种组成的变动对疾病风险的影响,因此文中所提到的稀释效应和放大效应分别是指随着群落组成的变动(x从0增加到1)能够降低或增加疾病风险的现象,这与以往文献中稀释效应和放大效应的定义是沿着物种丰富度或均匀度梯度降低或增加疾病风险有所不同[4]. 尽管本文中的多宿主-媒介传播疾病模型要比许多真实的自然系统简单得多,例如,本文只考虑了两个物种,并且假设总的宿主密度N与宿主所占比例x是独立的,而在真实的自然界中N往往会随着x增加而增加[24],但是通过这个简单的模型却揭示了宿主多样性与疾病风险之间关系的潜在复杂性[34].更具体地说,本研究不仅定性给出了稀释效应和放大效应的发生条件,而且定量给出了宿主1所占的比例x取何值时疾病风险最高,明确了媒介取食偏好性和宿主的相对传播率这两个生态学因素对疾病风险的影响,丰富和发展了该领域的研究,也为自然界中控制疾病和制定合理的干预政策提供了理论依据.例如,本研究的结论表明当一个种群中的所有个体传播率相近时,对部分个体选择性地使用杀虫剂,会使得媒介比较集中到另一部分个体上,这就相当于媒介具有偏好性取食,因此会增大而不是降低疾病风险.这就提示如果干扰措施运用不当就会取得适得其反的效果.
2 结果与讨论



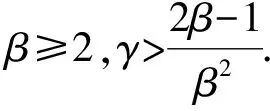

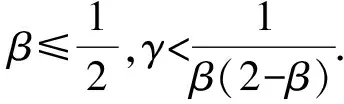
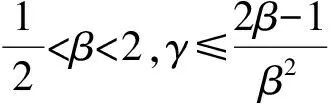


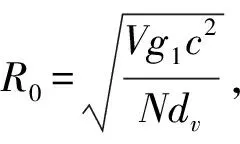
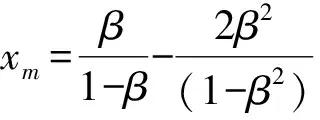


3 结论
