基于VMD和MED的滚动轴承故障诊断方法

郭家宇，熊炘，刘浩

（上海大学 机电工程与自动化学院，上海 200072）

滚动轴承的健康状况影响着整个机械系统的工作状态[1]，通过状态监测和故障特征提取技术了解滚动轴承的运行状态，及早发现故障问题，可以有效提高机械设备的运行水平并降低维修成本。然而，从机械设备现场采集的滚动轴承振动信号由于受严重的背景噪声和其他随机信号干扰，所获信号往往具有非线性、非平稳、非高斯的特征，信噪比较低；特别是齿轮箱中的轴承故障特征信息往往淹没于齿轮啮合频率及背景噪声，严重影响了故障特征信号的识别，用常规的时域分析方法（时域波形分析、自相关分析、峭度指标和波形指标等）与频域分析方法（幅值谱、功率谱、倒谱和包络分析等）难以有效地进行共振频带的选取，无法准确提取故障特征。

时频分析方法[2-6]能够同时再现信号的时、频域特征，对处理非线性、非平稳信号非常有效，但均具有各自的局限性：小波变换可以有效抑制白噪声，但小波基函数和阈值的选择不具有自适应性；经验模态分解（Empirical Mode Decomposition，EMD）方法分析非平稳、非线性信号的能力突出，但其数学基础不严格，模态混叠和端点效应问题表现明显[7]；集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）对 EMD加以改进，在一定程度上抑制了模态混叠的产生，但算法的计算量过大[8]；局部均值分解（Local Mean De-composition，LMD）方法亦存在着模态混叠、迭代计算量大以及端点效应等问题。

变分模态分解（Variational Mode Deconvolution，VMD）可以自适应地分析信号，具有坚实的理论基础和更好的噪声鲁棒性，且相比于EMD，EEMD和LMD等算法，其分解层数少、精度高，不存在模态混叠现象[9-11]。最小熵解卷积（Minimum Entropy Deconvolution，MED）应用于混合多源干扰信号中冲击信号的提取，能有效减弱信号受采集路径而衰减的影响，可以进一步突出振动信号的冲击特征，在滚动轴承故障特征提取中取得了较好的分析效果[12-14]。因此，将VMD与MED相结合，用于提取滚动轴承故障特征，同时与EMD进行比较，通过仿真信号和实测信号验证此方法的有效性及优越性。

1 变分模态分解

变分模态分解是建立在Wiener滤波、Hilbert变换、解析信号、频率混合和外差解调等概念基础上的非递归、自适应的信号处理方法，具有严格的数学基础。其本质是通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽，从而能自适应地实现信号频域的有效分离[15]。VMD算法可解释为变分问题的构造和求解，对输入信号的具体处理步骤可分为变分模型的建立和变分问题的求解2个步骤。

1.1 变分模型的建立

假设输入信号yp（t）是由有限个中心频率不同、带宽有限的离散模态分量 uk（t）（k＝1，2，…，K）组成。通过Hilbert变换将各模态分量uk（t）转换成解析信号，获得各分量单边频谱。接着将各模态分量的解析信号与e-jωkt相乘，各分量频谱被调制到相应基频带。对分量解析信号计算梯度的平方L2范数，估计出中心脉冲频率ωk的带宽。引入约束条件，构建受约束的变分模型为

式中：f为原始信号；uk为模态函数；ωk为各个模态的中心频率；K为模态分量数目。

1.2 变分问题的求解

在上述变分模型中引入α和构造求解无约束性变分问题的增广拉格朗日函数 L（｛uk｝，｛ωk｝，λ），即

式中：α为二次惩罚因子，用于保证处于Gauss噪声下信号的重构精度；λ（t）为Lagrange乘法算子，使得约束条件保持严格性。

利用乘法算子交替方向法（Alternate Direction Method of Multipliers，ADMM）对无约束性变分问题求解，交替迭代更新un+1k，ωn+1k，λn+1，寻找增广Lagrange函数的鞍点，即为（2）式约束变分模型的最优解，从而将原始信号分解为K个窄带本征模态分量[16]。最终求得的更新表达式为

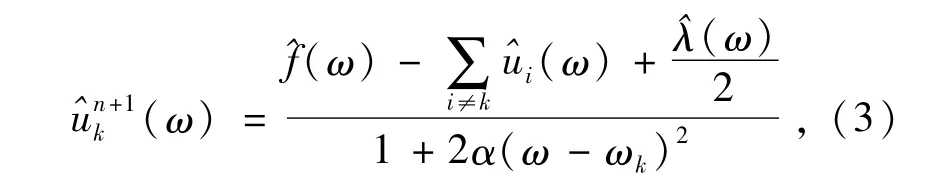
解得中心频率的更新方法为

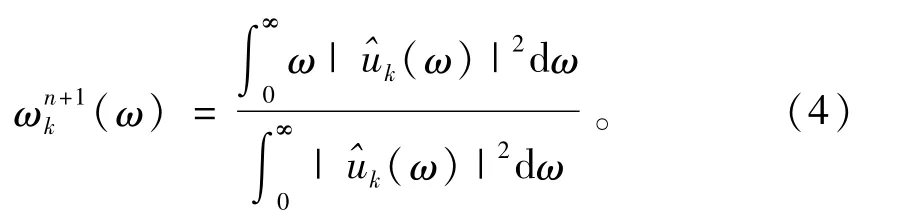
1.3 VMD算法流程

2 最小熵解卷积

滚动轴承振动信号经VMD处理后得到离散模态分量uk（t），为提取信号中较大的尖脉冲成分，恢复原始的输入冲击信号，筛选出和原信号相关系数大的分量进行重构，需要对得到的重构信号进行MED处理。

3 实际验证

3.1 故障诊断流程

综上所述，将VMD和MED相结合，首先，将原始故障采集信号yp（t）进行VMD处理，选取与原信号相关系数大的分量重构；然后，将重构信号y（t）进行MED处理，去除采集路径因素的影响，提高信号信噪比，凸显故障冲击成分；最后，对VMD-MED处理后的滤波信号x（t）采用包络分析，找出信号特征频率，对比轴承故障频率可获得诊断结果。故障诊断流程如图1所示。

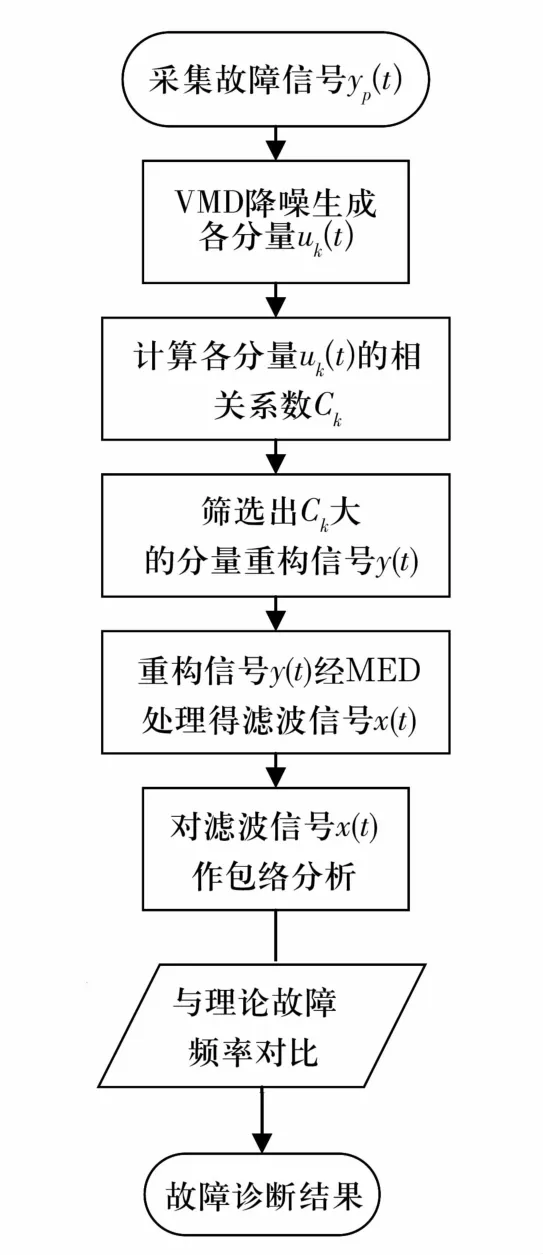
图1 VMD＋MED的故障诊断流程图Fig.1 Flow chart of fault diagnosis of VMD＋MED

3.2 试验条件

滚动轴承故障信号采集自如图2所示的二级齿轮减速器平台，其选用标准直齿轮，齿轮齿数分别为Z1＝32，Z2＝64，Z3＝96，齿轮模数为 1.5。交流电动机输出轴通过联轴器与减速器输入轴连接。振动信号来源于固定在位于减速器输入轴处左侧故障轴承轴承座上端的振动加速度传感器，采样频率为25.6 kHz。试验采用6004-2RSH型深沟球轴承（具体参数见表1），利用线切割方式在轴承内圈沟道上加工宽0.3 mm、深0.2 mm的裂纹故障，从而模拟轴承内圈早期故障缺陷。

图2 二级减速器试验平台Fig.2 Secondary reducer test platform

表1 试验轴承基本参数Tab.1 Basic parameters for test bearing

3.3 轴承故障诊断

试验中，电动机转速为2 400 r/min，即转频fr＝40 Hz，计算可得轴承内圈故障特征频率为fi＝215.6 Hz。选取采样点数为16 384，实际测得内圈微弱故障原始信号及其频谱如图3所示，从时域图中虽然可见部分脉冲冲击，但是其被强烈背景噪声所干扰，无法获取有效故障特征信息；频谱中的高频成分较多，故障特征频率同样难以观察。

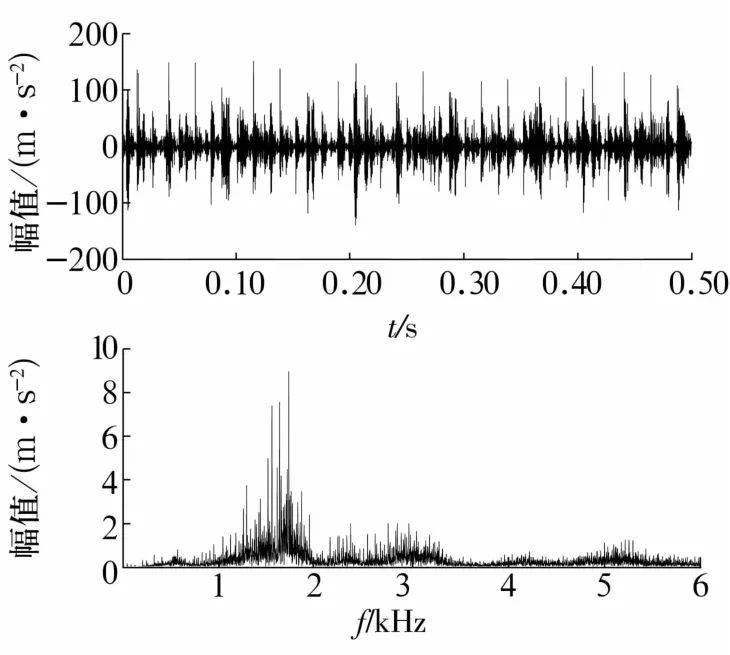
图3 内圈故障原始信号及其频谱Fig.3 Original fault signal of inner ring and its spectrum

考虑到特征频率范围和计算效率，选择分解层数为5层，α采用VMD默认值2 000；τ选为0.3以保证实际信号分解的保真度。内圈故障信号VMD处理结果如图4所示。

图4 VMD分解所得分量Fig.4 Components acquired by VMD

计算各分量与原信号之间的相关系数，计算结果见表2。基于相关系数较大的原则选取V1和V2分量对信号进行重构，降噪后信号的频谱图如图5所示，从图中可以看到信号中的主要高频干扰被滤除。

表2 各模态分量和原信号的相关系数Tab.2 Correlation coefficient between each modal component and original signal

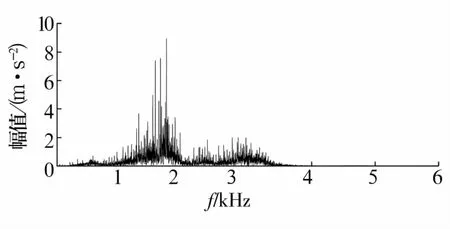
图5 内圈故障重构信号的频谱Fig.5 Spectrum of reconstructed fault singal inner ring

运用MED对经过VMD分解并重构的信号进行处理，所得信号的时域波形如图6所示，从图中可以看到故障冲击信息明显加强。

图6 MED处理后信号时域图Fig.6 Time domain signal after MED processing

为验证VMD＋MED算法的优越性，对内圈故障原始信号采用不同算法进行处理，结果如图7所示。从图中可以看出：图7a和图7b均能提取出内圈故障特征频率及其1～4倍频，而图7c中则清晰可见内圈故障特征频率及其1～9倍频，说明经过VMD和MED方法处理后的信号包络谱能够凸显更多的故障特征频率倍频信息。

图7 内圈故障原始信号的处理结果Fig.7 Processing results of original fault signal of inner ring

进一步对轴承外圈及钢球故障信号进行分析，VMD＋MED算法均可以较好的提取出强背景噪声下滚动轴承的故障信息，且由于VMD的分解层数更少，于滚动轴承故障在线诊断中更具优势。

4 结束语

针对齿轮箱中工作的滚动轴承受强背景噪声和齿轮啮合频率的影响，难以用常规分析方法提取故障特征频率，将VMD和MED相结合，用于提取轴承故障特征信息，经过对齿轮箱故障轴承的振动信号分析表明：VMD降噪时分解层数少且分解精度较高，具有良好的分解效率，信号中的背景噪声能有效地被滤除掉；基于VMD和MED的方法可以有效提取强背景噪声下的滚动轴承故障特征，且相对于基于EMD和MED的特征提取方法提取效果更优。