基于ANSYS的圆柱滚子轴承内圈滚道径向畸变分析

李肖杰，陈观慈，王存珠

（昆明理工大学 机电工程学院，昆明 650500）

圆柱滚子轴承是机械行业的重要基础零部件，径向承载能力较大，几乎不承受轴向载荷，广泛应用于汽车、机床主轴、铁路及航空航天等领域。圆柱滚子轴承与轴过盈配合后内圈滚道会产生变形，轴承内径面形状误差、过盈量及内圈与轴误差相对位置转角会对内圈滚道变形产生重要影响，从而影响内圈滚道的形状误差。而内圈滚道的形状误差会对轴承的精度及力学特性等产生重要影响。文献[1]对轴承的不规则几何尺寸模型的静态特性进行了分析；文献[2]分析了滚道直径误差对轴承振动特性的影响；文献[3]分析了滚道表面波纹度对滚动轴承非线性动力学特性的影响；文献[4]建立轴承理论分析模型分析滚道直径误差对滚子与滚道的接触应力的影响；文献[5]通过建立数学模型分析滚道直径误差对轴承载荷分布的影响；文献[6-7]分析了滚道的几何形状误差及滚子的几何尺寸误差对轴承动力学特性的影响。

鉴于此，在ProE中建立轴-轴承系统误差模型，在建模时通过ProE与ANSYS建立连接，将模型导入到ANSYS中进行仿真分析，分析过盈配合时圆柱滚子轴承内径面形状误差、过盈量、内圈与轴误差相对位置转角对内圈滚道变形的影响。

1 误差模型

假设圆柱滚子轴承内圈内径面及轴的误差形状有椭圆、三棱圆、四棱圆、五棱圆，其误差模型示意图如图1所示，图中，R为内圈理想半径，r为内圈实际半径，δ为误差值（δ＝R-r）。在ProE中建立内圈的误差模型，内圈内径面分别存在椭圆、三棱圆、四棱圆和五棱圆误差，将内圈的误差模型与外圈、滚子装配在一起可得到轴承的三维模型，与轴装配在一起得到轴与轴承的装配模型。将建立的三维模型与ANSYS建立连接得到静态分析模型，在模型中设置约束及边界条件即可得到内圈滚道的变形。

图1 误差模型示意图Fig.1 Diagram of error model

2 有限元建模

以NU1006圆柱滚子轴承为例，其基本结构参数见表1。内外圈及滚子的材料均为GCr15，轴材料为45＃钢，材料参数见表2。

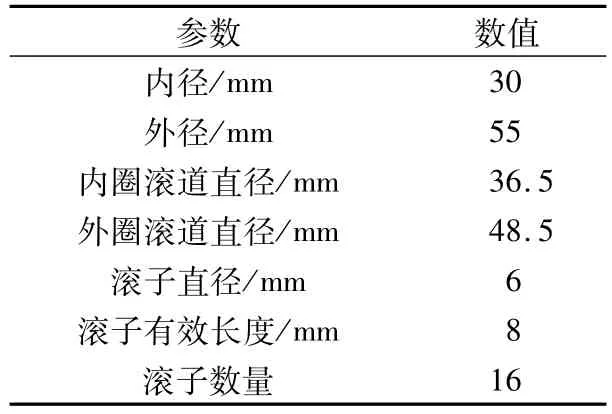
表1 结构参数Tab.1 Structural parameters

表2 材料参数Tab.2 Material parameters

在ProE中建立轴-轴承系统三维模型如图2所示，并导入到ANSYS中。网格划分如图3所示，采用六面体网格进行划分，并对接触部位进行了网格细化，网格划分结果见表3。

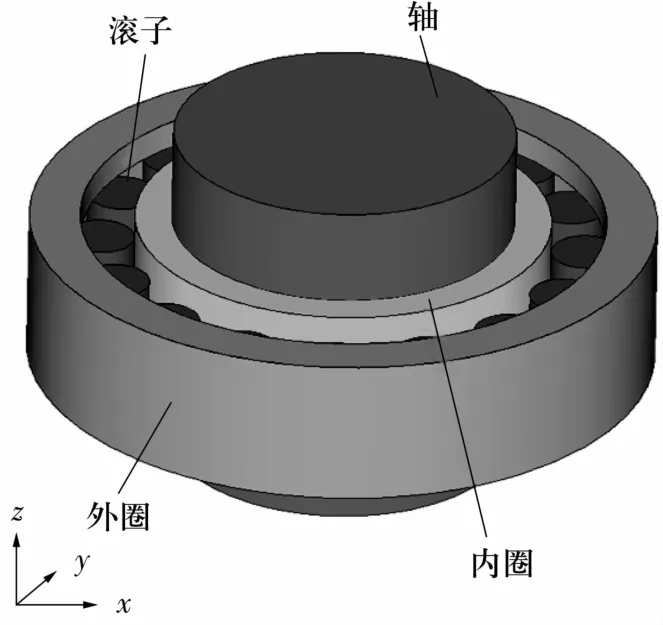
图2 轴-轴承系统三维模型Fig.2 3D model of shaft-bearing system

图3 网格划分Fig.3 Meshing

表3 网格划分结果Tab.3 Results on meshing

模型有滚子与内外圈、滚子与上下挡边以及内圈与轴5组接触对，接触单元选择CONTA174与TARGE170。约束条件如下：1）在轴承外圈轴线上施加全约束；2）约束滚子中间截面绕z向的旋转；3）约束内圈绕z向的旋转；4）约束内圈沿z向的移动；5）在轴中间轴线上施加全约束。

3 轴承内圈滚道径向变形的仿真分析

通过将过盈模型导入到ANSYS进行仿真可以得到轴承过盈配合时轴承内圈滚道的变形云图，再通过MATLAB拟合即可得到轴承内圈滚道中间截面各个位置的径向变形。

3.1 内圈内径面误差值对内圈滚道径向变形的影响

轴有δ＝2.5μm的椭圆、三棱圆、四棱圆、五棱圆误差，内圈内径面误差形状及峰值位置为与之对应的椭圆、三棱圆、四棱圆、五棱圆误差，轴与内圈过盈量为12μm，内圈内径面误差值分别为0，2.5，5.0，7.5μm时内圈滚道的径向变形如图4所示（0°位置为x轴正方向所对应的位置）。由图可以看出：1）当内圈内径面和轴误差值相等均为2.5μm时，变形量波动最小，趋近于一条直线；2）在内圈内径面误差值分别为0，2.5，5.0，7.5μm时，变形量呈周期性波动，且周期数与内圈内径面误差的周期数相同，随轴承内径面误差值的增大，内圈滚道变形量幅值呈增大趋势；3）在误差值为7.5μm时，变形量均为最大，且曲线出现凹点，这是由于滚子与内圈接触，产生接触变形。

图4 内径面误差值对内圈滚道径向变形的影响Fig.4 Influence of error value of inner diameter surface on radial deformation of inner ring raceway

3.2 内圈内径面误差形状对内圈滚道径向变形的影响

轴有δ＝2.5μm的椭圆、三棱圆、四棱圆、五棱圆误差，轴与内圈过盈量为12μm且内圈与轴的误差峰值同为一个方向时，内圈内径面为7.5 μm的椭圆、三棱圆、四棱圆、五棱圆形状误差时内圈滚道的径向变形如图5所示。从图中可以看出，随误差形状的变化内圈滚道的变形量幅值及位置发生变化。如图5a所示，当轴和内圈误差阶次相同时，内圈变形量曲线上的周期幅值不受误差形状的影响，当内圈内径面的误差形状为椭圆时，在 -90°，90°位置处变形量幅值为 4.4μm；内圈内径面为三棱圆误差时，在-55.2°，55.2°位置处变形量幅值为5.1μm，在 -175.5°，175.5°位置处变形量幅值为6.5μm；内圈内径面为四棱圆误差时，在 -141.1°，-51.4°，51.4°，141.4°位置处变形量幅值为7.1μm；内圈内径面为五棱圆误差时，在 176.8°位置处变形量幅值为 6μm，在-34.1°，34.1°位置处变形量幅值为 5.4μm，在-108°，108°位置处变形量幅值为4.7μm。

图5 内径面误差形状对内圈滚道径向变形的影响Fig.5 Influence of error shape of inner diameter surface on radial deformation of inner ring raceway

3.3 误差相对位置对内圈滚道径向变形的影响

轴与轴承过盈配合量为12μm，轴有δ＝2.5 μm的椭圆、三棱圆、四棱圆、五棱圆误差，内圈内径面误差值为7.5μm，误差形状为与轴相对应的椭圆、三棱圆、四棱圆、五棱圆误差，内圈相对于轴的误差峰值的转角分别为 0°，30°，60°，90°时内圈滚道的径向变形如图6所示。由图可以看出，随转角的增大，变形量幅值及位置发生了偏移。如图6a所示，当轴和内圈误差形状为椭圆，轴相对内圈转动0°时，在 -96.4°，96.4°位置处变形量幅值为4.7μm，在 -90°，90°位置处变形量幅值为4.4μm；轴相对内圈转动30°时，在 -101°，101°位置处变形量幅值为5.1μm；轴相对内圈转动60°时，在 -103.5°，103.5°位置处变形量幅值为 6 μm；轴相对内圈转动 90°时，在 -94.5°，94.5°时变形量幅值为6.6μm。

图6 内圈与轴误差相对位置转角对内圈滚道径向变形的影响Fig.6 Influence of error relative position angle between inner ring and shaft on radial deformation of inner ring raceway

3.4 过盈量对内圈滚道径向变形的影响

轴有δ＝2.5μm的椭圆、三棱圆、四棱圆、五棱圆误差，内圈内径面误差值为7.5μm，误差形状为与之对应的椭圆、三棱圆、四棱圆和五棱圆，内圈与轴的误差峰值对应，过盈量分别为3，6，9，12μm时内圈滚道的径向变形量如图7所示。由图可以看出，随过盈量增大，内圈滚道的径向变形量幅值增大。如图7a所示，过盈量分别为3，6，9，12μm时变形量幅值分别为1.3，2.6，3.8，4.7μm。过盈量为12μm时，曲线出现凹点，滚子与内圈滚道接触，产生接触变形。

图7 过盈量对内圈滚道径向变形的影响Fig.7 Influence of magnitude of interference on radial deformation of inner ring raceway

4 结束语

以NU1006圆柱滚子轴承为例，在ProE中建立轴和轴承过盈配合模型，将过盈模型导入到ANSYS中进行分析。最后通过MATLAB对数据进行分析处理，得到轴承内径面形状误差、内圈与轴误差相对位置转角、轴承与轴配合的过盈量对轴承内圈滚道变形的影响。分析结果可为圆柱滚子轴承滚道形状误差的分析提供参考，但轴的误差值及误差形状对内圈滚道变形的影响还未分析，后续有待进一步研究。