硅橡胶圆柱表面与光滑表面接触特性研究
2018-07-22董吉义王友善张传兵粟本龙崔志博
吴 健,董吉义,王友善,张传兵,粟本龙,崔志博
[哈尔滨工业大学(威海) 橡胶复合材料与结构研究所,山东 威海 264209]
硅橡胶密封材料以其优异的物理性能和化学性质,被广泛地应用于航空航天、汽车等领域,对保证设备的正常运转发挥了重要的作用。随着航空工业的发展,密封件的种类日益增多[1]。密封性能的好坏,一方面与密封件的结构形式有关,常见的有O形密封圈[2-3]、矩形密封圈[4]、管状密封件[5]等,密封件的结构形式不同,密封特性也不相同;另一方面,与密封材料的接触特性有密切关系。而不论何种结构形式的密封件在使用过程当中,密封界面的橡胶材料大多处于压缩状态。因此,研究压缩过程中密封材料的接触特性具有重要 意义。
近年来,国内外学者针对橡胶接触理论做了较多研究。C.Yang等[6]采用多尺度分子动力学模型研究橡胶接触特性。P.Wagner等[7]基于功率谱密度分解理论建立了橡胶接触的多尺度有限元分析方法,从宏观和微观角度研究了橡胶在粗糙表面的磁滞摩擦规律。陈国定等[8]在硬球体与橡胶弹性体平面接触的有限元分析的基础上,基于接触概率分析建立了橡胶-金属摩擦副的接触模型,分析了摩擦过程中接触载荷、实际接触面积等参数和摩擦力之间的关系。上述研究侧重于分析橡胶在粗糙表面的接触特性,而对于橡胶在光滑表面上的接触特性并不适用。A.D.Roberts等[9]基于表面能量法对橡胶球在光滑玻璃板上的摩擦特性进行研究,得到了可以定量计算摩擦力的方法。内山吉隆等[10]通过摩擦试验研究了不同速度和载荷下橡胶与玻璃透镜接触过程中的变形情况,得到了Schallamach波产生的条件以及其传播特点。B.N.J.Persson等[11]基于建立的橡胶与光滑表面的微观接触模型,揭示了在纳米尺度下原子或分子热运动产生的热波动会使应力产生兆帕级的波动。M.Mofidi等[12]的研究表明,接触界面任何微小的粗糙度都会使橡胶产生粘弹性变形,对滑动摩擦特性影响显著。
但是,现有文献侧重于研究橡胶的摩擦特 性[13],对于准静态压缩过程中的接触特性研究较少,研究手段也较为单一。本工作采用理论分析与试验研究相结合的方式,研究准静态压缩过程中硅橡胶圆柱表面与光滑表面的接触特性。首先,基于Hertz接触理论,建立橡胶圆柱表面与刚性平板的接触模型,推导出接触压力和接触面积的表达式;然后,基于自主开发的橡胶力学特性测试平台,在光滑亚克力板上进行硅橡胶圆柱件的压缩试验,记录接触面积以及接触压力的变化规律;最后,将硅橡胶圆柱件压缩试验数据与Hertz理论计算结果作比较,以验证结论的正确性。
1 理论分析
Hertz理论是经典接触模型的基础,至今仍然是研究表面接触问题的重要理论之一。Hertz接触模型的建立基于以下假设[14]:(1)接触表面充分光滑;(2)接触物体没有相对滚动;(3)应变很小;(4)接触区逼近时,每个固体都视为半空间弹性体;(5)接触物体不传递切向力。本工作采用Hertz接触理论来分析光滑表面上硅橡胶圆柱件的接触特性,接触模型如图1所示,图中R为圆柱体半径,F为压缩载荷。

图1 Hertz接触模型
根据Hertz理论,圆柱与刚性平面弹性接触时,其接触区域可以简化为长度为L、宽度为2a的矩形,接触压力p分布呈半椭圆柱体[15],见式(1):

式中,x为接触点距接触中心的径向距离。当x=0时,接触区域中心所受到的接触压力最大,见 式(2):

式中,E*为等效弹性模量,E*=E/(1 -μ2);E为硅橡胶弹性模量,μ为泊松比。根据接触应力与载荷之间的关系,可得接触区域的半宽a为

因此,接触区域的总面积S为

2 实验
本工作采用自主开发的橡胶力学特性测试平台,对硅橡胶圆柱件进行准静态压缩试验,试验设备及试件装夹如图2所示。试验试样为3种不同材料的航空用硅橡胶圆柱件,压板采用表面光滑的亚克力板。试验在室温下进行,压缩速率取10 mm·min-1。试验过程中先进行5次预压缩,使材料达到稳定状态,再进行正式压缩。记录并保存压缩过程中的压缩量、压缩载荷以及接触面积的变化,每种材料测试5次,试验结果取平均值。

图2 硅橡胶圆柱件压缩试验设备及其装夹
该测试平台通过传感器记录压缩过程中压缩量和压缩载荷的变化,通过光学显微镜可以实时拍摄接触区域,如图3所示。接触面积S由公式(5)得到,其中,S1为参照区域的实际面积,P1为参照区域的实际像素,P为接触区域的实际像素。以试样1在压缩量为2.5 mm时的接触面积计算为例,参照区域面积S1=100 mm2,运用Photoshop软件可得到P1=477 560,P=638 990,代入公式(5)中,得到此时的实际接触面积S=133.8 mm2。


图3 试样1在压缩量为2.5 mm时的接触区域
图4示出了3个试样的压缩载荷随压缩量变化的曲线。可以看出,硅橡胶在压缩过程中表现出材料非线性。相同压缩量下,试样1的压缩载荷最大,表明其所用材料弹性模量最大,试样2其次,试样3最小。
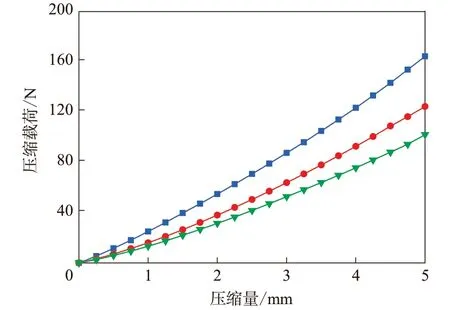
图4 压缩载荷随压缩量变化的曲线
3 结果与讨论
3.1 接触面积
图5示出了硅橡胶圆柱件压缩过程中接触面积的变化规律,其中,压缩载荷F由试验测得,将表1中的数据代入公式(4)可以得到接触面积。从图5可以看出:随着压缩量的增大,接触面积逐渐增大;在压缩初始阶段接触面积增长较快,随着压缩量的增大,其增长幅度逐渐减小。对于不同材料的硅橡胶圆柱件,接触面积随压缩量的变化规律一致;在压缩初始阶段,相同压缩量下,不同材料的圆柱件的接触面积几乎相同,弹性模量对接触面积的影响可以忽略;当压缩量较大时,随着弹性模量的增大,接触面积呈略微减小的趋势,且压缩量越大,这种趋势越明显。
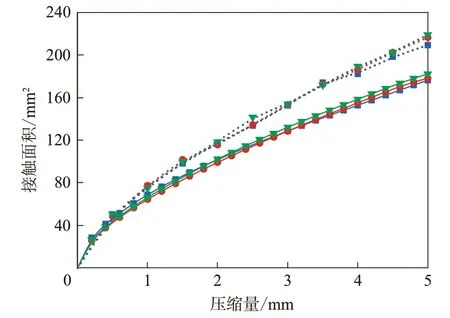
图5 硅橡胶圆柱件压缩过程中接触面积变化规律

表1 Hertz理论计算参数
另一方面,实际接触面积的变化规律与Hertz理论计算结果具有很好的一致性,表明了Hertz理论的适用性。从数值上看,基于压缩试验得到的接触面积大于Hertz理论计算的结果。这是由于在运用Hertz接触理论计算时,所用的接触长度L为圆柱件的初始长度,忽略了压缩过程中的轴向变形;而实际压缩过程中,橡胶圆柱件在轴向也会发生形变,导致接触区域的实际长度L*大于初始长度L,由公式(4)可知,实际接触面积大于理论计算 面积。
3.2 接触压力
不论是静密封还是动密封,接触压力都是评价接触特性的重要指标之一。在静密封中,接触压力越大,一定程度上说明密封性能越好;而对于动密封,为降低密封界面的磨损,应在保证有效密封的前提下尽量减小接触压力。图6为基于Hertz理论计算的压缩过程中最大接触压力的变化规律,由公式(2)计算得到。可以看出,最大接触压力随压缩量的增大而增大,其增长幅度逐渐减小。弹性模量较大的材料在相同压缩量下产生的最大接触压力也较大,表明最大接触压力与材料的弹性模量呈正相关。图7为基于圆柱件压缩试验得到的平均接触压力的变化规律,其中,平均接触压力由压缩载荷及接触面积作商得到。图7表明,平均接触压力的变化趋势与最大接触压力相同;从数值上看,最大接触压力约为平均接触压力的1.5倍。因此,在静密封中,适合采用平均接触压力作为性能评价指标,以保证密封的可靠性;而最大接触压力适用于评价动密封性能,以评估密封性能和磨损程度。

图6 最大接触压力变化规律(Hertz理论计算结果)

图7 平均接触压力变化规律(硅橡胶压缩试验结果)
4 结论
本工作基于Hertz接触理论和硅橡胶圆柱件准静态压缩试验,研究了硅橡胶圆柱表面与光滑表面的接触特性,重点分析了压缩过程中接触面积以及接触压力的变化规律,得到如下结论。
(1)随着压缩量的增大,接触面积逐渐增大,其增幅逐渐减小;相同压缩量下,材料的弹性模量对接触面积几乎没有影响。
(2)最大接触压力随压缩量的增大而增大,其增幅逐渐减小;最大接触压力与材料的弹性模量呈正相关;平均接触压力的变化规律与最大接触压力相同。
(3)Hertz理论计算结果与试验结果具有很好的一致性,表明在本研究应变范围内,Hertz理论适用于橡胶接触特性的研究。
