轮胎微波硫化圆柱谐振腔的设计及数值模拟研究

2018-07-22陈海龙张茂东胡冰涛李庆领

橡胶工业 2018年6期

李涛，孙斌，陈海龙，张茂东，胡冰涛，李庆领

（青岛科技大学机电工程学院，山东青岛 266061）

硫化是轮胎等橡胶制品在制造加工过程中必不可少的一道工序，对橡胶制品的实际应用具有重要意义。微波硫化是一种新型橡胶硫化方式，其硫化快、效率高[1-2]。微波加热最大的缺陷是橡胶内外温度不均匀，因此，设计一种专用于轮胎硫化的微波加热装置具有重要的现实意义。

国内外学者对谐振腔腔体设计进行了相关研究。巨汉基等[3]对影响微波炉性能的各个因素进行了仿真研究。W.Cha-um等[4]利用数值和试验方法对比研究了样品位置、尺寸和微波功率对加热效率的影响。孙鹏等[5]利用有限元分析软件仿真了馈口位置、样品大小、样品位置和多馈口激励时对微波利用率的影响。Y.Huang等[6]运用实验辅助理论的方法分析了规则矩形谐振腔的场均匀性问题。V.Sebera等[7]通过有限元法模拟模式搅拌器对多模腔内微波加热均匀性的影响。杨继孔等[8]对高功率矩形微波反应器加热效率和均匀性仿真进行了研究。曹湘琪等[9-10]对圆柱形微波加热器的效率和均匀性仿真进行了研究，并利用HFSS软件仿真圆柱形微波加热器馈口位置和长度、内筒半径和高度以及负载厚度对微波吸热效率的影响。

迄今为止，国内外学者对用于轮胎微波硫化谐振腔的相关研究较少，仅有少数关于轮胎微波硫化矩形谐振腔的研究，而圆柱谐振腔具有品质因数高、调谐方便、结构坚固和易于加工制作等优点。本工作对轮胎微波硫化圆柱谐振腔进行设计，并对圆柱谐振腔内轮胎微波硫化过程进行数值模拟研究。

1 谐振腔尺寸理论计算

1.1 设计原理

对于圆柱形谐振腔，其谐振频率的计算公式[11]如下：

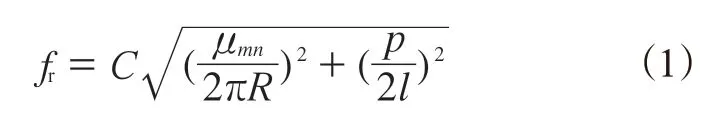
式中，fr为谐振腔的谐振频率；R为圆柱形谐振腔半径；l为圆柱形谐振腔的高度；m，n，p为模式标号，取值为正整数（0，1，2，3，4…），每一种组合称为一种工作模式，其组合数称为模式数；μmn为m阶贝塞尔函数的导函数第n个根植。以上参数均采用国际单位制。

谐振频率只有满足公式（2）[12]时的模式才能在腔体内生成。

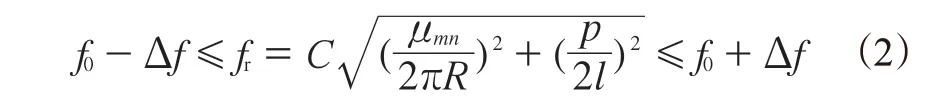
式中，f0为工作频率；Δf为频宽。

确定工作频率和频宽后，对于一定半径和高度的圆柱形谐振腔，可以计算该圆柱形谐振腔的模式数、简并比。通过计算不同尺寸圆柱形谐振腔的模式数、简并比，并从中选择模式数较大、简并比为0的圆柱形谐振腔（此时谐振腔内电磁场分布更为均匀且损耗低）。

1.2 设计过程

（1）确定工作频率和频宽。目前，中国用于工业加热设备的微波固定专用频率为L波段[（915±25） MHz]和S波段[（2 450±50） MHz]。915 MHz型的设备正受到重视，因为橡胶在915和2 450 MHz下的吸收性能并无明显差异，但915 MHz却有透射能力强、投资成本低、功率利用率高、磁控管寿命长、可达功率高和维修较方便等优点。

（2）确定圆柱形谐振腔的尺寸。模拟选用轮胎为7.50R20内支撑外胎，确定圆柱形谐振腔的最小半径为472 mm，最小高度为230 mm。设定R为472～682 mm，ΔR为15 mm；l为230～530 mm，Δl为30 mm。

（3）计算各尺寸腔体的模式数、简并比。根据公式（2）计算不同尺寸腔体的模式数、简并比。

（4）初步确定圆柱形谐振腔尺寸。对计算结果进行筛选，选择模式数大于或者等于9且简并比为0的圆柱形谐振腔，初步确定圆柱形谐振腔尺寸及其对应的模式数和简并比如表1所示。

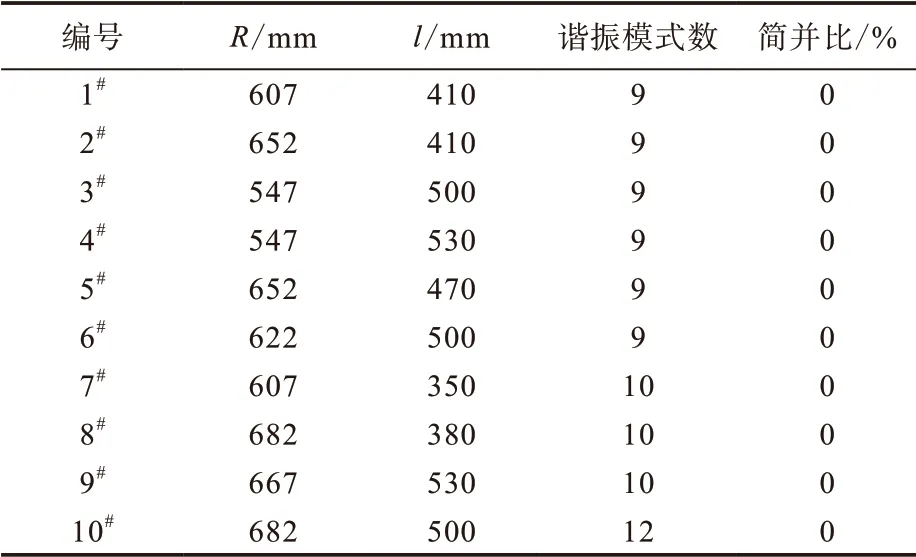
表1 模式数大于8的圆柱形谐振腔尺寸及其对应的模式数和简并比

2 数值模型与物理模型

2.1 模型简化

为节省计算时间和降低CPU使用率，对模型进行合理假设，具体如下：

假设1：构成轮胎的橡胶材料均匀且各向同性；

假设2：介电性能不变；

假设3：轮胎和空气的初始温度均匀；

假设4：传质过程忽略不计；

假设5：空气与轮胎之间的化学反应忽略不计；

假设6：空气的介电损耗忽略不计；

假设7：波导和腔体的材质为铜；

假设8：空气中热传导忽略不计；

假设9：轮胎边界完全绝缘；

假设10：端口由Y方向的横向电磁驻波场激励。

2.2 物理模型

将7.50R20内支撑外胎简化为5层，分别为胎面、胎肩、胎侧、气密层和带束层，轮胎轮廓如图1所示。根据工作频率（915 MHz）选择BJ8型号波导，波导长度定为100 mm，放置在圆柱形谐振腔侧面正中位置。轮胎、谐振腔和波导的相对位置如图2所示。

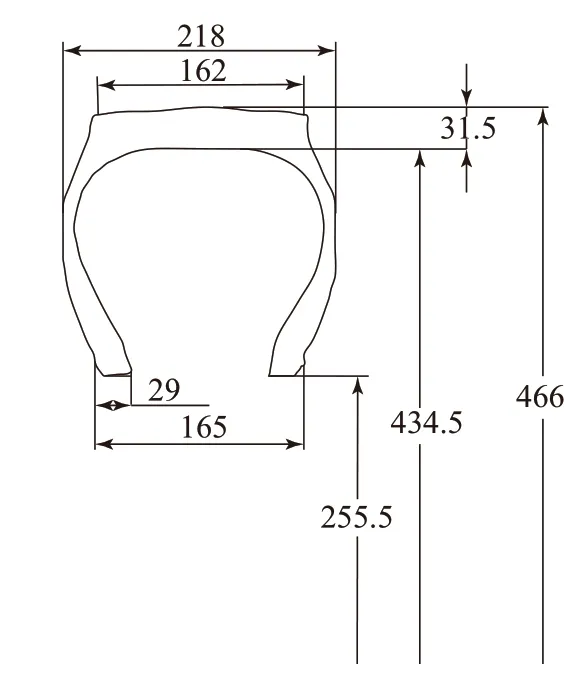
图1 7.50R20轮胎轮廓示意

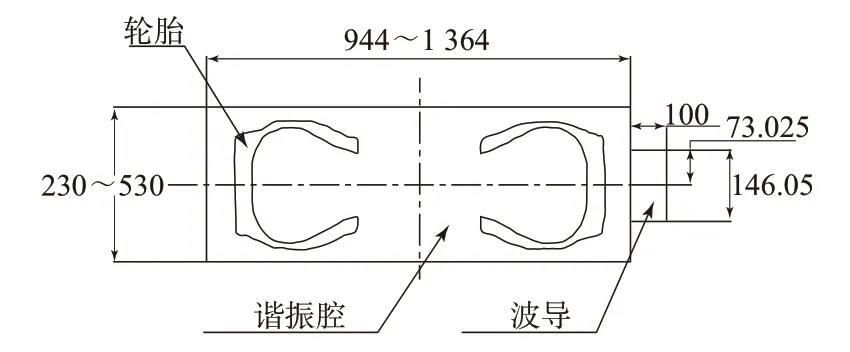
图2 轮胎、谐振腔和波导相对位置示意

2.3 控制方程

COMSOL Multiphysics软件用于轮胎微波硫化过程数值模拟，该数值模拟过程耦合了电磁方程和传热方程。COMSOL Multiphysics软件使用了有限元方法（FEM）的数值计算模型，采用麦克斯韦方程计算数值模拟过程中的电磁传播。电场波控制方程如下：

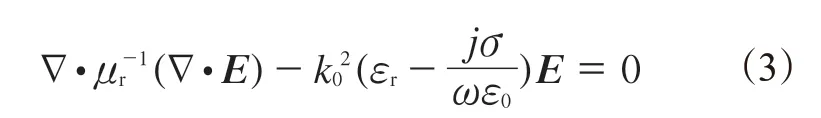
式中，μr为相对磁导率；k0为自由空间的波数；εr为相对介电常数；σ为电导率；ω为角频率；ε0为真空介电常数（8.85×10-12F·m-1）；E为电场强度，V·m-1。

k0根据公式（4）计算：

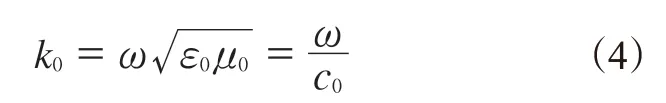
式中，c0为真空光速。

介电常数为复数形式，表达式如下：

式中，ε*为复介电常数，F·m-1；ε′为介电常数实部；ε″为介电常数虚部，F·m-1；j=（-1）1/2。

微波场传热方程用傅里叶能量平衡公式来耦合，表达式如下：

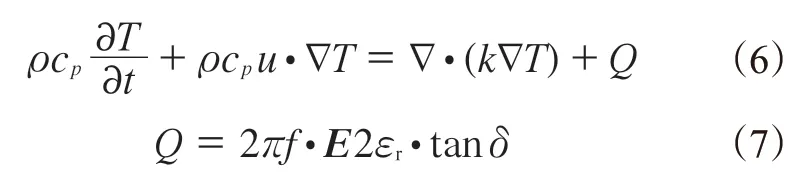
式中，ρ为密度，kg·m-3；cp为常压比热容，J·kg-1·K-1；T为热力学温度，K；k为热导率，W·m-1·K-1；f为频率；δ为介电损耗角；Q为体积热源。

2.4 网格质量

采用物理控制网格构建整个几何体。网格单元尺寸设置为细化。为得到准确的结果，最大网格单元尺寸精细到到微波波长的1/10。轮胎构建网格单元（见图3）数目为153 633。网格单元质量评价如图4所示。根据经验，当单元质量值大于0.6时，数值模拟结果是可靠的。

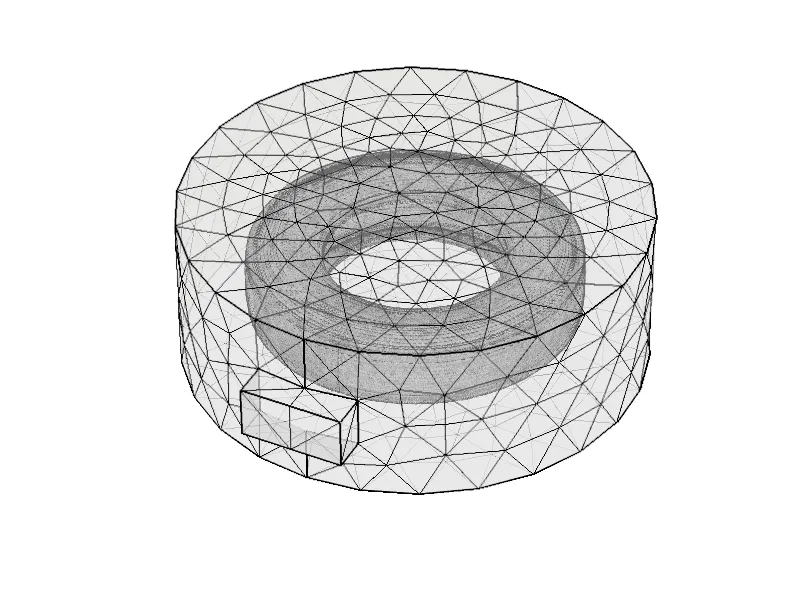
图3 网格单元

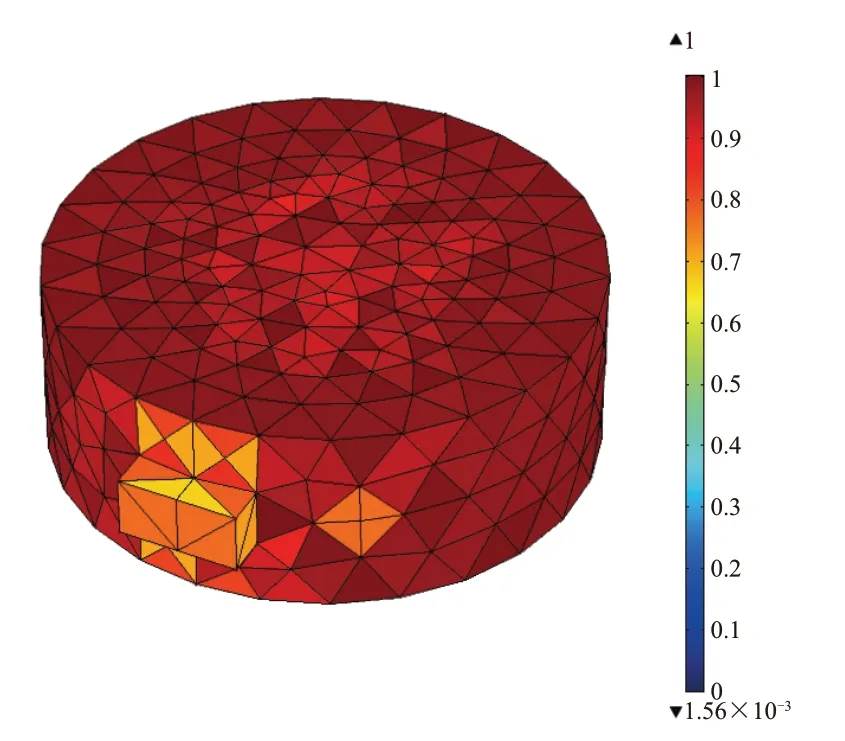
图4 网格单元质量评价

3 试验研究

3.1 微波加热装置

试验选用Milestone Microwave Laboratory Systems系列中的High Performance Microwave Digestion Unit MLS 1200 mega作为加热橡胶的微波加热器（工作频率为2 450 MHz），微波加热器如图5所示。

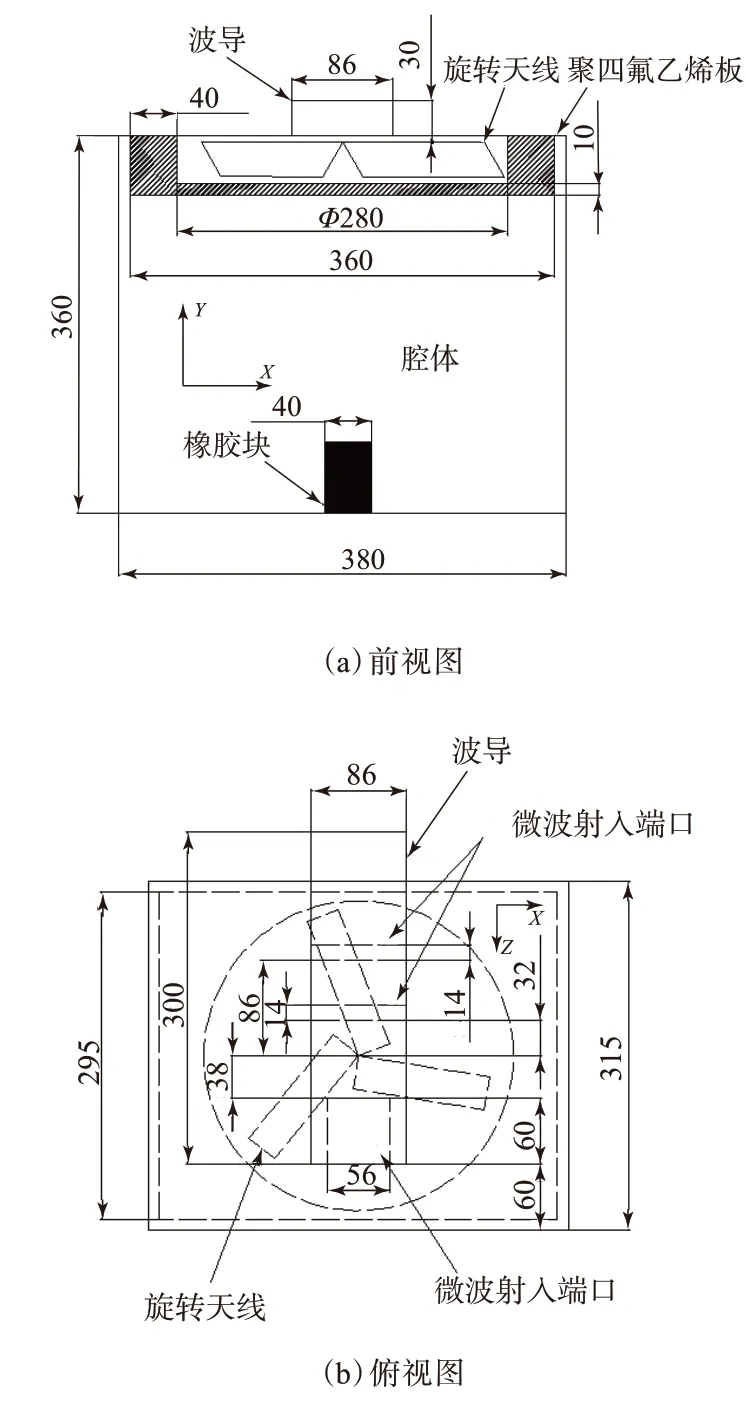
图5 微波加热器示意

微波加热器的主要部件包括谐振腔（微波加热腔体）、磁控管、功率放大器、波导、变压器、电源、炉门、控制面板和通风装置。微波加热器接通电源后，磁控管开始运转，其输出的能量经功率放大器放大后，再通过波导传输，最后由耦合窗耦合到谐振腔中，微波在加热腔体内来回反射从而起到加热物料的作用。该微波加热器的优势在于能够在一个较大范围内对加热功率和时间进行设定，且可以进行功率、时间组合加热条件的设定。

3.2 温度测量装置

通常情况下，采用热电偶、温度计等对物料进行测温，但无论是热电偶还是温度计中都含有金属，将金属放置在微波环境中，会发生打火现象，这使得传统的测温方式束手无措。测温仪器在微波加热橡胶环境中必须满足以下两点要求：

（1）测温元件不受微波强电磁场的影响，能够精确无误测量物料的温度；

（2）测温元件中不含金属材料，并且使用的材料能够耐200 ℃以上温度。

经过筛选，光纤温度传感器和红外热成像仪满足以上两点要求。试验中选用光纤温度传感器实时测量胶片在微波加热时的温度，选用红外热成像仪测量胶片加热后的最终表面温度。试验中所用光纤温度在线检测装置如图6所示，其通过数据线与笔记本电脑连接，测温端与橡胶试样连接，另一端与光纤温度在线监测装置连接。传感器技术参数如下：

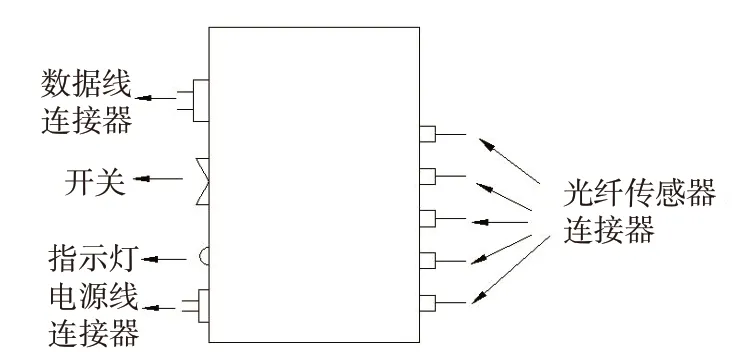
图6 光纤温度在线监测装置示意

电源电压 220 V，测量范围－50～＋200 ℃，测量精度 ±0.5 ℃FS，分辨率 0.1 ℃，采样频率 1 Hz，数字接口 RS485，波特率 9 600 bps，工作温度－40～＋75 ℃。

3.3 橡胶块测温点布置

对不同尺寸的橡胶块（如表2所示）微波加热。为得到微波加热过程中橡胶块的温度分布规律，在橡胶块内布置9个测温点并对测温点标号，如图7所示。

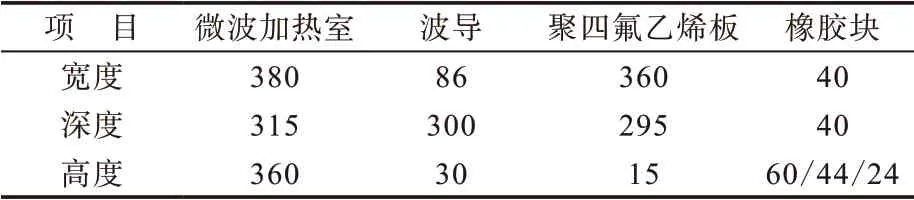
表2 微波谐振腔、波导、聚四氟乙烯板和橡胶块尺寸 mm

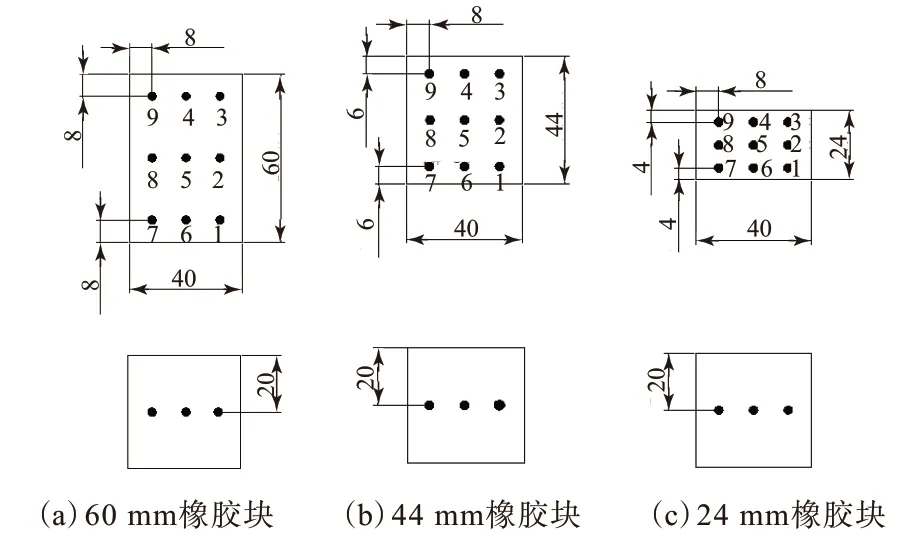
图7 橡胶块测温点布置示意

3.4 试验验证

使用微波加热装置对橡胶块加热并采用光纤温度在线检测装置测量橡胶块内测温点的温度。使用COMSOL Multiphysics模拟橡胶块的微波加热过程。将几个测温点的试验结果和数值模拟结果进行对比，如图8所示。数据分析表明：试验结果和模拟结果中测温点的温升规律相似，模拟数据与试验数据密切相符；所有测温点的模拟数据和试验数据之间的偏差在5%以内，验证了数值模拟模型的可靠性。

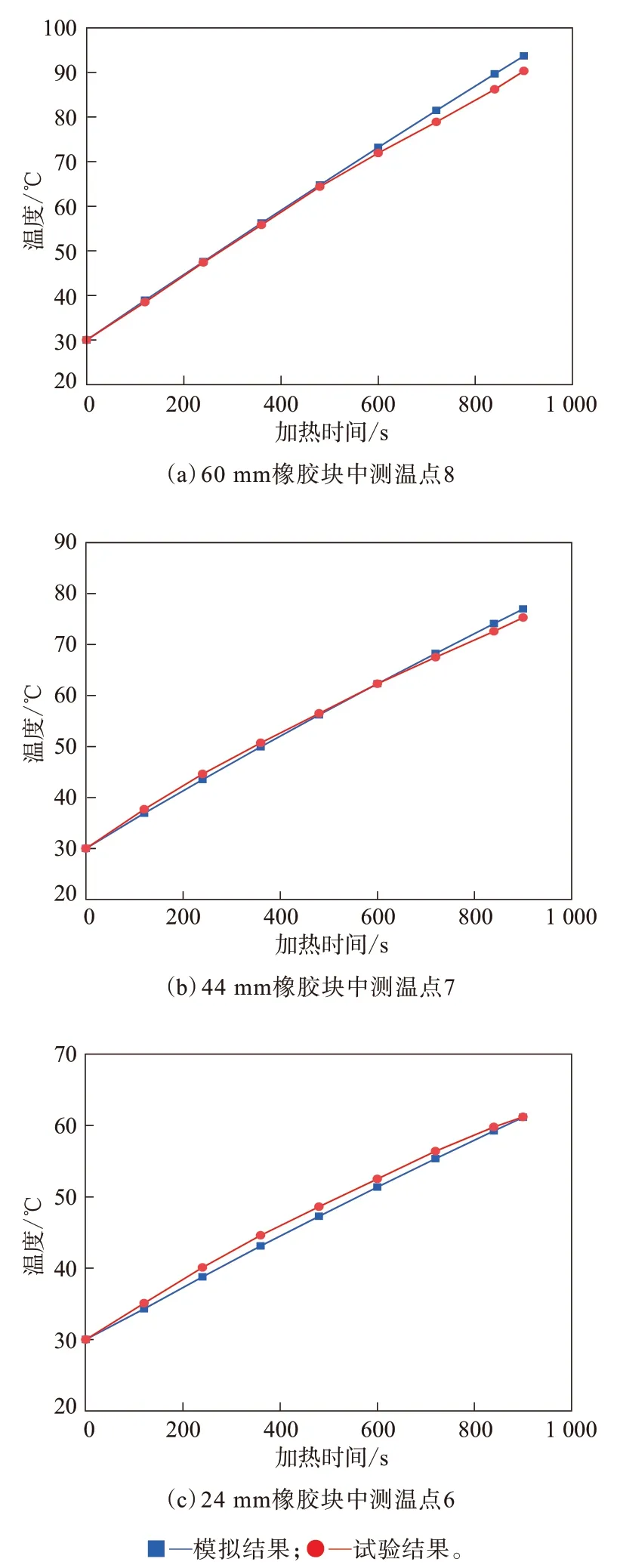
图8 测温点的试验结果和数值模拟结果

4 结果与分析

微波激发频率为915 MHz，模式为TE10，微波输出功率为10 kW。受热的轮胎橡胶初始温度为20 ℃，加热时间为1 800 s。为使7.50R20轮胎加热均匀，让其在谐振腔内进行旋转。对选定的10组尺寸圆柱形谐振腔内的轮胎微波硫化过程进行数值模拟，得到微波作用（加热）720 s时的轮胎温度云图（见图9）。

从图9可以看出，随着模式数增加，轮胎微波硫化的均匀性有所不同，即使同一模式数的谐振腔，轮胎微波硫化的均匀性也有所不同。其中5#谐振腔和6#谐振腔内轮胎温度分布较均匀，最大温差分别为36.3和48.7 ℃；1#，4#和7#谐振腔内轮胎温度分布相对不均匀，最大温差分别为76.9，70.0和105.1 ℃。

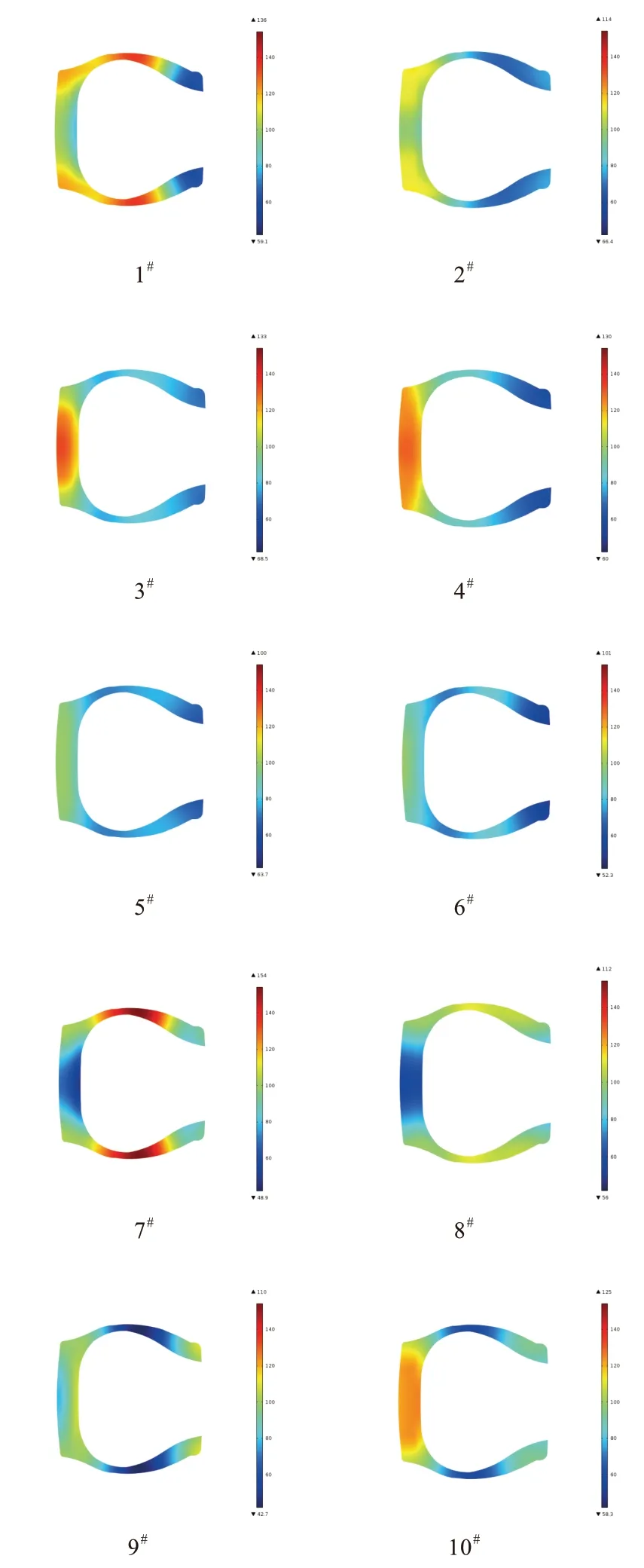
图9 微波加热720 s时的轮胎温度分布云图

模拟得到微波加热720 s时1#—10#谐振腔内轮胎体平均温度、回波损耗S参数和最大温差，通过S=10log（P反射/P入射）对S参数计算，得到各谐振腔的微波利用率。将微波加热720 s时1#—10#谐振腔内轮胎体平均温度、微波利用率、回波损耗S参数和最大温差统计于表3中。

根据表3数据作图，探索微波利用率和轮胎体平均温度的关系，如图10所示。

从表3和图10可以看出，轮胎体平均温度变化趋势与微波利用率变化趋势相同，即随着微波利用率增大而增大，反之亦然，即微波利用率越大，轮胎体平均温度越高。这是因为微波利用率越高，则在相同的加热时间内，轮胎获得的能量越多，轮胎的加热体积就越大，轮胎体平均温度就越高。为了更好地得到微波利用率和轮胎体平均温度的关系，对轮胎体平均温度和微波利用率进行线性拟合，结果如图11所示。

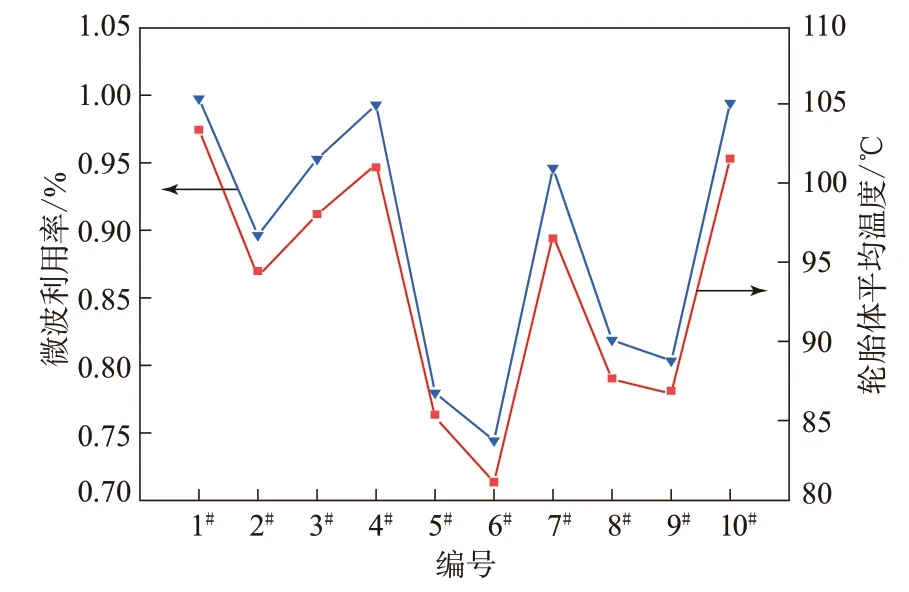
图10 圆柱形谐振腔的微波利用率及其加热720 s时的轮胎体平均温度

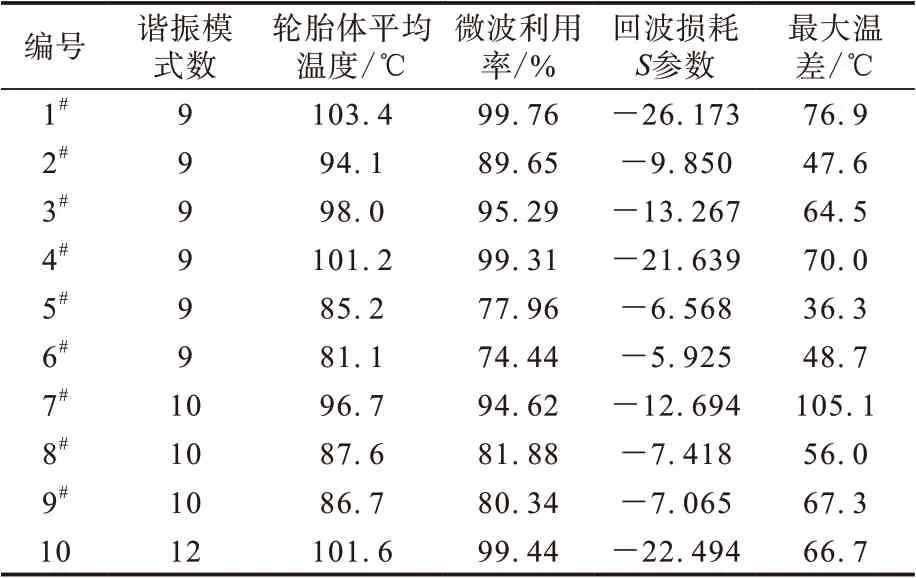
表3 模式数大于8的圆柱形谐振腔性能参数

从图11可以看出，拟合曲线与轮胎体平均温度和微波利用率两组数据切合程度较高，轮胎体平均温度随着微波利用率增大而增大。通过拟合得到y＝80.107x＋22.047，可决系数R2＝0.990 52，这表明拟合曲线能够较好地表征轮胎体平均温度和微波利用率之间的关系，且轮胎体平均温度与微波利用率呈现良好的一次函数关系。

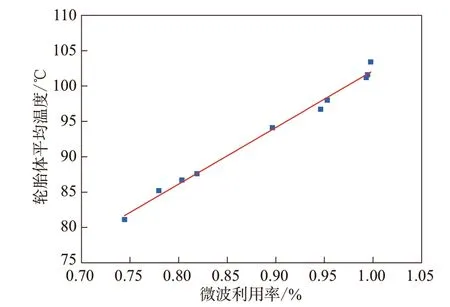
图11 轮胎体平均温度和微波利用率关系的拟合曲线

根据表3中轮胎体平均温度和最大温差数据作图，结果如图12所示。

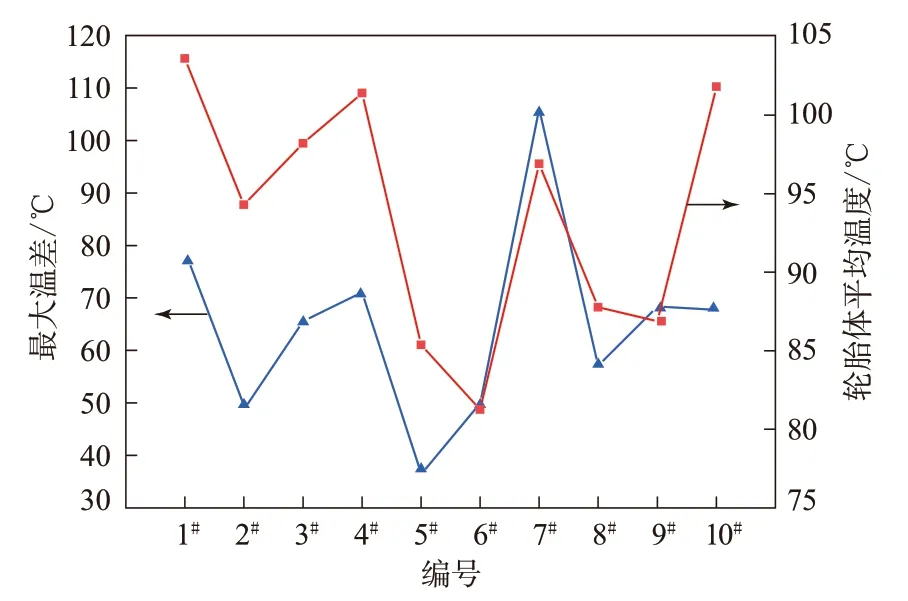
图12 圆柱谐形振腔的最大温差及其加热720 s时的轮胎体平均温度

从图12可以看出：1#，2#，3#，4#，7#和10#谐振腔内轮胎体平均温度均大于90 ℃，微波利用率较大；1#，3#，4#，7#，9#和10#谐振腔内轮胎最大温差大于60 ℃且加热相对不均匀；2#谐振腔的轮胎最大温差较小，轮胎微波硫化不均匀；5#，6#，8#和9#谐振腔内轮胎体平均温度在80～90 ℃，低于其他谐振腔，微波利用率较小；8#和9#谐振腔的轮胎最大温差大于5#和6#谐振腔且轮胎微波硫化不均匀；5#谐振腔内轮胎体平均温度大于6#谐振腔内轮胎体平均温度且轮胎最大温差小于6#谐振腔内的轮胎最大温差，虽然5#谐振腔内轮胎体平均温度较小、微波利用率较低，但轮胎最大温差最小，轮胎微波硫化也最为均匀。为取得更好的加热效果，确定5#谐振腔的尺寸为最终圆柱形谐振腔的尺寸，即圆柱形谐振腔半径为652 mm、高度为470 mm。