基于层次分析法的变权PROMETHEE模型在雨水利用评价中的应用

曾 超， 杨 侃， 刘 朗， 梁永静， 杨 堃， 朱子唯， 卞 雨

(1.河海大学 水文水资源学院， 江苏 南京 210098； 2.句容水利农机局， 江苏 句容 212400)

1 研究背景

水资源短缺是21世纪人类面临的最大的资源问题，如何合理高效地利用现有的水资源是专家学者一直致力的研究方向。雨水资源作为一种较为优质的水资源，容易收集利用，而且污染小，可用作农业灌溉用水、生活用水、工业用水、生态用水以及市政用水，具有涵养水源地、城市防洪和改善生态环境等功能，尤其在水资源匮乏的地区，雨水资源更是一种关键的水资源。总体来看，合理高效地利用雨水资源具有良好的生态、社会以及经济效益。当前，国家大力推进“海绵城市”的建设，“海绵城市”的重点就是如何合理地利用雨水资源，所以进行区域雨水利用的评价是必要的。

目前并没有一种完美的评价雨水资源利用现状的公式或方法，常用的方法有模糊评价法[1]、物元分析法[2]、集对分析法[3]、灰色关联分析法[4]、综合指数法[5]等，这些方法多数用层次分析法确定权重，而层次分析法的主观性较大，若某一较差的指标的权重很小，那么该指标很可能会被较好的指标中和掉，有失评价的公平性。此外，这些方法计算大多比较繁杂，不容易被决策者所理解和接受。本文在参考文献[6]、[7]、[8]和[9]的基础上，提出一种以层次分析法为基础的变权PROMETHEE评价方法，相比其他方法简单易行，不受评价等级的约束，同时变权分析保证了评价的公平性。本文将该方法运用到云南省4个不同区域，得出它们的优劣次序，提出相应的改善意见。

2 雨水资源利用评价指标的确立

影响雨水资源利用效率的因素有很多，在确立评价指标之前需要对这些因素进行筛分，尽量选取能够从不同角度反映雨水利用现状的因素，从而确立雨水利用评价指标。本文综合各类文献后从生态、生产、生活三方面选取的6个指标如下：

(1)雨水资源控制率I1:年人工积蓄雨水总量/多年平均区域降雨量(%)；

(2)农业灌溉用水中雨水所占比例I2:雨水灌溉的耕地面积/区域内耕地总面积(%)；

(3)生活用水中雨水所占比例I3:生活用水中雨水用量/区域内生活总用水量(%)；

(4)工业企业用水中雨水所占比例I4:工业企业用水中雨水用量/区域内工业总用水量(%)；

(5)生态环境用水中雨水所占比例I5:生态用水量中的雨水用量/区域内生态总用水量(%)；

(6)市政用水中雨水所占比例I6: 市政用水量中的雨水用量/区域内市政总用水量(%)。

3 基于层次分析法的变权PROME-THEE评价模型

3.1 PROMETHEE法

PROMETHEE法是一种基于方案的两两比较的多属性决策分析方法，它是建立在“级别优先于”关系上的排序方法[7]。该方法引入优先函数的概念，克服了ELECTRE法属性值之间差距大小的信息缺陷。

(1)优先函数值的计算。对于某个目标或属性，PROMETHEE会给每个方案定义一个优先函数，函数值从0到1。如果用P(xi，xj)表示该优先函数，若函数值为0，表示xi和xj无差异；函数值越接近1，则xi越优于xj；当函数值为1时，表示xi严格优于xj。为了计算方便，可令dij=xi-xj，则可构造优先函数如下：

(1)

式中：dmax为该指标各方案的最大差距。

(2)优先指数的计算。对于每对方案xi和xj，当方案的各指标的权重赋值为wj时(j=1,2,…,m)，定义综合相对优先指数为：

(2)

式中：m为指标的总个数。

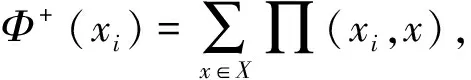
易知Φ+(xi)越大，xi相比其他方案的优先级别越高，Φ-(xi)越小，其他方案比xi优先级别高的可能性就越小。

(4)计算净流。为了得到X上的完全序，可以给每个方案定义一个净流Φ(xi)，计算公式如下：

Φ(xi)=Φ+(xi)-Φ-(xi)

(3)

通过计算可以得到每个方案的净流，通过各方案净流大小的排序可以得到各方案的优劣排序。

3.2 初始权重的确定

本文采用层次分析法确定权重，目标层为雨水利用效率，指标子层为6个评价指标。

3.3 变权模型

层次分析法确定的权重主观性较大，未能与实测数据相结合，某些指标较差，但相应的权重很小，这样综合评价就很可能将这些指标中和掉，使评价缺乏公平性。为此，可以将这些较差的指标的权重适当上调，以示惩罚，保证评价的公平性。

构造惩罚型变权函数如下：

(4)

式中：wj为层次分析法确定的初始权重;xj为该地区指标j相比其他地区的优先度。

这样根据不同方案的各自指标进行变权分析显得更加合理。将变权后的权重运用到PROMETHEE模型中。

4 实例运用

以云南省的4个区域为例，利用基于层次分析法的变权PROMETHEE模型对它们的雨水利用现状进行评价。各地区的雨水利用现状见表1。

4.1 各评价指标初始权重的确定

首先利用层次分析法确定初始权重，各指标的相对重要性见表2。

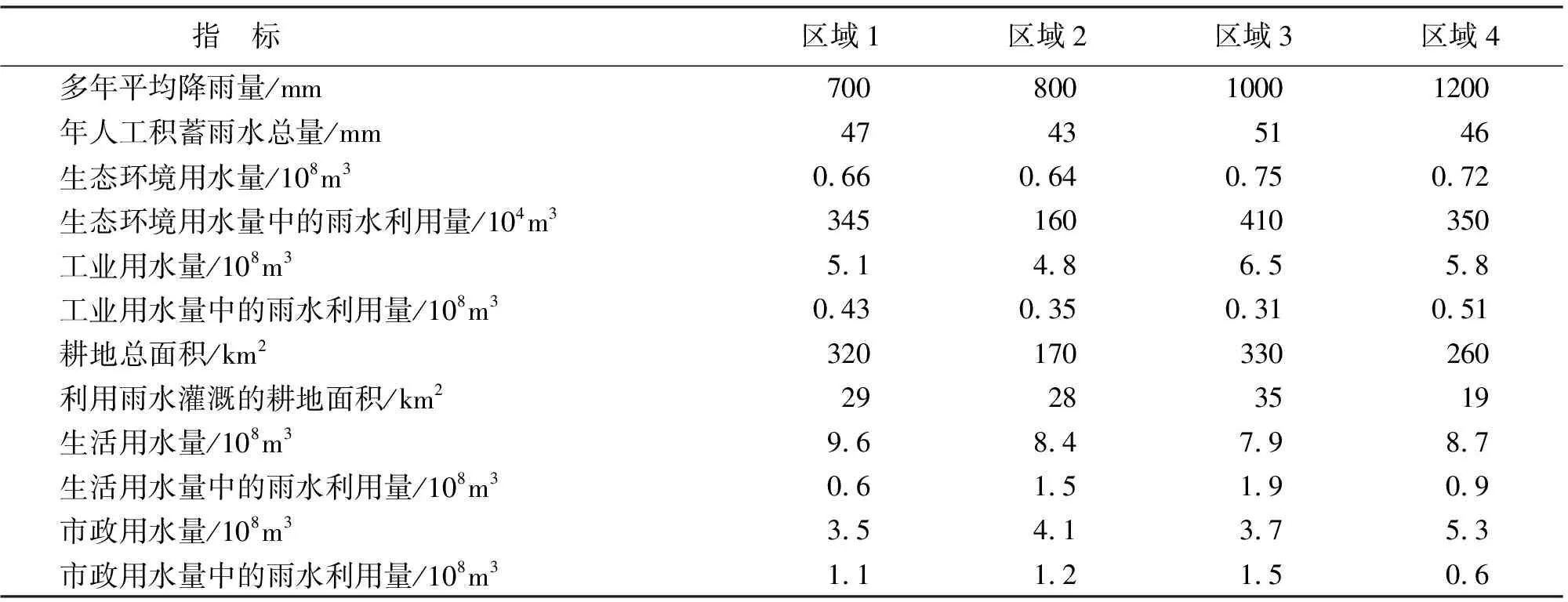
表1 4个区域的雨水利用现状指标表

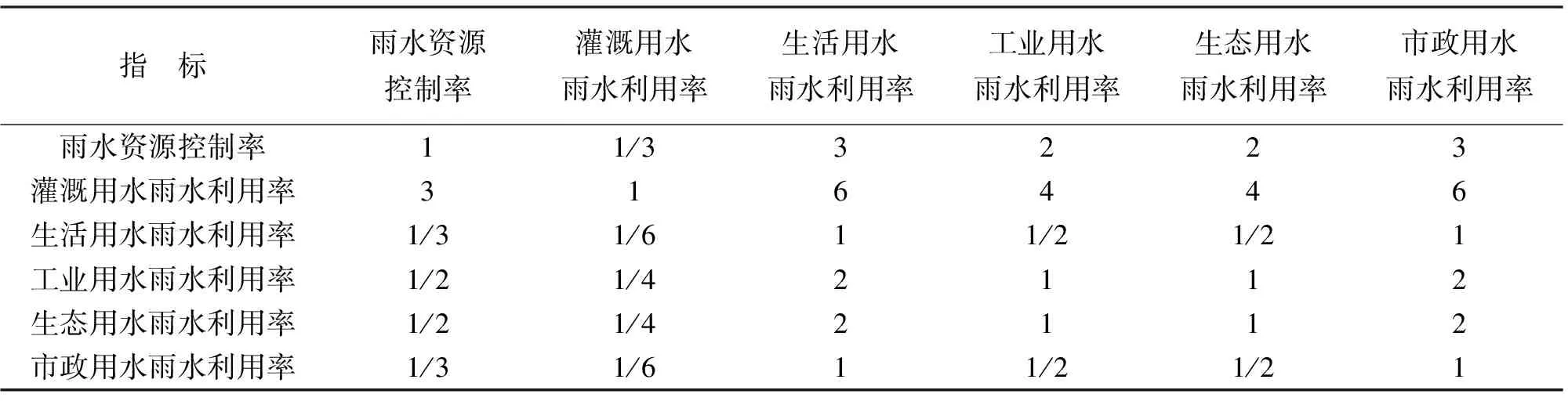
表2 各指标的相对重要性表

根据表2可得判断矩阵A，下面近似地求解λmax和权向量。

计算得到CI为0.0126，RI查表为1.26，则CR=0.0126/1.26=0.01<0.1，所以可认为判断矩阵A满足一致性的要求，所以层次分析法确定的初始权重为(0.19,0.45,0.06,0.12,0.12,0.06)。

根据各项指标的计算公式求出各区域各项指标大小，具体见下表3。

表3 4个区域各项指标值 %

4.2 变权后各评价指标权重的确定

变权分析将层次分析法确定的初始权重与各地区评价指标的值结合分析。由于各个指标之间计量单位、数量级或性质不尽相同，往往使各指标缺乏可比性。

当各指标间的水平相差很大时,如果直接用原始指标值进行分析,就会突出数值较高的指标在综合分析中的作用,相对削弱数值水平较低指标的作用[10]。因此首先需要对各区域的指标值进行无量纲化的处理，本文确定的6个指标皆为“效益型”指标，即越大越好，所以可采用极值化公式(5)进行无量纲化的处理。

(5)

无量纲化处理后的各区域的各指标值参见表4。

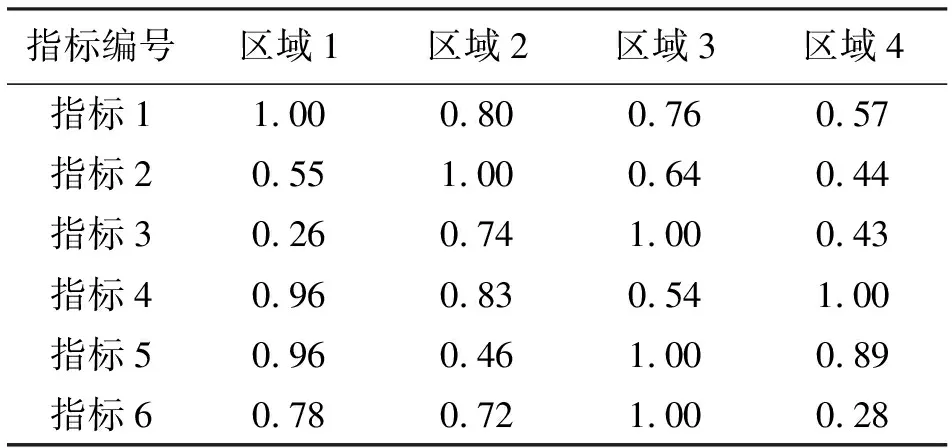
表4 无量纲处理后的4个地区的各项指标值

根据惩罚型变权函数公式对层次分析法确定的初始权重进行变权分析，得到变权后的权重见表5。

从表4可以看出，区域1的指标3的值仅为0.26，远小于其他3个区域，层次分析法确定的指标3的权重只有0.06，变权后的指标3权重则增加到0.15，相应的，区域1较好的指标1、指标4和指标5的权重都有所减小，这样区域1较差的指标3就不容易被其他较好的指标中和掉，保证了综合评价的公平性，同时也体现了本文采用变权分析的必要性。同理可见区域4的指标6。

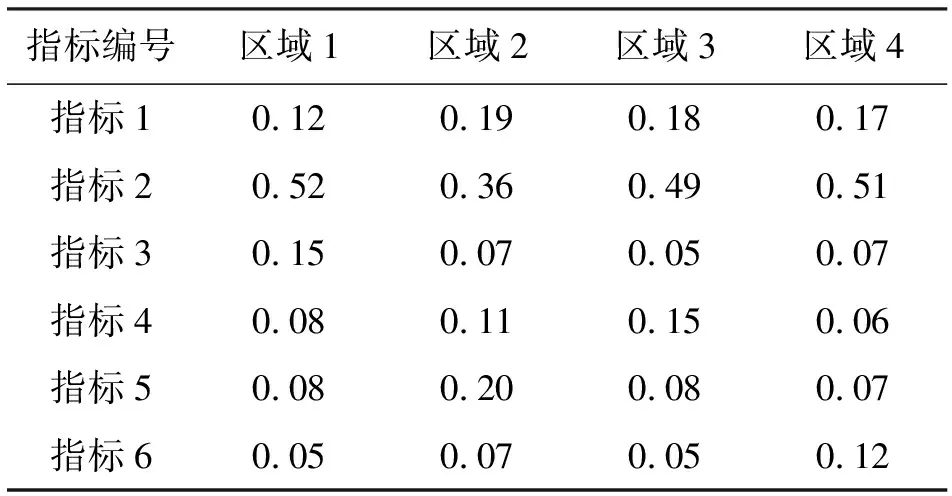
表5 变权后的4个地区的各项指标的权重

4.3 PROMETHEE法运用分析

首先根据优先函数公式计算不同指标下的各地区的相对优先度，具体见表6～11。

计算各区域的相对优先指数、入流和出流，计算结果见表12。

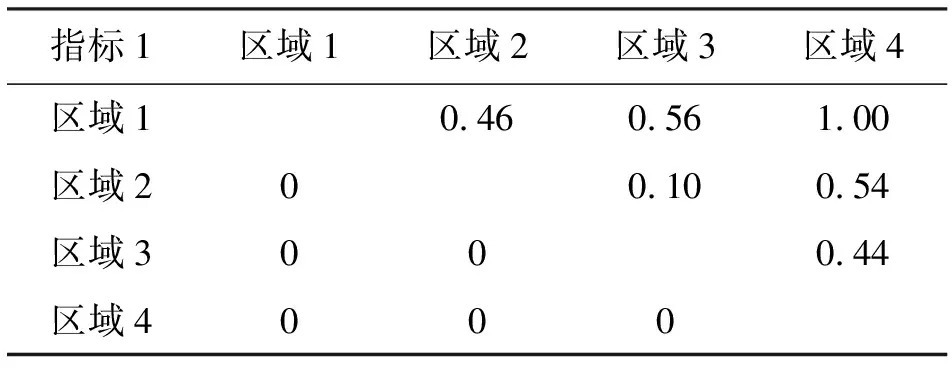
表6 4个地区指标1的相对优先度

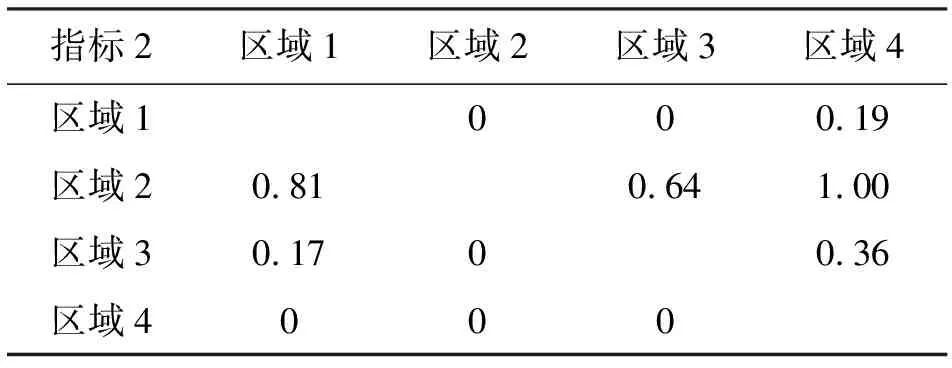
表7 4个地区指标2的相对优先度

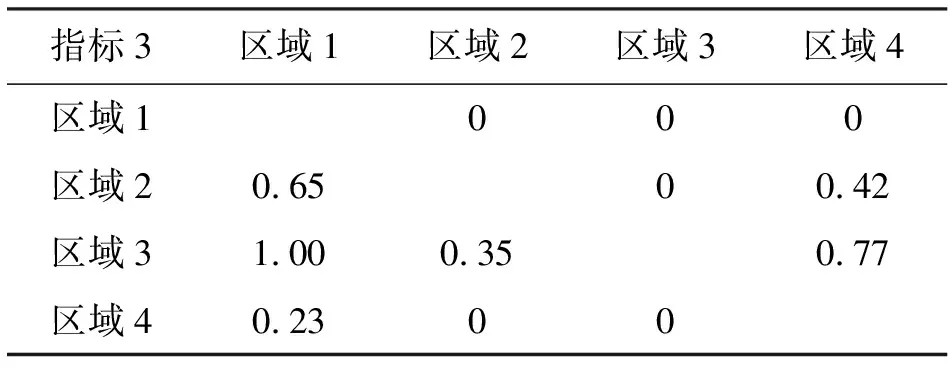
表8 4个地区指标3的相对优先度

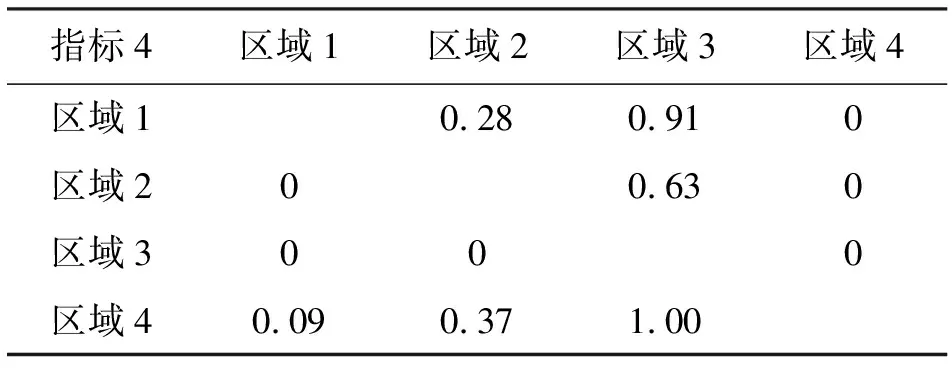
表9 4个地区指标4的相对优先度

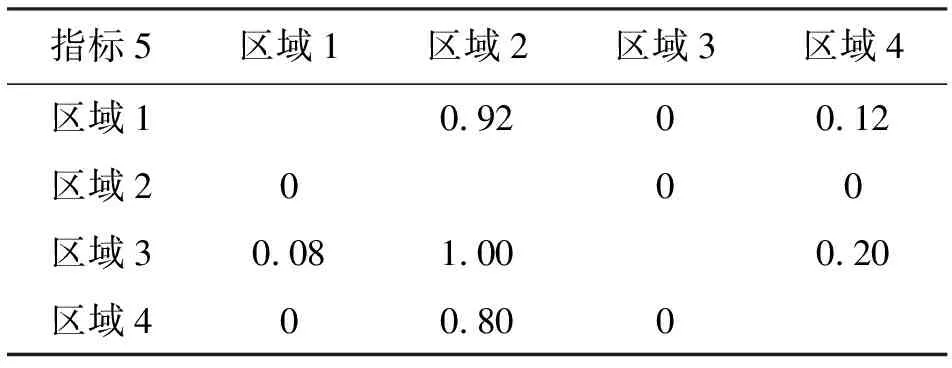
表10 4个地区指标5的相对优先度

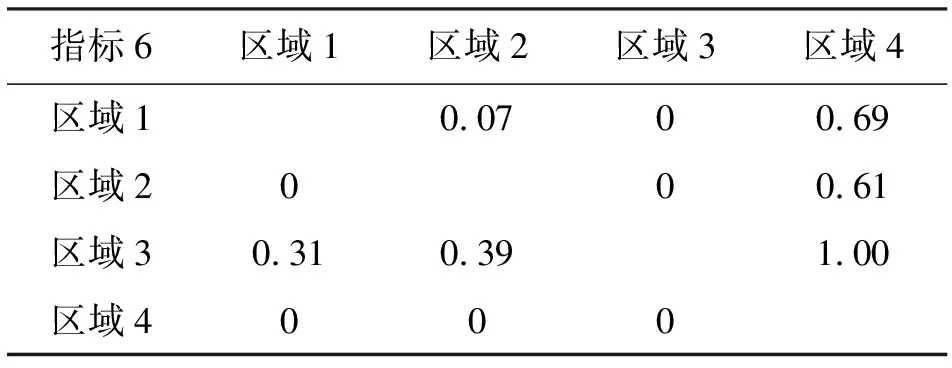
表11 4个地区指标6的相对优先度

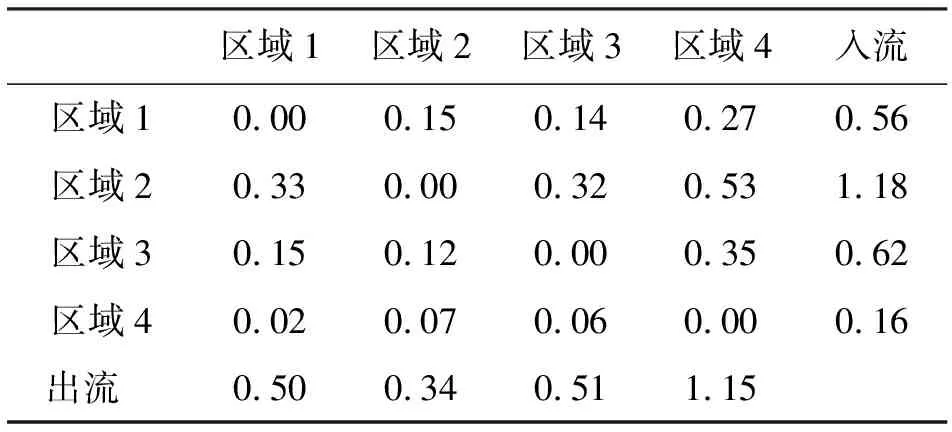
表12 4个区域的相对优先指数、入流和出流

最后按各区域的入流减去出流得出各区域的净流，结果见表13。

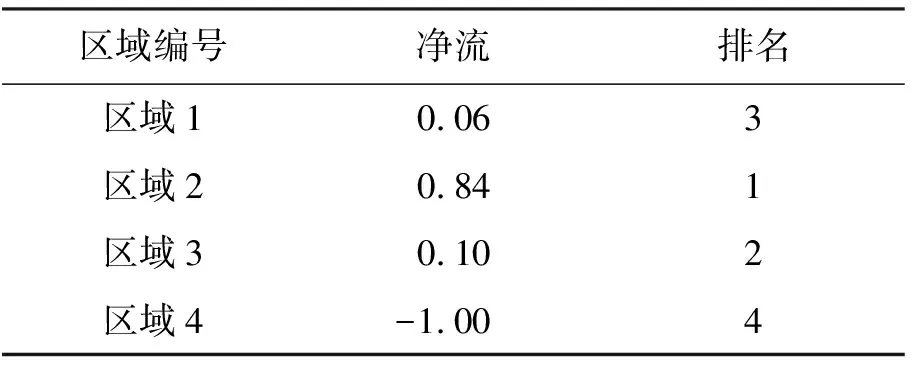
表13 4个区域的净流及排名

根据各区域的净流大小可得4个区域的雨水利用现状的优劣排序，最优的是区域2，且远远优于其他3个区域，区域3和区域1次之，区域4最差，且远远劣于其他3个区域，说明区域4的雨水利用亟待改善。

4.4 可行性的验证

为了验证本文提出的评价模型的可行性，笔者另外采用参考文献[7]提出的综合指数评价法和参考文献[6]提出的模糊综合评价法对本文研究的4个区域进行综合评价，具体结果参见表14和表15。

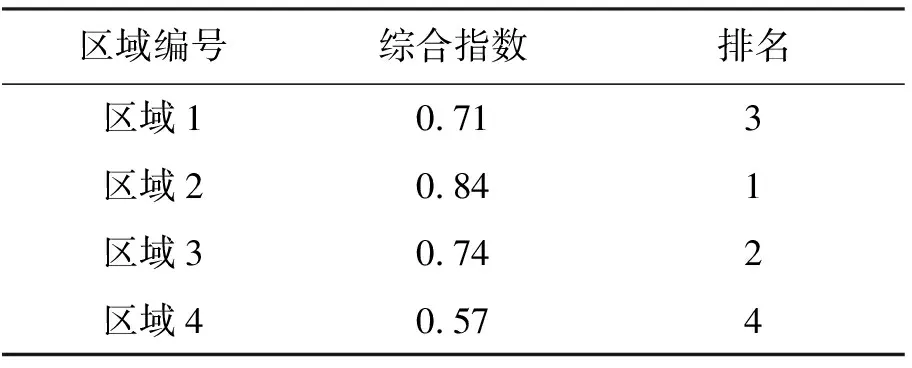
表14 综合指数评价法结果表

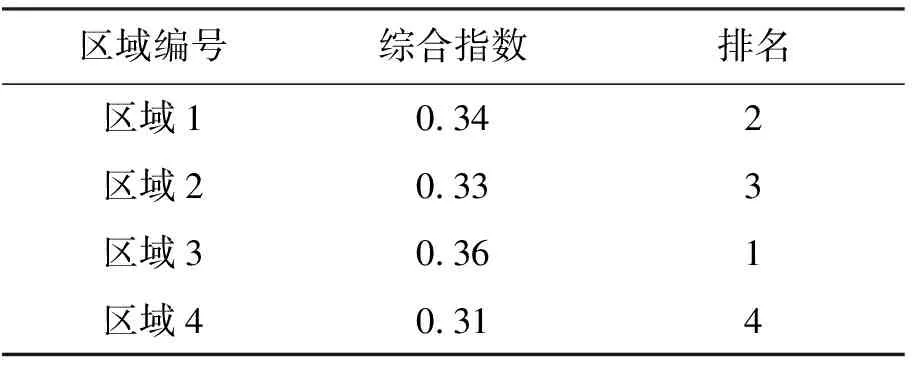
表15 模糊评价法结果表

从表14和15可以看出，本文提出的模型的结果与综合指数法的结果相同。综合指数法适用于评价目的、标准有明确规定，评价对象差异不太悬殊，各单项指标值波动不太大的情况[11]，本文的研究对象比较符合上述要求。而模糊评价法的结果显示，区域3的雨水利用现状最优，区域1和区域2次之，区域4最差，该结果与本文提出的模型的结果以及综合指数法的结果出入较大，而且各地区的评分差距很小，区分度不高。分析模糊评价法的计算过程，在计算隶属度时，并没有对各地区的初始指标值进行预处理，上文也指出，这样会导致突出指标值较大的指标的作用，削弱指标值较小的指标的作用，本文提出的评价模型对初始数据进行了无量纲化处理，保证了评价的合理性。此外，模糊评价法直接采用了层次分析法确定的权重，主观性较大，本文提出的评价模型对层次分析法确定的权重进行变权分析，保证了评价的公平性。

综合3种评价方法，参考文献[7]中的综合指数法简单易懂，但处理过程过于直接，模型会存在误差，并且直接采用了层次分析法确定的权重，不能保证评价的公平性；参考文献[6]中的模糊评价法未对初始指标值进行无量纲化处理，直接采用了层次分析法确定的权重，并且各评价等级以及相应评分的确定的主观性较大，所以评价结果较难满足客观性的要求，而且区分度较差。本文对上述的不足之处进行改进，兼顾了主观性和客观性，区分度较高且结果比较合理。

4.5 针对性改进建议

为了便于给不同区域提出针对性的改进建议，可将各地区的各指标除以相对应的指标权重，得出同一区域下不同指标的评分，具体结果见表16。

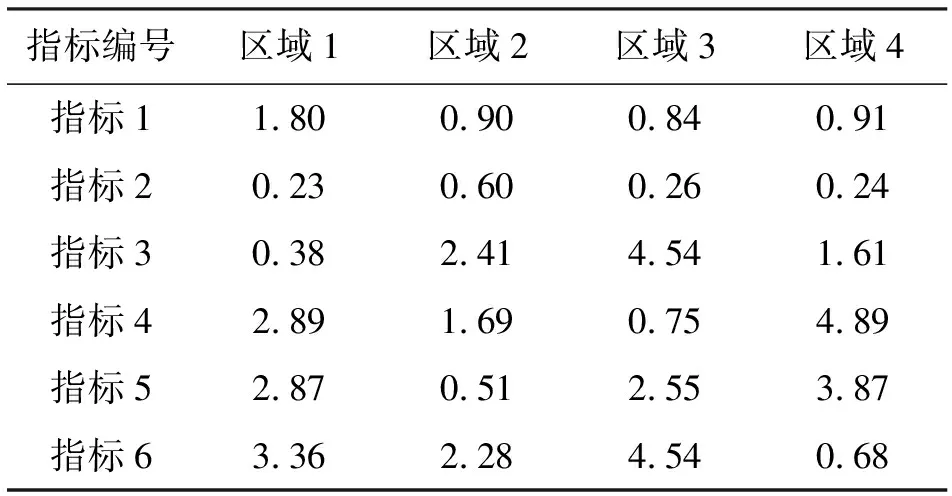
表16 同一区域下的不同指标的评分

从表16可以看出区域1的指标2和指标3评分较低，即农业灌溉用水中雨水所占比例和生活用水中雨水所占比例较低，因此对于区域1来说，这两个指标是需要着重改善的。具体可以修建和完善农业和生活雨水利用工程，改进雨水利用技术。其他地区类似，在此不再赘述。

5 结 论

(1)本文提出的基于层次分析法的变权PROMETHEE模型思路清晰，简单易行，容易被决策者理解和接受，可用于多指标多方案的综合评价，采用该方法对云南省4个区域的雨水利用现状进行评价，结果显示，区域2的雨水利用情况最优，区域4的雨水利用情况最差，同时给出了同一区域的不同指标的评分，以便于不同区域针对性地改进工作。

(2)与现有的评价方法不同，本文采用层次分析法确定初始权重，然后运用变权分析的方法，兼顾了评价的主观性和客观性，同时保证了评价模型的合理性和公平性。

(3)PROMETHEE评价法的优先度的计算与模糊评价法的隶属度的计算相比客观真实，不受评价等级的约束。

综合来看，本文提出的评价模型具有较大的实用性。