循环往复荷载作用下透榫节点模型试验研究

李 溢, 任 青, 程 镇, 崔 宇

(上海理工大学 环境与建筑学院， 上海 200093)

1 研究背景

木结构建筑是人类建筑史上应用时间最久的建筑结构之一，我国传统木结构建筑的一个重要特征是结构构架中的梁柱采用榫卯连接，并且无需一钉一铁。这种特殊的连接方式是将榫头插入卯口中，使得榫头与卯口相互接触。榫卯节点有燕尾榫、馒头榫、透榫等多种类型。在地震作用下，榫卯节点之间反复相对运动，使得梁柱的榫卯连接产生松动，比如在汶川地震中，距离震中约189 km的广元市逍遥楼就遭受到一定程度的破坏，且节点的破坏会导致整体结构发生倾斜甚至倒塌的危险，因此了解榫卯节点的受力性能是古建筑木结构修缮加固保护的基础。

目前，国内外学者都已经对古建筑木结构榫卯节点进行了部分研究。试验研究方面，康家华等[1]通过足尺模型低周反复加载试验研究了整体轻型木结构房屋中底层墙体的破坏模式及抗剪强度、位移、刚度、延性和耗能等力学性能指标。Chun Qing等[2]通过低周反复试验研究了3种不同的榫卯节点，得到了弯矩-转角关系曲线及骨架曲线，最终得出节点的初始弹性刚度。商博渊[3]利用作图法对模拟生物劣化的减榫进行了试验研究，从而得到节点的初始刚度和屈服弯矩。张风亮[4]制作了1∶3.52殿堂木结构模型，并通过模拟地震振动台试验研究了缩尺结构地震反应的变化规律及其动力特性。隋龚等[5]通过节点模型低周反复试验得出了榫卯节点骨架曲线及其弯矩-转角滞回曲线，并拟合得出榫卯节点恢复力模型，比较试验结果提出榫卯连接的刚度非线性关系。姚侃等[6]通过对燕尾榫节点模型的加载试验，研究了燕尾榫节点的半刚性连接性能，推导出榫卯节点的连接刚度，并通过理论拟合出节点的恢复力模型。Seo等[7]通过静力及低周反复加载试验对韩国古建筑中的木结构节点进行了研究，其中梁柱采用燕尾榫节点，木结构中部横梁和柱子为直榫节点，得出静力加载时的荷载-位移曲线及低周反复加载情况下的弯矩-转角滞回曲线，并给出了修正的双目标恢复力模型，且给出了各参数的建议数值。Pang等[8]通过静力加载试验研究梁肩对于韩国传统木结构建筑节点受弯承载力的因素。理论研究方面，谢启芳等[9]、周乾等[10]在分析燕尾榫节点受力机理的基础的前提下，通过力学平衡和变形协调理论推导出了燕尾榫节点的弯矩-转角关系，结合已有的燕尾榫节点拟静力试验结果，研究得出木构架以屈服点、极限点为特征点的弯矩-转角双折线模型并给出了模型特征点的参数计算公式。潘毅等[11]在模型试验的基础上，利用MATLAB编制程序对节点构件进行了静力和动力分析，并且建立了榫卯连接木构架的弯矩-转角关系力学模型。李书进等[12]通过足尺木结构房屋振动台试验研究了房屋在不同地震和烈度下的动力反应和抗震性能，以及结构的破坏形式和破坏机理。吕西林等[13]通过对一个两层、足尺的穿斗式结构房屋模型的榫卯节点附加黏弹性阻尼器进行振动台试验，研究了结构的抗震性能。高大峰等[14]通过对木构架模型在水平反复荷载作用下的试验研究，得到了榫卯节点的转动刚度以及额枋、柱的部分截面的变形和内力特征。

可以看出，现有的研究大部分都是以燕尾榫为主，很少有涉及其他类型的节点。并且大部分试验集中在静力试验的研究，对于榫卯节点的动力试验研究相对较少。基于此，本文按照清《工程做法则例》等文献的构造方法，以古建筑木结构透榫节点为对象，考虑不同循环荷载比即加载幅值、不同频率、不同加载频次的影响，通过长期反复循环荷载试验对透榫节点的动力特性进行研究。

2 试验概况

2.1 模型设计与制作

参照清代《工程做法则例》的做法，选用清式八等材大式建筑的榫卯节点，制作了缩尺比例为1∶5.3的榫卯节点模型，榫卯节点采用抗拉拔能力较好，广泛应用于明清时的透榫节点。节点模型均由古建木工师傅手工制作，并且模型尺寸相同。清式各参数详见表1，模型尺寸详见图1。模型所选用材料为东北落叶松，均为自然干燥半年原木，具体力学性能详见参考文献[15]、表2。

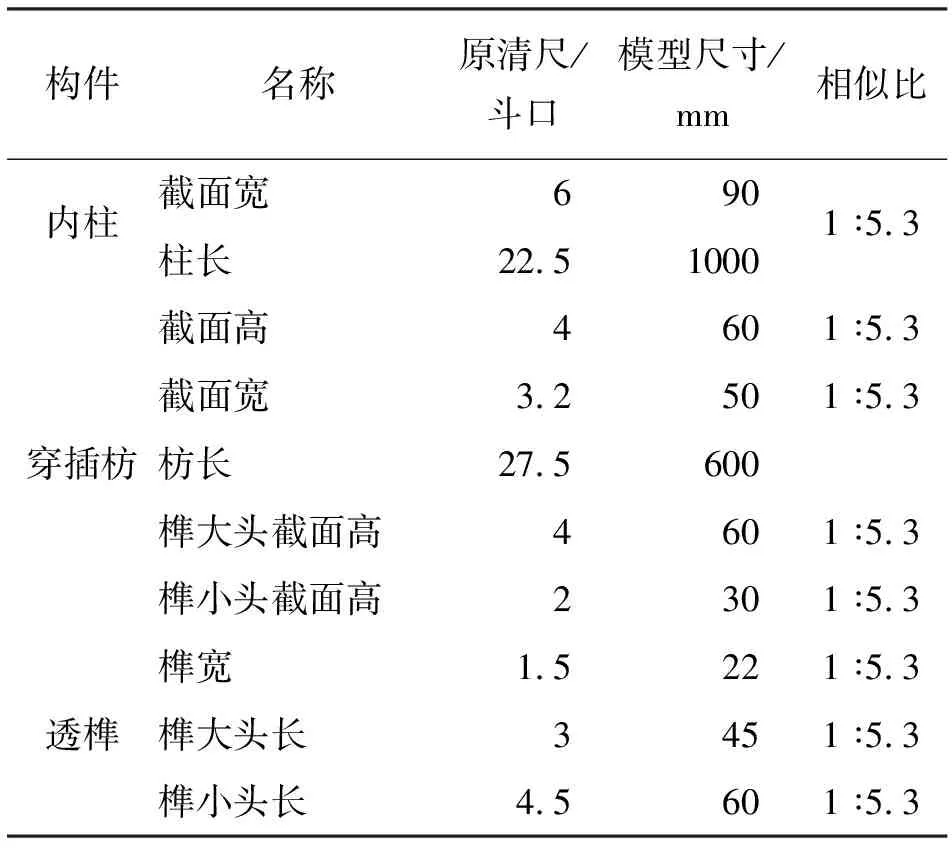
表1 节点模型尺寸

注：斗为清代计量单位，1斗=80 mm，试验研究重点在于节点处，柱长和枋长的确定，仅为加载方便，并未按照原清尺尺寸。

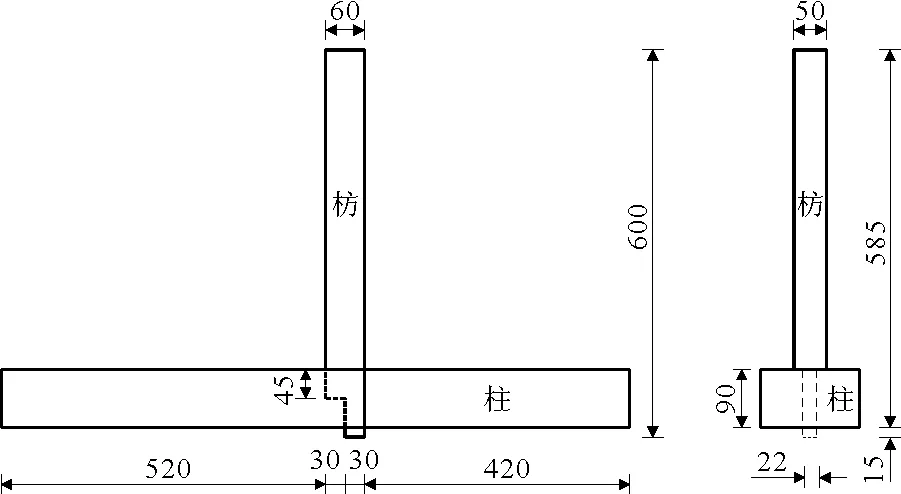
图1 透榫节点构造图(单位：mm)

表2 木材力学性能MPa

2.2 模型试验加载装置

试验主要研究透榫节点的受力性能，因此保持节点处的边界条件与传统古建筑木结构相同，并且为了防止加载过程中由于竖向荷载引起的P-△效应，本次试验中将柱平置，两端固定不动，枋竖向放置，由激振器在枋端部施加水平荷载使得透榫节点产生转动，如图2所示。

图2 试验布置图

试验时将柱两端固定在模型槽的角钢框架上，模型槽尺寸为120 cm×120 cm×150 cm，然后通过柱端千斤顶施加柱所承受的轴向荷载，模型槽结构能够满足加载过程中对强度及刚度的要求，并能有效减小试验中的边界效应。水平荷载由激振器控制加载，水平加载点距离柱上边缘的距离为500 mm。激振器固定在反力墙上，通过前端连接件与枋端部连接。图3为模型试验系统的连接示意图，由反力系统、加载控制、数据采集3个部分组成，试验过程中主要使用的元器件有应变片、激光位移传感器、动态应变采集仪、力传感器、激振器、功率放大器、反力装置等。功率放大器可以根据实际需要提供以某种规律变化的电压信号，实现各种动荷载的加载控制，榫卯节点位移自动采集系统由激光位移传感器和动态应变采集仪组成。

2.3 模型试验量测装置

在距离柱边缘高度为500 mm的枋端右侧20 mm处布置一个激光位移传感器(WJ1)，用来测量枋加载点处的水平位移；在枋的左侧同时也布置一个激光位移传感器(WJ2)，用来测量榫头的拔出量。通过电脑USB线连接加载系统从而收集不同输出力类型、大小以及激振频率得到的数据，测点的具体布置见图3。

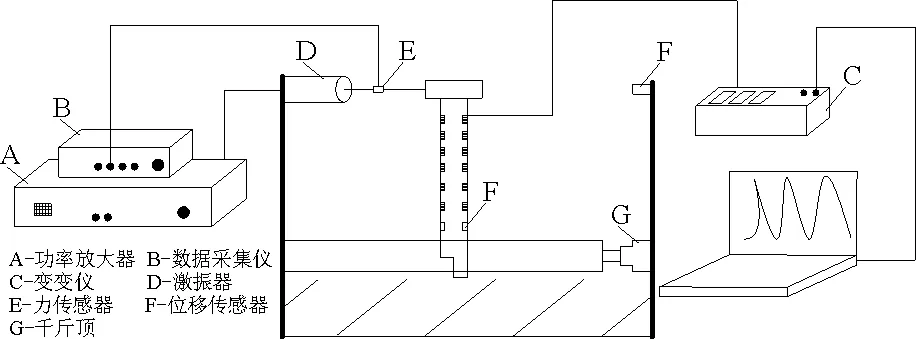
图3 试验装置示意图

3 模型试验方案及参数选取

关于榫卯节点承载力的影响因素很多，理论推导较为困难，因此榫卯节点的抗弯承载力需要通过试验研究获得。根据文献[16]可得，榫卯节点抗弯承载力计算公式为：

(1)

式中:Mu为榫卯节点的极限抗弯承载力;θ为节点的转角。

文中通过静载试验确定透榫节点的极限承载力，静载试验采用千斤顶在榫卯节点的枋端匀速施加荷载直至构件在节点处出吱吱断裂的响声，通过位移传感器测得枋顶位移并得到极限转角，且用力传感器测得对应的加载力，通过计算与试验所得一致，确定透榫节点的极限抗弯承载力。

通过考察长期水平循环荷载对于透榫节点枋端水平位移和节点拔榫量的影响，对比分析不同加载力以及不同加载频率的循环荷载作用下，透榫节点枋端水平位移以及节点拔榫量位移性能的变化，试验分9组进行。首先通过静载试验确定透榫节点的抗弯极限承载力Quk，给出定义水平循环荷载Qc与Quk的比值λ为循环荷载比，即Qc=λQuk，通过变换不同的循环荷载比λ依次进行不同荷载幅值下的循环荷载试验，表3为节点模型试验的方案。

4 试验现象

根据模型试验方案顺次进行不同循环荷载比条件下的循环荷载试验，为了便于描述，规定加载方向以推为正，以拉为负。在试验加载初期阶段，榫头和卯口之间存在的微小缝隙使得节点之间的连接状态相对比较松弛，榫头和卯口之间主要是以摩擦滑移以及缝隙挤紧为主；随着水平循环加载次数的增大，榫卯节点的枋顶水平方向的位移也随之变大，在此过程中节点发出微弱的响声。

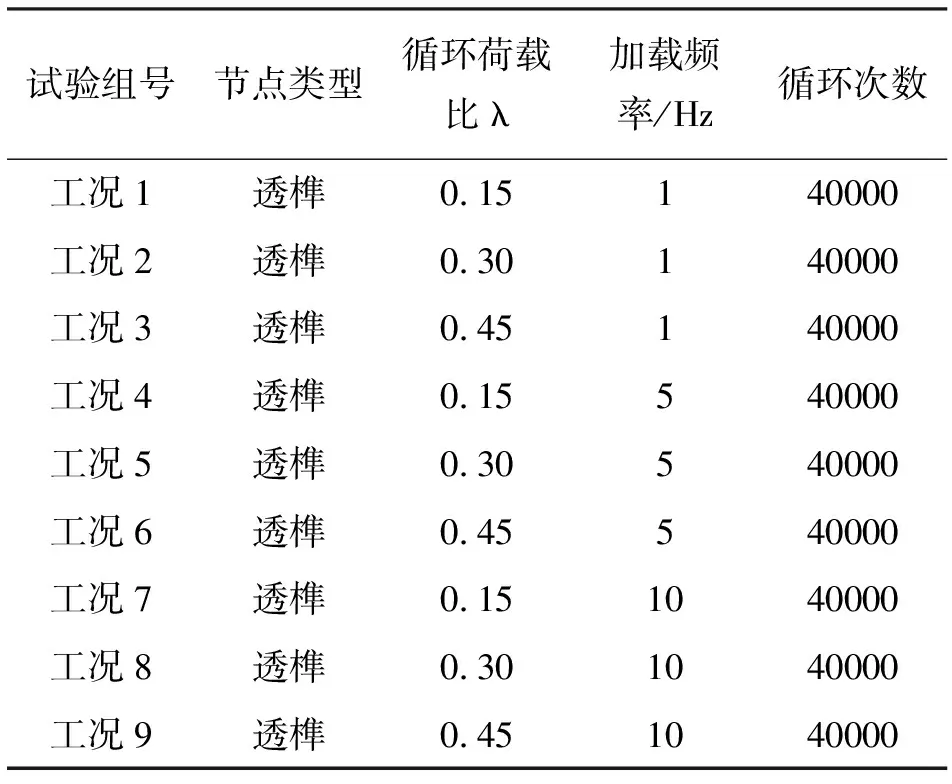
表3 模型试验方案

图4为长期往复荷载作用下枋顶位移及拔榫量的全程曲线变化示意图(工况1)，由图4可知，在单个作用周期内，枋顶位移和拔榫量位移都随着荷载呈现相同趋势的往复变化，当榫卯节点在加载循环后会产生一定程度的残余塑性变形，榫卯节点处的变形组成为弹性变形和塑性变形，枋顶和拔榫量位移会伴随着加载次数增加而增大。Lc为枋顶的位移变化幅值，即一个循环周期内枋顶的位移极大值与位移极小值之差的1/2，同理pc为透榫节点拔榫量位移变化幅值，为一个周期内拔榫量位移最大值和最小值之差的一半，可以看出，作用循环荷载初期，榫卯节点的残余塑性变形大，枋顶及拔榫量的累积位移值发展的速度较快，循环位移幅值相对较小；随着循环次数的不断增加，枋顶和拔榫量累积位移的增加速度会逐渐变小并且趋于相对稳定，但是位移幅值却是有所增大。

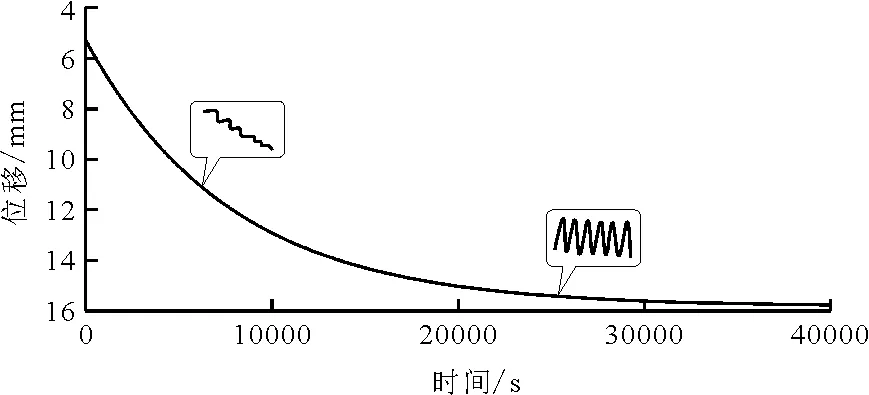
图4 位移时程曲线

5 试验结果及分析

5.1 枋顶位移变化规律

通过激光位移传感器(WJ1)测得透榫节点枋顶在受到水平循环荷载作用下位移的变化，得到了在不同循环加载幅值以及加载频率下作用下透榫节点枋顶位移幅值Lc(mm)与循环次数的关系，并且绘制出节点枋顶水平位移随循环次数N的变化曲线图。图5为不同循环加载频率作用下，λ在不同值时透榫节点枋顶累积位移Lc随着循环次数N的变化曲线图。

从图5(a)中可以看出，当激振频率固定不变为1 Hz，循环荷载比λ=0.15时，20 000次循环后枋顶累积位移达到15.6 mm，累积位移逐渐趋于稳定，不会随循环次数N而无限增加；当λ=0.3时，枋顶累积位移趋于稳定时为20.9 mm，位移幅值相对提高了34%；λ=0.45时，枋顶累积位移经过40 000次循环后为23.06 mm，为循环加载幅值循环荷载比等于0.15时枋顶位移极值的1.5倍。图5(b)、5(c)与图5(a)的变化规律相似，不再赘述。

图6(a)为λ取0.15、0.3、0.45时，10 000次循环加载后枋顶最终累积位移λ-Lc曲线，图6(b)为频率取1、5、10 Hz时，循环加载后枋顶累积位移稳定值f-Lc曲线，可以发现，枋顶位移都随荷载增大而增大，且都是呈现出抛物线形状增长方式，同时在固定加载力的情况下，枋顶位移幅值Lc会随着激振频率的增大而减小。这是由于随着激振频率的增大，榫卯构件结构加速度也随之增大，构件在振动过程中产生的惯性力也越大，反而动荷载作用下透榫节点枋横向运动的弹性力减小。

5.2 节点拔榫量变化规律

定义枋在加载条件下，最外侧枋端边缘的榫头拔出量为节点拔榫量pc(mm)。

图7为在不同加载频率作用下，不同循环荷载比条件下透榫节点拔榫量pc随循环次数变化的规律曲线，水平循环荷载作用下透榫节点拔榫量位移通过激光位移传感器(WJ2)测得，可以发现，在长期水平循环荷载作用下，透榫节点的拔榫量幅值变化较小。当加载频率为1 Hz，λ等于0.15时，10 000次循环后节点拔榫量位移为0.11 mm；λ等于0.45时，节点拔榫量位移最终为0.25 mm为循环荷载比等于0.3时的1.4倍。对比图7(b)、7(c)中均有所体现，且规律同枋顶位移幅值变化相似。

综合上述的模型试验规律可得：循环荷载比较小时透榫节点处发生明显位移变化，当加载频率不变时，透榫节点枋顶位移幅值Lc以及拔榫量pc随着循环荷载比λ的增大而不断变大，并随着激振频率f的增大而减小。

透榫节点在循环荷载初期激振过程中，当循环次数在0～10 000次之间时，节点位移变化幅度比较明显，说明节点残余变形较大，且节点累积位移发展速度较快；随着循环次数的继续增加，节点累积位移的增加速率逐渐减小并趋于稳定，但是最终节点位移幅值却有所增大，这是由于榫卯节点的刚度在加载过程中经历了先逐渐变小后趋于稳定的过程。最后得出循环荷载作用下节点的位移幅值Lc及拔榫量pc与多种因素有关，循环荷载比λ，加载频率f，榫卯节点连接状态等都会对Lc产生影响。

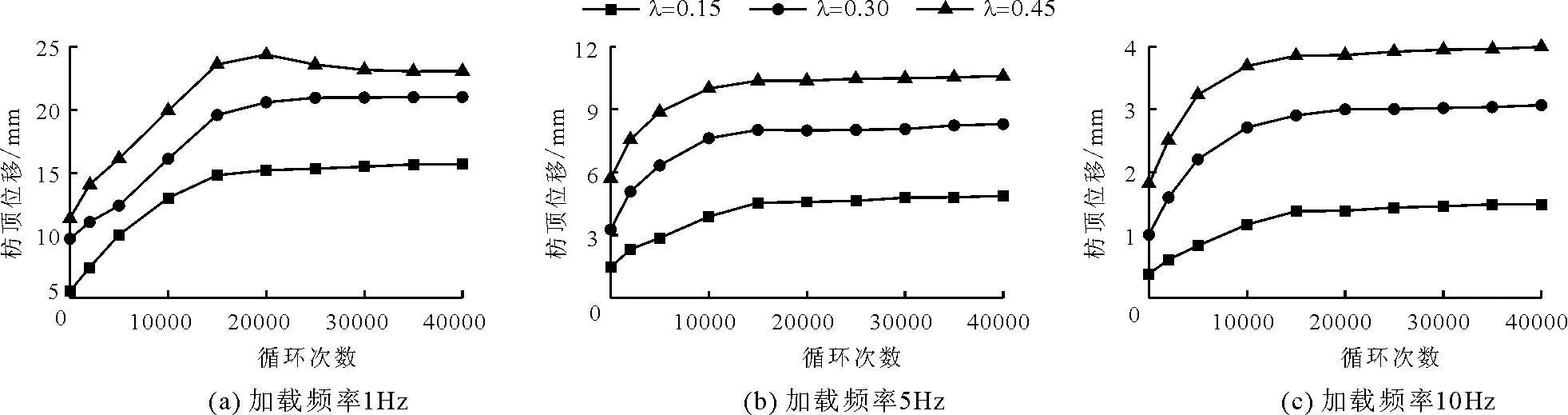
图5 枋顶位移变化规律

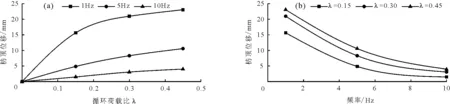
图6 枋顶位移关系曲线

5.3 榫头拔出量与节点转角的关系

节点转角的定义：

(2)

式中：Lc为加载点处水平位移；H为水平加载点至柱表面的距离。

长期循环往复荷载作用下，节点的榫头拔榫量逐渐增大，且节点的刚度在逐渐减小，为了更加直观地了解在长期循环荷载作用下透榫节点的拔榫量与水平转角的变化关系，绘制图8。由图8可知，节点拔榫量均与转角成线性关系，并且随着加载力的增大，节点的拔榫量与转角均会增大。当激振频率增大时，节点的转角和拔榫量均有所减小。

5.4 透榫节点室内试验

目前，对于木结构节点振动的动力特性研究尚有缺乏，在长期循环荷载作用下榫卯节点的位移变化特性研究中对节点破坏形式的认识尚未统一，节点位移的发展规律尚不明确。在现有的木结构设计规范中，通过控制结构的振动位移以及速度来考虑施加荷载的影响，但是当考虑结构的承载力设计时，仍然使用了对于承载力折减的方法进行分析，并未考虑到长期往复荷载作用时榫卯节点产生的位移特性，更无涉及到榫卯节点变化的情况。之前学者研究将不同循环荷载比作用下的结构位移曲线划分为衰减形和破坏形两种类型，本文节点位移曲线为衰减形，对榫卯节点试验数据首先进行归一化处理，然后采用指数衰减函数拟合试验数据，如图9所示。循环位移系数α为加载过程中的节点位移动幅值与节点最终稳定位移幅值之比。

循环荷载作用下，透榫节点的枋顶位移及拔榫量都存在着一个稳定的极大值。随着循环次数的增加，节点位移曲线呈开口向下的抛物线递增趋势，但是其增幅逐渐降低，因此循环荷载周次对节点位移的影响十分显著。当加载频率为1 Hz时，透榫节点枋顶位移幅值与循环周次的关系见公式(3)，拟合结果见表4。

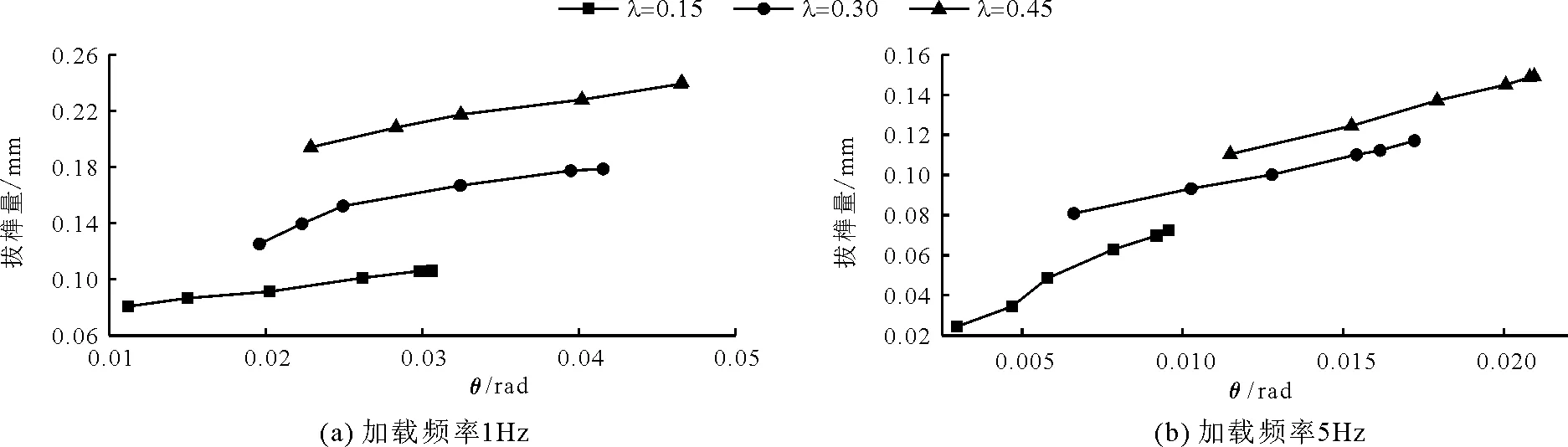
图8 拔榫量与水平转角关系

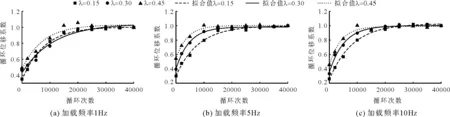
图9 节点位移归一化曲线

y=Aexp(-x/t)+B

(3)

式中：A、B为循环荷载比、加载频率以及节点刚度等有关的系数，A=-0.669～-0.560，B=1.032～1.045。

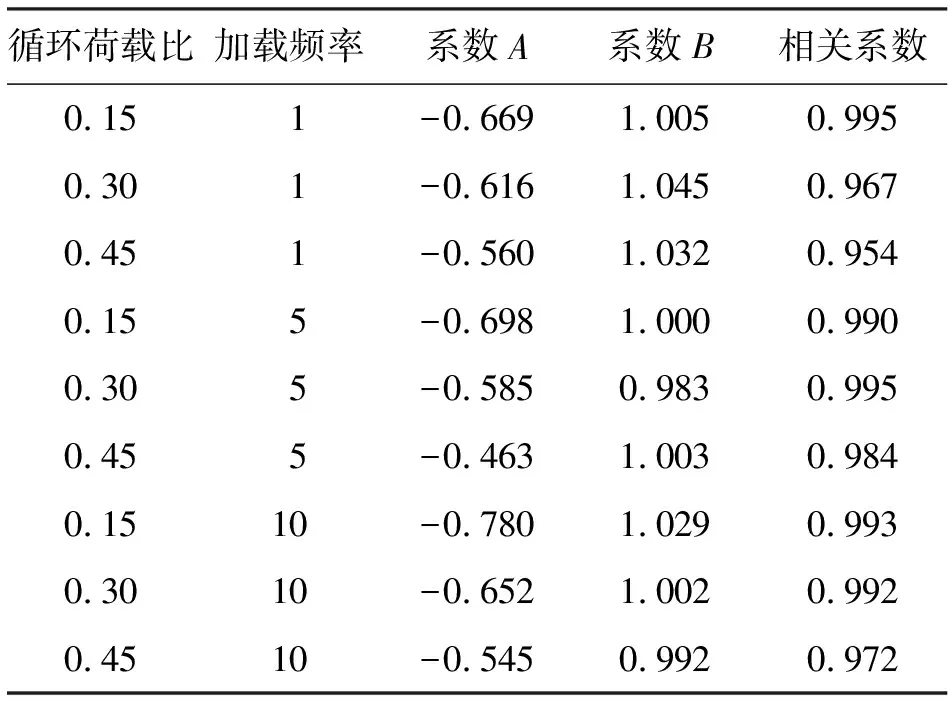
表4 枋顶位移拟合曲线表

6 结 论

通过开展透榫节点模型在水平长期循环荷载作用下的动力特性研究，能够更好地分析古建筑透榫节点结构在受到长期振动荷载、风荷载等循环荷载作用下的安全性能以及稳定性。通过分析数据结构得出如下结论：

(1)循环荷载比较小时透榫节点枋顶即发生明显水平位移变化，当循环荷载加载频率不变时，透榫节点枋顶位移幅值Lc以及拔榫量pc都是随着循环荷载比λ的增大而不断变大。当循环荷载比不变时，节点枋顶位移幅值Lc以及拔榫量pc为随着激振频率f的增大而减小的关系。

(2)透榫节点在循环荷载激振过程中，当循环次数在0～10 000次之间时，枋顶位移幅值Lc变化幅度和拔榫量位移幅值pc变化比较明显，说明节点残余变形较大，且枋顶累积位移发展速度较快。随着循环次数的继续增加，枋顶累积位移的增加速率逐渐减小并趋于稳定，并且最终节点枋顶水平位移幅值却有所增大，这是由于榫卯节点的刚度在加载过程中经历了先逐渐变小后趋于稳定的过程。

(3)循环荷载作用下枋顶的位移幅值Lc以及节点拔榫量位移幅值pc与多种因素有关，循环荷载比λ，加载频率，节点连接状态等都会对节点位移产生影响。榫卯节点的拔榫量与转角成线性关系，最大榫头拔出量随着节点转角的增加而变大。

(4)对长期循环荷载作用下透榫节点室内模型试验的节点枋顶位移曲线进行拟合时，采用指数衰减函数描述枋顶位移和拔榫量随着循环次数的变化规律，其中A，B为与循环荷载比、节点连接状态、加载频率等相关的系数。