基于LIB-SVM的盾构隧道地表沉降预测方法研究
2018-07-21潘宇平耿雪玉
潘宇平, 倪 静, 李 林, 耿雪玉
(1.上海理工大学 环境与建筑学院, 上海 200093; 2.上海隧道股份有限公司, 上海 200082;3.英国华威大学 工程学院, 考文垂 CV4 7AL)
1 研究背景
近年来,盾构法隧道施工技术在全国各大、中城市中应用广泛。盾构隧道多穿越城市中密集的建(构)筑物,使得针对隧道盾构法施工造成的地表变形预测及控制成为工程施工中需要解决的重大技术难题。
国内外众多学者对于盾构隧道施工引起的地层位移进行了广泛深入的研究,主要研究方法包括经验公式法[1-2]、试验法[3-4]、解析法[5-6]、数值模拟法[7-8]等。盾构开挖参数往往随作业环境变化需要进行及时调整及修正,因而在复杂土体环境中经验性的操作往往导致变形的预测计算与实际情况有较大误差。盾构隧道开挖引起地表变形可以看作是一种对地表位移及其影响因素间的复杂非线性函数关系的逼近问题,相比之下,基于统计学理论的机器学习的方法可以高效、准确地预测沉降与盾构掘进的关系[9-10]。孙钧等[11]、Ocak等[12]基于经验选取现场盾构施工相关参数,运用人工神经网络及支持向量机方法(Support Vector Machine)预测地表最终沉降,验证了机器学习方法在岩土工程领域的适用性。Mohammadi等[13]对比了多种盾构开挖参数组合下的神经网络预测模型,根据预测结果的准确性得出土的沉降与容重无关。张俊等[14]对三峡白水河滑坡进行研究,使用时间序列支持向量机方法对滑坡位移成功回归预测。
相较于传统研究方法,机器学习方法避免了繁琐的公式推导及苛刻的试验环境要求,在获取可靠的监测大数据前提下,更为经济、高效地对复杂非线性问题进行回归分析及预测。上述研究表明,机器学习方法适用于岩土工程领域。鉴于此,本文将SVM法应用于研究隧道掘进引起的地表沉降问题中,基于交叉验证参数寻优方法建立LIB-SVM模型,从而准确、高效预测地表变形,以期对隧道施工提供参考。
2 数据与模型
2.1 工程概况
上海市虹梅南路越江隧道于2015年12月30日贯通,连接上海闵行与奉贤两区,全长5.26 km。其中,主线隧道长度3.39 km,是目前黄浦江底最长、埋深最大的隧道,最大埋深达59 m,也是当前国内最深的城市越江隧道。西线隧道全长3391.49 m,东线隧道全长3388.55 m。采用直径14.93 m的超大直径盾构施工掘进,以保证主线双向6车道的通行能力。工程场地主要由饱和黏性土、粉性黏土及砂性土组成,各土层参数如表1所示。
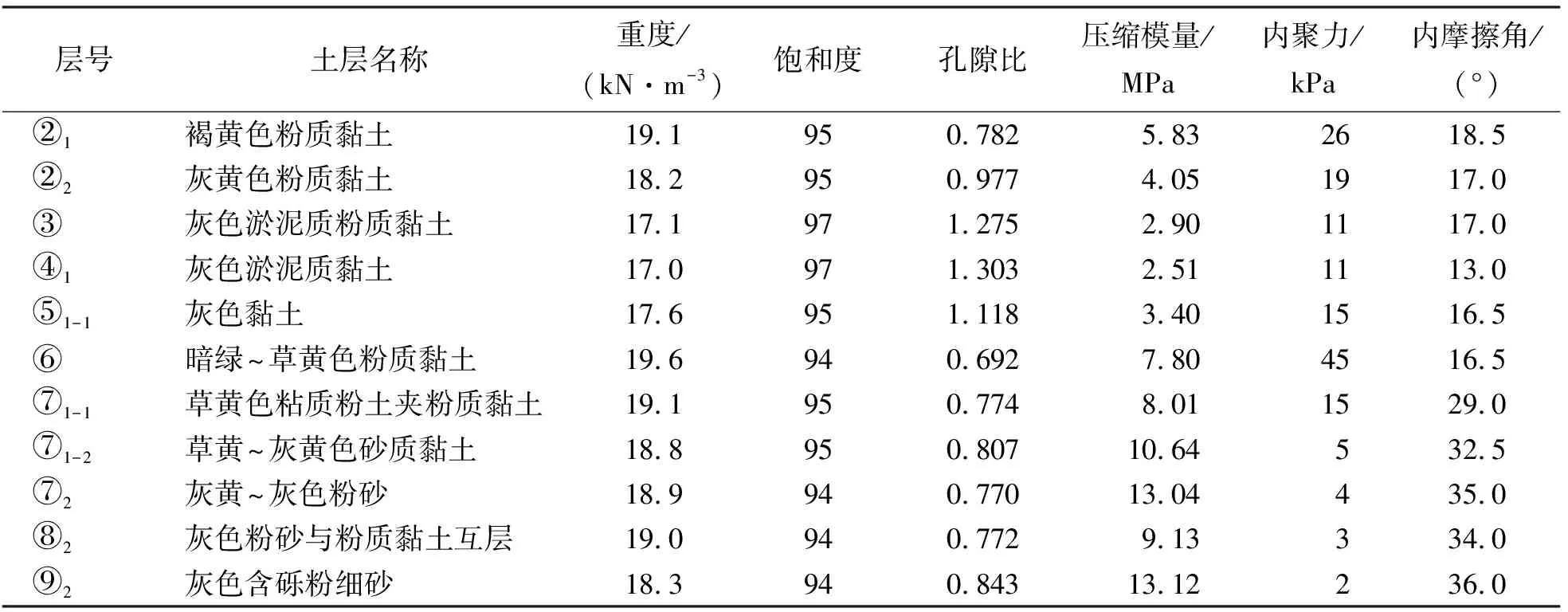
表1 虹梅南路隧道工程穿越地层情况一览表
2.2 SVM模型概述
SVM可以有效地解决分类或回归问题[15]。本文针对盾构隧道开挖引起地表变形的回归预测问题,建立以径向基函数(Radial basis function)作为核函数的SVM模型,将无法线性拟合的样本点(xi,yi),(i=1,…,l)通过非线性变换O(x)映射到高维特征空间[16],并在高维空间内搭建线性模型f(x,k)=(k·O(x))+b,再经过回归返回原始空间中。SVM回归机为:
(1)
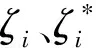
对于式(1),化简为对拉格朗日对偶函数进行优化:
(2)
式中:K(xi,xj)为核函数,K(xi,xj)=(φ(xi)φ(xj))[17]。
2.3 数据采集和特征工程
(1)所用数据是上海虹梅南路隧道西线闵行段的实测沉降原始数据(W480-W1690),整理和选取其中的前125个数据点用于建立模型,后7个数据用于预测,如图1所示。
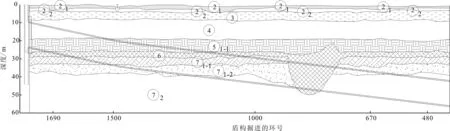
图1 土层剖面及实测点位置图
(2)选取盾构施工引起地表最终地表沉降的主要相关因素,即特征项共8项,包括土层的黏聚力、内摩擦角、压缩模量、盾构掘进速度、盾构掘进时推力、注浆压力、管线流量偏差和隧道埋深,输出为盾构施工引起的地表最终沉降,建立8个输入特征和1个输出目标值的模型。
(3)LIB-SVM要求把每1个样本的特征按照一定的数据格式表示为1个实数行向量:
其中label是训练数据的实测值,本文中的物理意义是最终沉降量(正值代表地表最终隆起,负值代表地表最终沉降),value表示用来训练或者预测的数据,即自变量或特征值。例如:-4.66、5.6、30、16.5、35、45681 …
(4)为了加快收敛速度和避免输入向量中各特征数量级相差过大影响训练效果,调用mapminmax函数对训练数据和测试数据进行归一化处理,输出最终沉降量的归一化区间设为[0,1],输入特征的归一化区间设为[0,1]。
mapminmax函数数学表达为[18]:
(3)
式中:x、y分别为归一化前和归一化后的值;xmin、xmax分别为样本中的最小值和最大值。
2.4 建立SVM模型
支持向量机进行回归分析,需要解决参数和核函数的选择的问题。本文通过对LIB-SVM工具包中的参数择优方法和核函数进行对比分析,找到最适合本研究领域的模型。
选取均方误差(MSE)和相关系数(R)作为评价模型的指标[19]:
(4)
R=
(5)
式中:f(xi)为第i组的预测值;yi为第i组实测值或真实值。
2.4.1 模型参数对(c,g)的选取 采用交叉验证法(Cross-validation)找出一组最佳的(c,g),选择3折交叉验证检验参数,搜索结果见表2,等高线图见图2。

表2 参数对(c,g)的选取
2.4.2 不敏感系数ε的确定 采用上一步所得的最佳参数对(c,g),通过不断变换参数ε的取值对训练数据进行训练,从中选取最优的参数ε,详见表3,同时输出MSE与R。
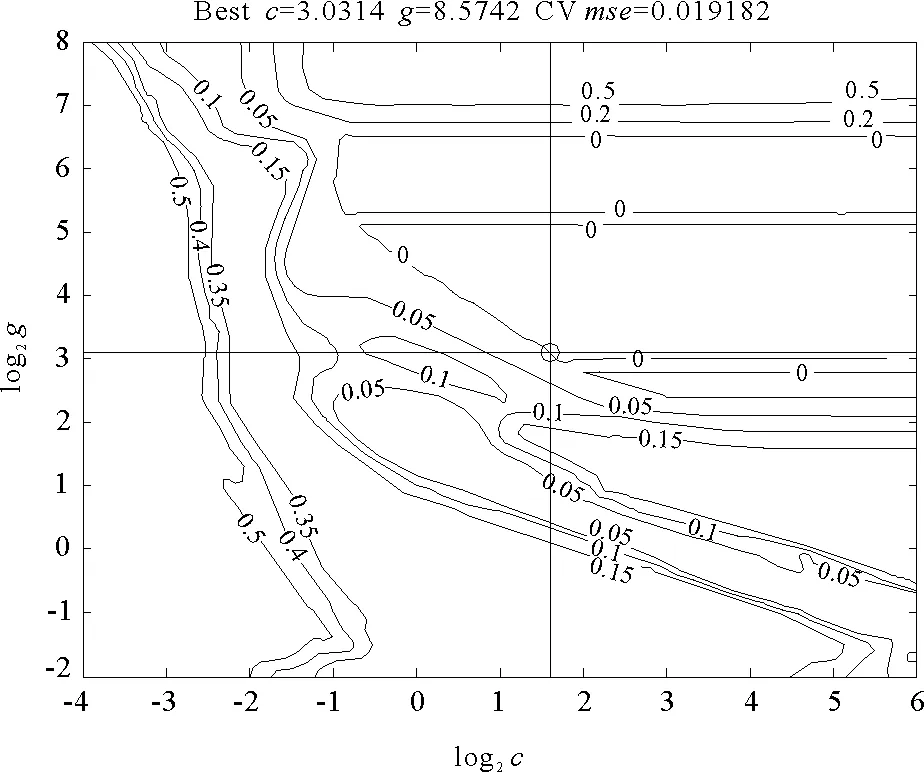
图2 模型参数的寻优等高线图
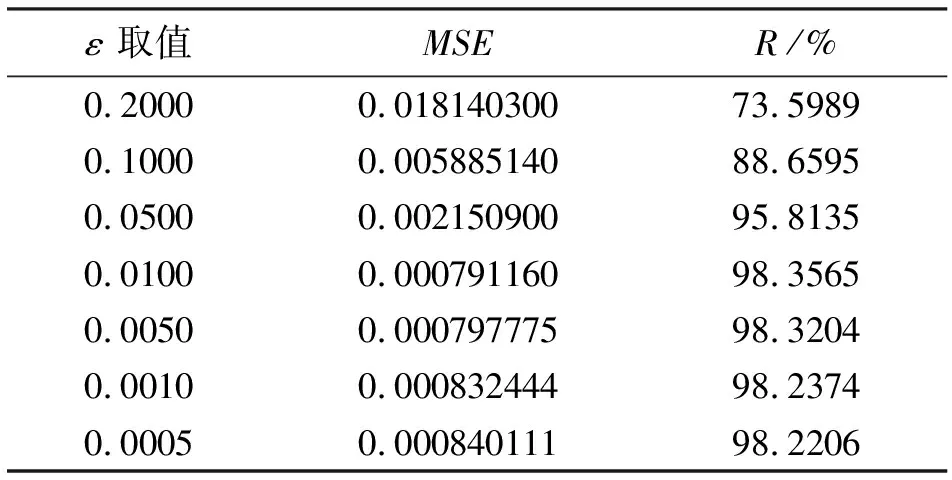
ε 取值MSER/%0.20000.01814030073.59890.10000.00588514088.65950.05000.00215090095.81350.01000.00079116098.35650.00500.00079777598.32040.00100.00083244498.23740.00050.00084011198.2206
由表3可见,当固定c=3.0314,g=8.5742时,控制参数ε取值逐步减小,则相关系数R表现为先增大后减小的趋势。当ε值选择较大时,较少的支持向量参与回归,模型过于简单可能会造成欠拟合;当ε值选择较小时,更多的支持向量参与到回归中,模型过于复杂可能会造成过拟合现象。在本实例中,Cross-validation当参数ε取0.01时,平方相关系数R为98.3565%,得到均方误差MSE最小值,此时拟合效果达到相对最佳。因此,选择ε=0.01。
2.4.3 核函数选取 对常规的SVM核函数进行回归比较,最终发现RBF核函数的回归效果最为理想,如表4所示。
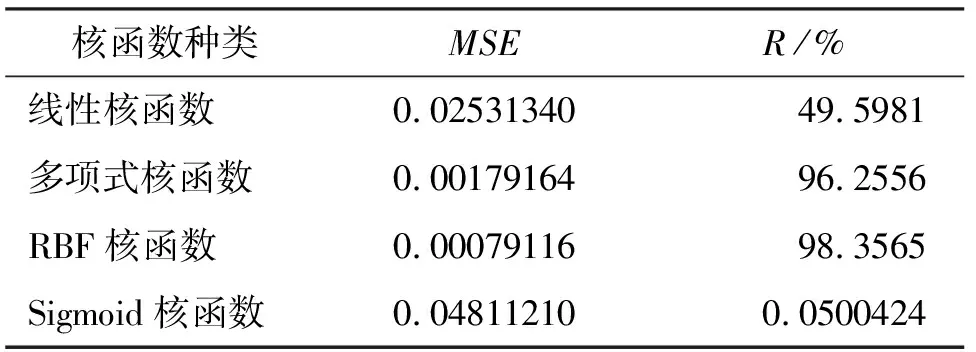
表4 核函数选取
在上述的支持向量机模型中,LIB-SVM类型选择为ε-SVR,选择RBF为核函数,结合通过寻优得到的参数c=3.0314、g=8.5742、ε=0.01。
3 计算结果与分析
3.1 回归结果分析
由前125组训练集数据建立的模型对该训练集数据进行回归预测,得到的实测地表沉降数据与回归预测结果对比见图3。
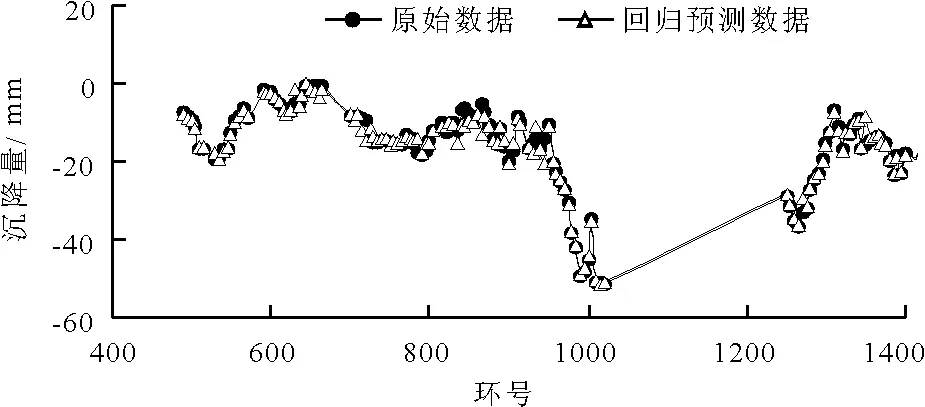
图3 实测地表沉降数据与回归预测结果对比图
由图3可知,支持向量机的训练回归效果较好。两个拟合指标分别为MSE= 0.00079116和R= 98.3565%,说明LIB-SVM支持向量机具有较好的函数逼近能力,对125组训练集数据成功拟合,预测模型建立完毕。
3.2 预测结果分析
由前125组训练集数据建立模型,对接下来的7组测试集数据进行预测,得到的地表沉降实测值与预测值对比结果如表5及图4所示。由表5可知,预测值与实测值的最小、最大相对误差分别为0.5% 和5.6%,误差基本控制在5%以内,预测结果在合理范围内,满足工程实际要求。
支持向量机模型总结过往信息中包含的规律,进而对未来的情况做出预测,这就使得机器学习方法能够利用不断更新的数据进行模型校准,即随着工程进展及数据库的扩容,LIB-SVM模型的预测精度基范围也会逐渐提高。
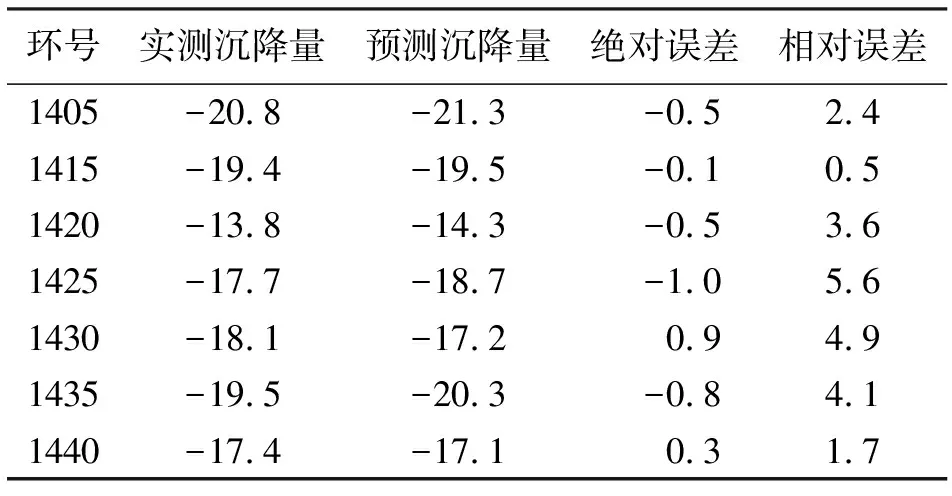
表5 地表沉降实测值与预测值对比 mm,%
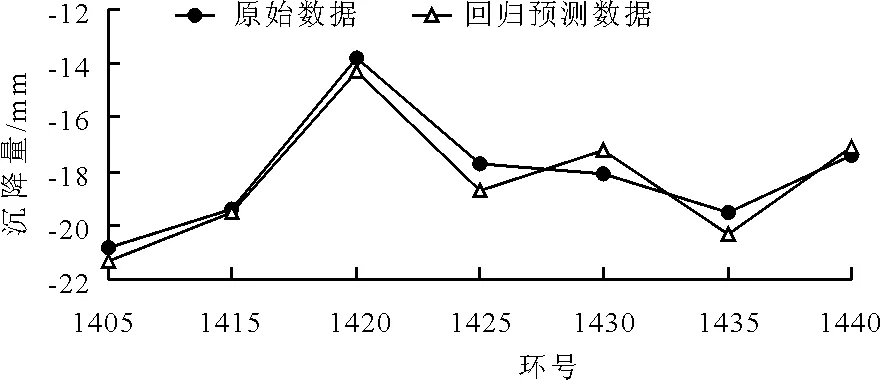
图4 实测地表沉降数据与预测对比图
4 结 论
本文结合虹梅南路隧道西线工程,通过核函数类型选择及模型参数的对比寻优,成功将LIB-SVM方法运用于隧道盾构掘进与最终地表沉降的相关性研究中,并得到与实际监测数据较为一致的结果。根据研究得出结论:
(1)采用LIB-SVM软件包对工程实测数据进行建模和预测,可以把误差控制在相对较小风险内;
(2)对于存在较大误差的训练参数进行合理的降噪处理,以至于个别噪点不会影响建模精确度,增强了模型抵抗干扰的能力;
(3)对于模型学习样本采用特征工程进行数据预处理,不仅可以快速推进LIB-SVM的学习速度,还可以避免LIB-SVM学习的扭曲;
(4)训练完成的LIB-SVM模型,输入地表沉降的影响因素,能相对准确地输出对应掘进断面的最大地表沉降。随着工程推进,数据量与范围的提升,训练的样本得到不断完善,模型的泛化性与预测准确性也会不断提升;
(5)依据虹梅南路隧道西线工程进行建模与预测,结果与实测值吻合较好。表明机器学习可以应用于隧道盾构施工引起地表沉降的预测及预警中,在隧道工程领域有着一定的发展前景。
