基于MAGA-PPC模型的水资源配置方案综合评价
2018-07-21王庆杰岳春芳李艺珍
王庆杰, 岳春芳, 李艺珍
(新疆农业大学 水利与土木工程学院, 新疆 乌鲁木齐 830052)
1 研究背景
随着工、农业的发展和城市化进程的加快,水资源短缺、水资源利用率低、水生态环境恶化等一系列水问题已制约着我国经济社会的可持续发展[1],水资源合理配置是解决这些问题的有效途径之一。区域水资源配置涉及经济、社会、资源、生态等多方面的内容,现有的水资源配置模型虽然能够考虑多方面的因素,但由于配置的多目标性导致模型优化出的可行性方案较多,管理者在方案决策时难以做出判断,水资源配置评价可为方案决策提供技术支持。
常用的水资源配置评价方法有TOPSIS法[2]、模糊物元分析法[3]、D-S证据理论[4]、格序理论[5]、模糊熵模型[6]、灰色聚类模型[7]、概率神经网络模型[8]等,这些方法各具特色,如前6种方法属于半定量研究方法,需权重参与评价,而权重确定的合理性直接影响方案评价的结果,神经网络法需要较多专业知识和经验对构造的网络模型进行训练和学习,主成分分析法建模时必须判定多种现象和确定多个合理参数,而且需要大量的样本参与评价。
Friedman等[9]于1974年提出处理高维、非线性、非正态数据特点的投影寻踪聚类(PPC)技术,1986年李国英[10]将其引入国内,自2000年被张欣莉等[11]在水质评价中首次应用后,PPC评价模型能够有效解决方案优劣评价、等级划分、指标性质探索及重要性排序等问题。多智能体遗传算法(MAGA)是将人工智能中的多智能体引入到遗传算法中而成的一种混合进化算法,在超高维函数优化、线性系统逼近、多目标优化等领域已经取得了较好的应用效果[12]。在水资源配置方案评价中尝试使用MAGA进行PPC建模,旨在提高水资源配置评价结果的可靠性,为水资源管理决策分析提供新的方法。
2 构建水资源配置方案评价模型
2.1 样本数据预处理
为了避免评价指标间的量纲影响,按以下公式进行标准化处理[13]:
效益型指标:
(1)
成本型指标:
(2)
区间型指标为:
(3)
式中:xj max、xj min分别为第j评价指标中的最大值、最小值;[S1,S2]为第j指标的最佳区间。
2.2 聚类分析
设投影方向为aj(j=1,2,…,m),则第i个样本的一维投影特征值为:
(4)
通过最大化投影值Zi的标准差s(a)和类内密度d(a)来寻找最优投影方向[14-15],投影指标函数表达式Q(a)见公式(5),最优投影方向的实现见公式(6)。
Q(a)=s(a)d(a)
(5)
(6)
s(a)和d(a)的计算见公式(7),其中rik为两方案投影值间的距离rik=|Zi-Zk|,u(R-rik)为单位阶跃函数,当R>rik时,u(R-rik)=1,否则u(R-rik)=0,密度窗宽R的取值以楼文高[16]推荐的取max(rik)/5≤R≤max(rik)/3为标准。
(7)
2.3 寻找最优投影方向
采用多智能体遗传算法(MAGA)[17-18],用投影方向向量进行编码,将每一个投影方向视为一个智能体储存于一个L×L的网格环境中。程序初始化时,赋予所有智能体等于投影指标值相反的能量;程序运行时,互为邻域的智能体间通过竞争、高斯变异、自我学习的方式增加能量实现进化。计算过程如下:
设Lt为第t代智能体网格,Lt+1/3、Lt+2/3为Lt和Lt+1间的中间代智能体网格;Bestt为L0、L1、…、Lt中的最优智能体;Cbestt为Lt中的最优智能体;Energy(Lt)是智能体的能量;Pc、Pm为预先设定的参数,分别控制领域正交交叉算子和高斯变异算子的执行;U(0,1)为0~1间均匀分布的随机数。
步骤1:初始化参数和智能体网格L0,计算每个智能体的能量,找出能量最大的智能体Cbest0,令t=0开始迭代循环。
步骤2:对每个智能体执行领域竞争算子,得到新的智能体网格Lt+1/3。
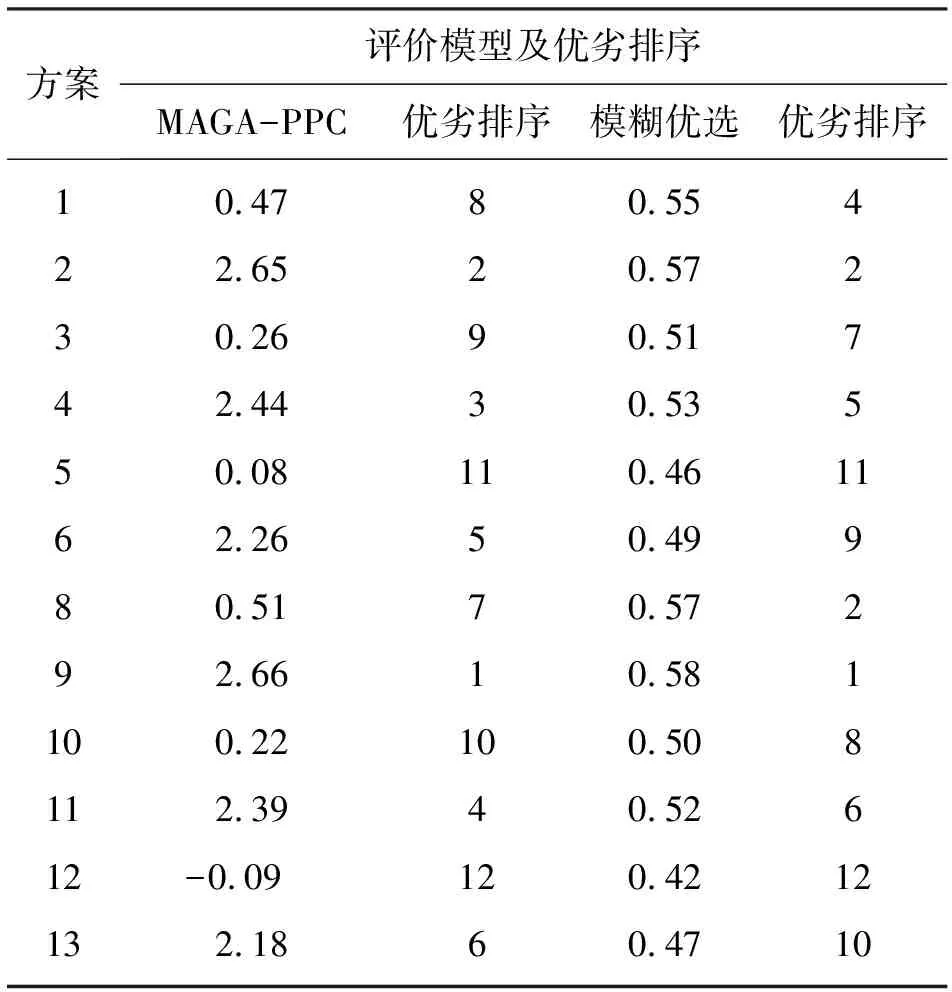
步骤3:若U(0,1) 步骤4:若U(0,1) 步骤5:从Lt+1找出Cbestt执行自学习算子。 步骤6:若Energy(Cbestt)>Energy(Bestt-1),则令Bestt=Cbestt,否则Bestt=Bestt-1。 步骤7:判断进化代数是否达到最大迭代次数N,若是,输出Bestt,否则,t=t+1并转步骤2。 步骤8:根据Bestt投影指标函数,输出模型运算结果。 渭河发源于甘肃渭源县鸟鼠山,流经甘肃、宁夏、陕西3省,流域总面积13.5×104km2,兴水治旱是渭河流域治理的主题。这里借鉴文献[19]中的成果,以陕西省引汉济渭受水区5座大城市、13座小城市和8个工业园区的水资源配置研究为例,从水资源的需求侧、供给侧、模型侧3个方面入手设置13个水资源配置方案,详见表1。 根据水资源供需平衡分析,方案7缺水较为严重不纳入评价。考虑水资源管理的相关政策以及受水区水资源开发利用的现状,从社会、经济、生态和资源4个方面构建水资源配置评价指标体系见表2,根据表2中指标的计算方法,确定各方案的具体评价指标值见表3。 首先建立MAGA-PPC水资源配置方案评价模型,模型中智能体网格大小L取为30,最大迭代次数N=200,竞争概率Po=0.2,交叉概率Pc=0.1,变异概率Pm=0.1,密度窗宽R=rmax/3。 采用公式(1)~(3)标准化处理表3中的方案评价指标,根据研究区的现状特点,水资源开发利用率取[0.45,0.5]为最优区间,标准化值见表6。 经MAGA-PPC模型计算,目标函数值Q(a)= 1762.7,投影窗宽半径R= 0.9209,最优投影方向a=(0.0015,0.1496,0.1535,0.4222,0.4253,-0.1279,0.4268,0.1275,0.1251,-0.0334,0.426,0.4262)。根据MAGA-PPC模型计算得出的评价结果,将其与文献[19]的评价结果进行对比,结果见表7。 表1 2020年陕西省引汉济渭受水区水资源配置方案集设置 注:“√”表示采取的措施。 表2 2020年陕西省引汉济渭受水区水资源配置方案评价指标体系 注“∧”表示效益型指标,“∨”表示成本型指标。 表3 2020年陕西省引汉济渭受水区水资源配置方案评价指标值 表4 模型验证指标 表5 模型验证时的最优投影方向向量 表6 2020年陕西省引汉济渭受水区水资源配置方案评价指标准化值 表7 2020年陕西省内引汉济渭受水区水资源配置方案评价结果 对综合评价结果进行分析,得出结论如下: (1)方案可划分为两个等级,即方案9、2、4、11、6、13的水资源配置情况较优,为等级Ⅰ;方案8、1、3、10、5、12的水资源配置情况一般,为等级Ⅱ。由表1可知:等级Ⅰ中的方案均采取了强化节水措施,等级Ⅱ中的方案均未采取强化节水措施;同等级中的方案,调水量越多,方案越优;等级Ⅰ和等级Ⅱ中,在调水和其他配置措施相同的情况下,选用优化模型与模拟模型的两个方案评价结果相近,即方案1和方案8、方案2和方案9、方案3和方案10、方案4和方案11、方案5和方案12、方案6和方案13评价结果相近。 (2)MAGA-PPC模型的评价结果与模糊优选模型都确定方案9的水资源配置情况最优、方案12的水资源配置情况最差,在等级划分上MAGA-PPC模型与模糊优选模型存在一定的差异,即MAGA-PPC中凡采取了强化节水措施的方案均比不节水方案优,而模糊优选模型结果表明调水越多,方案越优;此外,MAGA-PPC模型评价后的投影特征值间的差异较为明显。 (1)相比现有的水资源配置评价方法,PPC在无需权重参与的情况下联通各参评指标间的数据信息,能够较为系统、精确地量化各方案在社会、经济、生态和资源等方面上的综合差异,且其评价结果与研究区的水资源开发利用状况和经济发展状况相符合,在水资源配置方案评价方面有很好的适应性。 (2)考虑到已有文献中对PPC建模合理性检验较少,以陕西省2020年水资源配置方案为例,从3个方面增设虚拟指标,并通过MAGA-PPC计算出的投影向量系数分析虚拟指标和评价指标的相关性,结果数值相同的指标的投影向量系数相等、所有样本数据完全相等的指标投影向量系数等于0、改变指标归一化方式后的指标投影向量系数为原指标的相反数,这表明MAGA-PPC模型编程和参数设置有效,该方法能够保证模型建立的合理性。 (3)陕西省内引汉济渭受水区2020年的水资源配置评价结果表明,MAGA-PPC模型能够客观、真实对水资源的配置情况做出评价。相比已有的水资源配置评价方法,PPC主要在大样本的情况下使用,对评价样本和指标的数量存在一定的要求,仍具有一定的局限性。3 算例分析
3.1 基础数据的收集
3.2 模型建立及验证
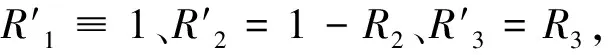
3.3 水资源配置方案评价
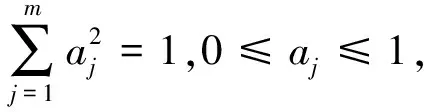
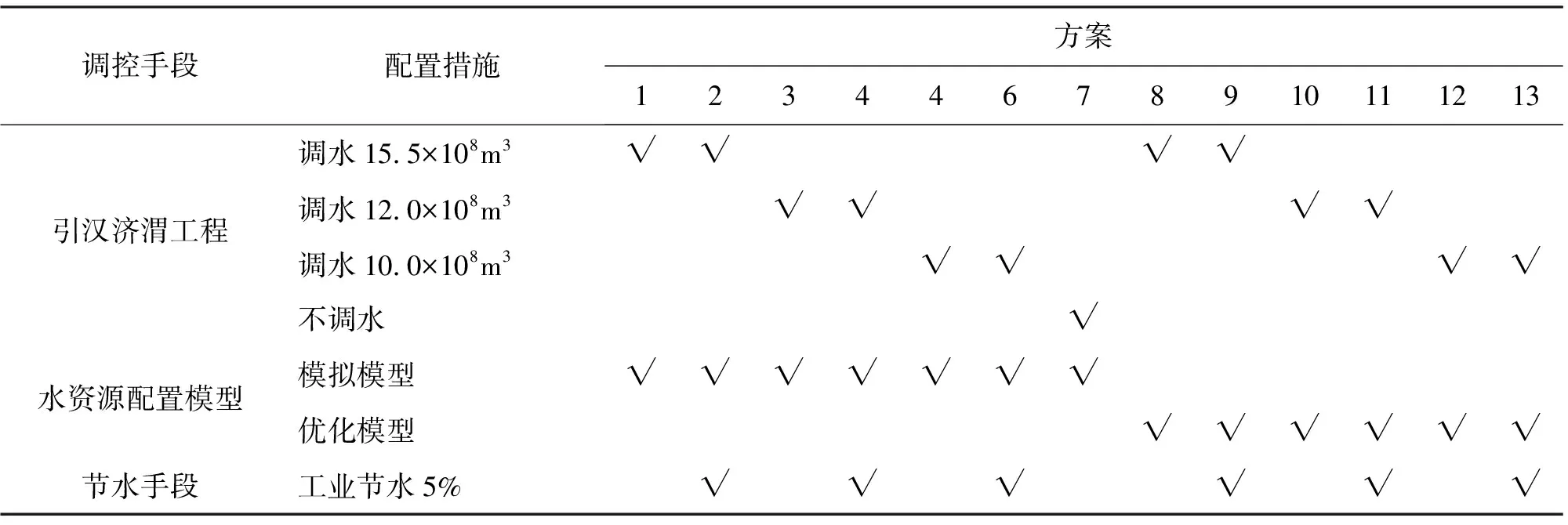
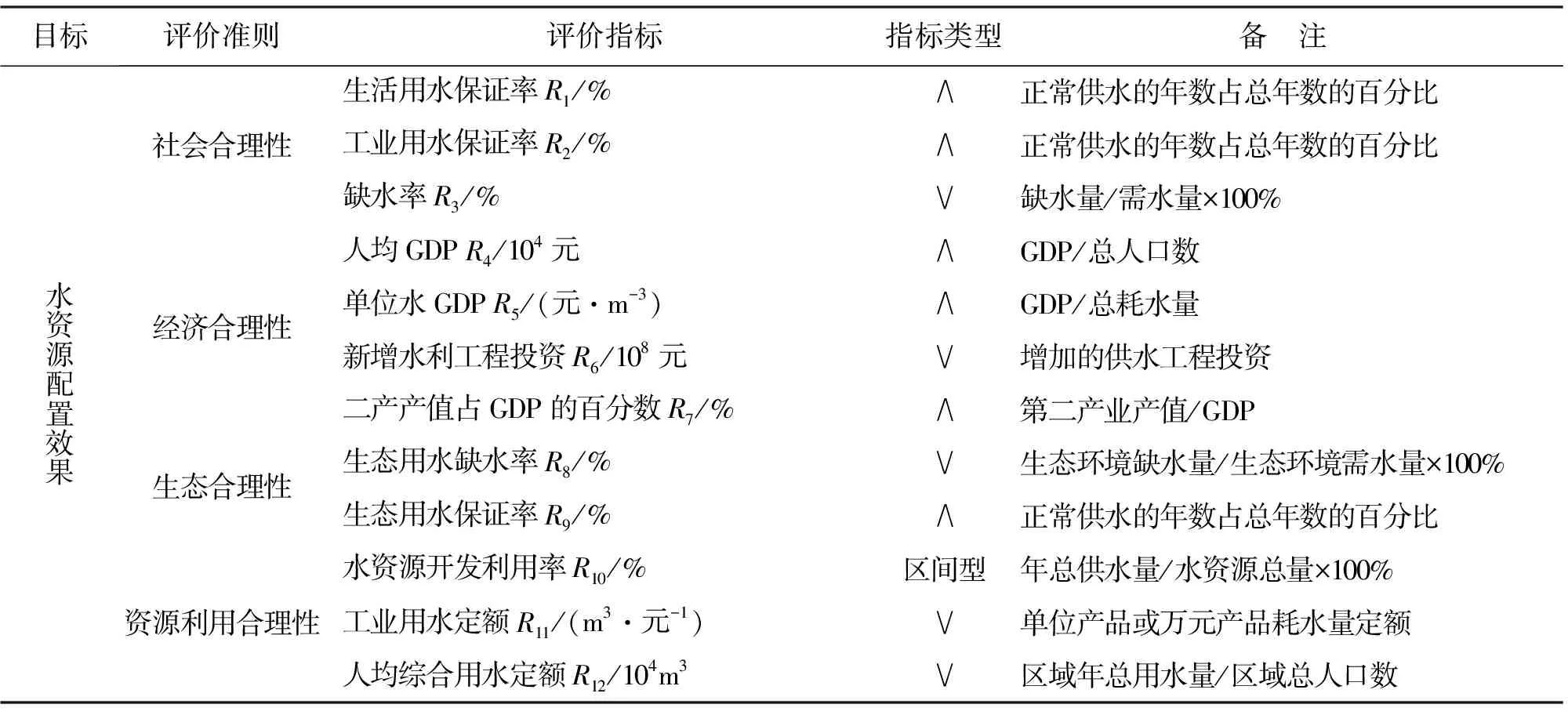

4 结 论
