“小导师制”下学生自主学习数学模式的构建
2018-07-21福建
福建
黄清波
(作者单位:福建省南安市国光第二中学)
“小导师制”下学生自主学习数学模式的构建
福建
黄清波
我校高三理科学生学习刻苦,态度端正,自觉性强,但相当多的学生对基础知识掌握较差,学习数学的气氛不太浓,差生面特别广,很多学生从基础知识到学习能力都有待提高,学生的数学学习普遍存在困难,2018年1月泉州市数学理科单科质检平均成绩在南安市排第21名,辅差任务非常重,形势非常严峻.如何提高学生数学学习积极性和学习效率?上学期期末我们让理科学生挤一小部分课余时间,试行“小导师制”下学生自主学习数学模式,一段时间以后,已经能有效地调动大部分学生的学习兴趣,激活学生的学习愿望.3月份泉州市质检理科数学平均成绩排名已上升到第18名,4月份省质检上升到第15名.本文将结合案例,阐述“小导师制”下学生自主学习数学模式构建的理解和思考.
一、“小导师”选聘
“小导师制”是指以合作小组为基本单位,从组内选拔“小导师”,“小导师”是数学成绩较好,乐于助人,且有一定的合作创新意识、口头表达能力、组织能力的学生.分组过程中,应确保各组间无明显差异,力求均衡,便于进行个人及小组的阶段性评价.老师应积极参与对各小组进行指导、跟踪、反馈、评价.各小组同学在每一位“小导师”的带领下,完成自学和小组学习、交流、讨论的内容,并保证组内每一位同学理解并掌握所学的数学知识.如我们班36人,可以分6组,根据实际情况,选聘6名“小导师”,按成绩每名“小导师”分配5位同学,落实“导师”职责.
二、“小导师”职责
1.制定活动计划,按时指导本组成员开展活动,明确任务分工,做到每次活动有主题、有主讲人、有效果,内容科学、合理.
2.活动前应充分准备,活动中努力调动成员的积极性,提高成员的参与度,培养成员的学习意识、合作意识.
3.每周做好活动的书面总结,向老师反馈本组的学习状态,存在问题或困惑,各组相互借鉴,取长补短,不断完善活动内容.
4.领导本组与其他组竞争,掀起比、学、赶、帮、超的学习气氛.
三、活动准备
1.时间安排:周日至周五18:20—18:40,每次活动20分钟左右,注重效率.
2.活动内容:活动不拘泥于形式,只要学生有收获、有启发、有触动,就能体现活动的价值.
(1)说题:题目可以是一个概念的解析、一个小专题归纳、一种题型的易错辨析或解题方法与技巧等,内容应是教学复习中的重点、难点、易错点、比较点、综合点、归纳点、演绎点和拓展点等关键点.题目可以说背景来源、命题立意、试题解法、拓展引申等.研究可深可浅,最好要有新观点,有一定新意,可操作,可学习,揭示一定的解题规律或命题规律.
(2)磨题:初始阶段可先由教师“出题”,让学生“磨题”,小组成员侧重分析题目的命题意图、试题简析、错解原因、题目来源,然后进一步变式、改编试题,达到解决与原问题相关的一类新问题的目的,使试题效益达到最大化.等到时机成熟后,可以让“小导师”出题,组员“磨题”.让学生有意识地进行解题锤炼、琢磨,努力掌握解题技能和了解解题的教学策略.
(3)质量分析:高三阶段有比较多的平时小测、周考、月考、各种质检等,每次规范性考试都有必要进行质量分析,对教与学起着反馈与调控的作用.首先,分析试卷的内容,考查哪些知识、能力、思想方法,考查哪些重点、难点、易错点等.其次,分析答题情况,本组平均分、最高分、最低分、各试题的得分情况,失分情况,什么原因造成失分,与其他组的差距.第三,今后措施,如何查缺补漏,如何发挥本组优势,如何借鉴其他组的成功经验.
3.活动形式:组员先独自思考,确定话题,整理要点、梳理活动思路,再组内共享,在讨论的基础上,达成共识,形成一周内的活动计划,成员轮流主讲,“小导师”负责协调,保证组内每一位同学理解并掌握所学的数学知识.
四、活动范例
【范例1】说题
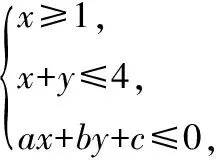
( )
A.2 B. 1
C. -1 D.-2
【说背景】本题是一道约束条件中含有参数的线性规划问题,是一个常考点,也是一个教学难点.学生解决这类问题会感觉困难,主要是因为这类问题含有参数使得要解决的问题处于动态变化之中,学生要么不知如何动笔,要么针对参数进行分类讨论时对变化因素考虑不周全,如何突破这一难点?
【说解法】分析:逆向思维,从目标函数入手,目标函数z=2x+y的最大值为7,最小值为1,对应直线2x+y=7和2x+y=1,结合已知条件对应的直线x=1和x+y=4,通过作图与求解即可确定使得目标函数z=2x+y取得最大值与最小值的点M和N,然后将这两点的坐标代入直线ax+by+c=0中,即可确定a,b,c之间的关系,进而使得问题得以顺利求解.


【说归纳】本题的求解思路就是从目标函数入手,打破了从正面入手根据图形确定目标函数取得最值的点来确定函数最值的常规求解,逆向思考问题,得到化繁为简、化难为易的解题效果.
【范例2】磨题(变题)

【命题意图】本题主要考查三角恒等变换;考查推理论证能力、运算求解能力等;考查化归与转化思想等;考查逻辑推理、数学运算等.难度一般,但答案易漏解.2018年全国卷Ⅰ第17题若考查数列,三角求值考查的可能性就很大.

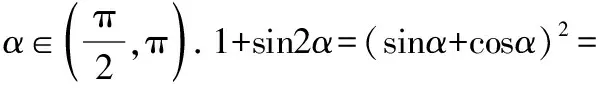

( )
【范例3】2018年省质量分析(试卷略)
试卷特点分析:覆盖知识面广,重点考查主干知识;注重思想方法,突显能力素养;贴近教材,增强思维难度;重视数学文化,呈现创新元素.
试卷答题情况:本组平均分、最高分、最低分、各试题的得分情况,失分情况,什么原因造成失分,与其他组的差距(具体分析略).
今后措施:进一步夯实基础,查缺补漏;回归教材,重视通性通法;抓住考点,精准备考,高效复习.

(作者单位:福建省南安市国光第二中学)
