引导学生关注数学运算能力的自育——例谈培养学生数学运算素养的实践

安徽

颜 军

浙江

余继光

(作者单位：安徽省滁州市明光市第二中学 浙江省绍兴市柯桥中学)

引导学生关注数学运算能力的自育
——例谈培养学生数学运算素养的实践

安徽

颜 军

浙江

余继光

一、数学运算能力的现象与关注

1.最近根据某校高三多项统考数学解答题答题卡(几千份)仔细逐题逐个思维链的研究统计数据显示，80%以上的解题失误是由于运算出错(数字计算、代数式计算、方程求解、不等式求解、运算性质的运用、计算方法的繁杂等).

2.为什么会出现大面积如此严重的数学运算能力下降现象？一是低年级阶段计算器的普遍使用，数字运算中的结构意识未训练，小学数字运算还没有毕业就升学到初中；二是初中阶段，在减负指标促使下，减少了代数式变形的训练，代数式运算的结构意识也非常弱，初中数学代数式运算还没有毕业就升学到高中；初高中虽有一周时间的衔接，但无法在短时间内弥补指数运算和对数运算需要螺旋上升才能进入学生的脑海中的现状.为此特呼吁教材专家在课程大纲制定中进行调整，使小学、初中、高中直到大学，整体上设计好数学知识层次要求，倾听一线数学教师的实践要求.

3.数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题.主要包括：理解运算对象、掌握运算法则、探究运算方向、选择运算方法、设计运算程序、求得运算结果.运算是构成数学抽象结构的基本要素，是演绎推理的重要形式，是得到数学结果的重要手段.数学运算是计算机解决问题的基础.通过数学运算核心素养的培养，学生能够提高解决数学问题和实际问题的能力，提升逻辑推理能力，形成程序化思考问题的习惯，养成实事求是、一丝不苟的科学精神.

二、数学运算能力的引导与策略

为了弥补上述已经出现在数学运算中的严重问题，一线教师在课堂教学中采取了一系列的补救措施，使教学目标能够艰难地落实.

1.引导学生关注自己的运算能力

不同层次的学生运算能力不同，统计调查表明，特别优秀的学生(如春季生、实验班、竞赛班等)在运算能力方面明显优于普通学生，因此，对于普通学生引导其关注自身的运算能力，如运算过程在草稿上落笔，以便发现自己是在“运算法则、运算方向、运算方法、运算程序”中的哪一个环节上问题更多，以便采取对策，及时纠正或调整.

2.在关键处强化学生的运算能力

在方程、不等式求解中，既强化规则，又提倡灵活；在函数性质教学中，加大代数式变形能力的训练量；在指数与对数运算教学中，加大教学力度与训练量；在三角函数教学中，加大三角恒等变换与变形的训练量；在平面向量教学中，注意形的运算不能代替数的运算；在空间图形教学中，三大角的坐标数字运算要快准；在圆锥曲线的方程与性质教学中，强化代数式运算.

3.估算、简算、计算顺序不能变

识字是语文的基础，运算是数学的基础，没有了基础，问题层出不穷.识字的关键是拼音，运算的关键是顺序，比如加减乘除与括号的混合运算，就要按照运算规则的顺序执行，数学运算中能心算就不要笔算，能估算就不要计算，能简算就不要繁算，如要计算不错尽量落地(草稿)生根，持之以恒，运算的正确率才能提升！

三、数学运算能力的自育与体验

数学运算能力的自我培养就是在教师的引导下，学生学会自己监控数学运算中可能出现的障碍，如数字加减乘除时不守规则；代数式变形运算时不化简而繁算；解方程与不等式时不化简且不检验；指数与对数运算时不遵守运算规则；三角函数求值或三角恒等变换时不注意运算方向；所有运算不在草稿纸上落笔等，并及时纠正，学会比较一个问题的两种算法(繁算与简算)；养成先化简后计算的习惯；面对复杂结构运算时先识别再计算；多种运算途径时，先明确方向再计算；当算式繁杂时，整体把握简化运算.

1.繁算与简算比较

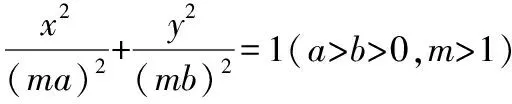
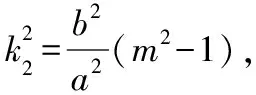
解法二：设C(x1,y1)，D(x2,y2)，

【解读】解法一，从代数角度理解题意，借助于方程思想求解，过程繁杂，但彰显通法运算能力；解法二，抓住切线方程的特点，借助于代数与几何关系，减少了部分运算，更显示综合分析能力，直线与圆锥曲线的综合问题离不开复杂的运算过程，只有驾驭了这一能力，才能遇“事”(运算障碍)不慌！

2.先化简后再计算

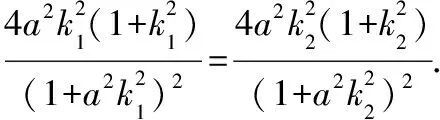
【解读】这是2016年浙江高考数学圆锥曲线题中的一个片段，专家多次强调要在圆锥曲线问题中检测考生的运算能力，其中解方程与解不等式是主旋律，上述的每一步都是学生在初高中数学学习中必须掌握的内容，但在综合运算时，由于运算方向不明确，变形能力弱而导致止步不前，失分严重.

【学习对策】不论是方程求解还是代数式变形，复杂的代数式运算中，第一有公因式要首先提出来或约去；第二遇无理式化有理式、分式化整式、多元化一元都是必须坚持的优先原则；第三不断地观察所面对的复杂代数式中的特点，以便采取下一步的运算方向.

3.先识别后再计算

代数式的结构识别，比如方程组中是否有特殊结构，它隐藏着什么？

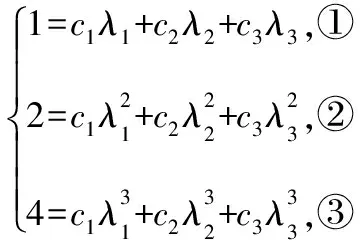
解法一：代入消元思想(求解过程相当复杂).

解法二：加减消元思想.

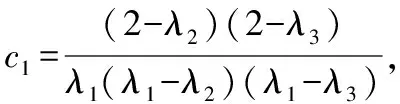
【解读】这是一个在探求长腿上楼梯的方法数时遇到的一个方程组，此方程组最大特点是字母具有对称性或称轮换式，不仅如此，每个方程之间联系紧密，结构特点明显，开始求解时，若运用代入消元思想，不仅过程相当复杂，而且难到无法表达问题解的程度，此例充分说明方法对于求解方程组或不等式的重要性.

4.明确方向再运算

( )

分析：根据题意，设PF1=r1，PF2=r2，可列方程组

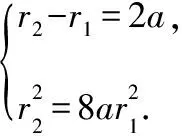
现象二：配方出错为4c2=(r1-r2)2-3r1r2.

【解读】初中学到的解方程及代数式变形方法，到高中后，由于方程或代数式的复杂程度提升，在变形过程中每一个细小的失误都可能导致大的解题失败，上述三个现象都说明了这一点.

【对策】把握运算方向；正确使用运算规则；时时观察代数式的结构特点，不论所面对的数学运算式子有多复杂，都要坚持这三条.

5.整体把握并检验

(Ⅱ)若sinC+sin(B-A)=3sin2A，求△ABC的面积.

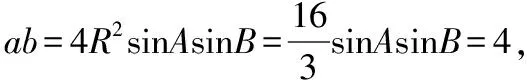
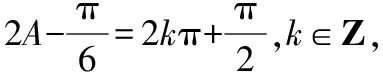
则a=2RsinA=2，b=2.

这种方法运算量大，运算过程复杂，若挖掘条件时整体把握运算方向，可简化过程.

解得a=b=2.

(Ⅱ)因为sinC=sin(B+A)，所以sinC+sin(B-A)=sin(B+A)+sin(B-A)=sinBcosA+cosBsinA+sinBcosA-cosBsinA=2sinBcosA，

所以2sinBcosA=3sin2A=6sinAcosA(*)

因此cosA=0或sinB=3sinA，

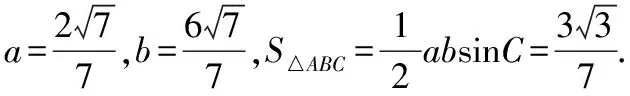
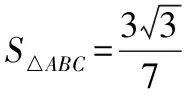
【解读】高三统考此题，解方程(*)中有78.6%的学生漏掉cosA=0，一方面可能有许多学生错误地判断cosA≠0，另一方面可能许多学生已经养成约分习惯，因此，整体把握试题并进行检验很重要.

四、总结

(作者单位：安徽省滁州市明光市第二中学 浙江省绍兴市柯桥中学)