基于数学核心素养的高考备考
——谈全国卷解析几何解答题
2018-07-21湖南
湖南
陈 健
(作者单位:湖南省株洲市第十三中学)
基于数学核心素养的高考备考
——谈全国卷解析几何解答题
湖南
陈 健
2014年3月30日,教育部印发了《教育部关于全面深化课程改革 落实立德树人根本任务的意见》,其中“核心素养体系”引人关注,研究提出各学段学生发展核心素养体系,明确学生应具备适应终身发展和社会发展需要的必备品格和关键能力,突出强调个人修养、社会关爱、家国情怀,更加注重自主发展、合作参与、创新实践.核心素养体系是深化课程改革、落实立德树人目标的基础,也是下一步深化工作的“关键”因素.
从双基教学的产生,到情感态度价值观、学生学科核心素养等一系列理念的提出、研究和实施,教育教学目标的实施逐步具体、明确、可操作.数学核心素养是相对于其他素养而言的,是专指一个人在事情处理过程中体现出来的数学方面的素质与水平的高低,或者是情境中某些因素激发了个人的数学认知结构,从而使得个人更多地从数学角度来看待问题.素养离不开具体的情境,数学素养只有在解决问题中才能体现出来.近几年全国高考数学试题充分体现了数学的六大核心素养(包含数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析),对深化课程改革、教材更新、引领数学教学等起到了积极的导向作用.
解析几何是高中数学的重要内容,其思想和方法贯穿了中学数学的全过程,可以有效地承载数学核心素养,所以每年高考全国卷无一例外至少有两小一大三个解析几何问题,22分以上.通过对解析几何解答题的深入研究,分析其典型试题的试题命制、解答过程、探究推广,能更具象化地揭示其所蕴含或要求的核心素养,也有利于强化培养学生数学核心素养的理念.
一、试题命制蕴含核心素养
(Ⅰ)求C的方程;
(Ⅱ)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1,证明:l过定点.
该题让学生利用椭圆的方程研究椭圆的几何性质.椭圆关于坐标轴对称,进而由条件确定四个点中的哪三个点在椭圆上,这是解析几何的核心、灵魂.第二问是直线过定点问题,是典型的用代数方法研究几何问题,最终回归几何问题.既考查学生的数形结合、分类讨论、等价转化等数学思想,又考查学生分析问题和解决问题的能力.通过试题的解答过程,可进一步体会蕴含的数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析等数学核心素养.
二、试题解析体现核心素养
【解析】(Ⅰ)由于P3,P4两点关于y轴对称,故由题设知C经过P3,P4两点.

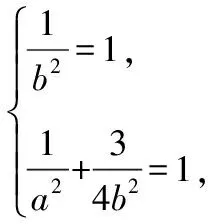
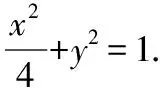
(Ⅱ)解法1:设直线P2A与直线P2B的斜率分别为k1,k2.

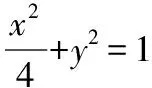
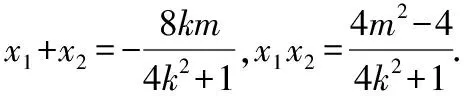

由题设知k1+k2=-1,故(2k+1)x1x2+(m-1)(x1+x2)=0.
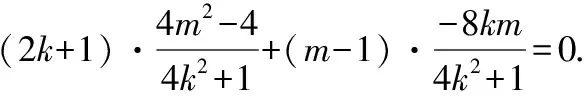

解法2:由题意可得直线P2A与直线P2B的斜率一定存在,不妨设直线P2A的方程为y=kx+1,直线P2B的方程为y=(-1-k)x+1.
将直线P2A的方程与椭圆C的方程联立得(4k2+1)x2+8kx=0,将直线P2B的方程与椭圆C的方程联立得(4k2+8k+5)x2-(8k+8)x=0.
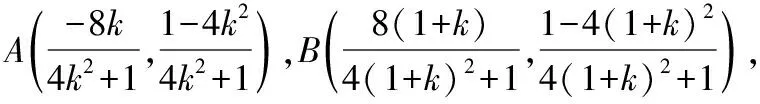


解法3:在坐标系中将原点O(0,0)平移到P(0,1),

由于直线l不经过O′(0,0),可设直线l在坐标系x′O′y′中的方程为mx′+ny′=1.
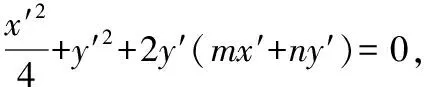

而直线l在坐标系x′O′y′中的方程为mx′+ny′=2m-2n,因此直线l在坐标系x′O′y′中过定点(2,-2),该点在原坐标系中的坐标为(2,-1),故直线l过定点(2,-1).
【评析】解法1是解析几何的常规方法,利用相关条件,联立椭圆与直线方程得到直线l方程中k与m的关系,求出定点,运算量较大.解法2通过直接设直线P2A的斜率,避免了对直线l的斜率是否存在的讨论,也减少了参数的个数,简化了运算.解法3将两直线的交点平移到坐标原点使直线斜率和的代数形式变得简单,再联立方程利用根与系数的关系找到m与n的等量关系,得出定点.三种解答都充分体现了数学核心素养对解题思路的引领,解法都通过数学抽象,分别建立了对应的数学模型,再逐步进行逻辑推理和数据分析、数学运算来简化问题,最后使问题得以解决.
(4)纸浆洗涤过程t时刻的工艺指标为o(t)=[o1(t), o2(t), o3(t)]。其中,o1(t)为纸浆洗涤质量,o2(t)为出浆产量,o3(t)为耗损费用。
三、试题探究培育核心素养
本题具有很好的教育价值,不应仅仅停留在问题的解答上,可以进一步挖掘其深层次的数学内涵,揭示数学本质.引导学生进行如下探究:
1.若将斜率之和为-1换为任意实数m,是否也有类似结论

2.将点P(0,1)换成椭圆其他顶点是否有类似结论

3.若将椭圆方程一般化,可否得到类似的结论

4.若点P换为椭圆上任一点,是否有更一般的结论
5.类比双曲线,是否也有类似的结论
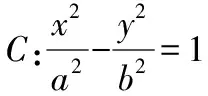
6.对于抛物线,是否也有类似的结论

探究的过程由浅入深,从具体数到字母,从特殊到一般,从椭圆到双曲线和抛物线,通过变式教学、类比推广,引导学生对试题进行研究探索,不断揭示数学本质,形成一般结论,在此过程中数学抽象能力得到不同程度的发展与提升.通过逐步积累、领悟、内省,培养学生学会用数学眼光观察世界,用数学思维分析世界,用数学语言表达世界,从而有效地促进学生数学核心素养的培养与提高.
四、对高考复习备考的启示
1.积极主动地推进数学核心素养的落实
数学核心素养不是应试教育所培养的“低级素养”,如死记硬背的素养、题海战术的素养等.为此,在教法上要变直接讲授为分析问题的依存关系,再选择合适解法,突出讲练的实效性,克服完全依赖教辅资料的习惯,使课堂充满思辨、充满生机.
2.建立学科思想,提高课堂效率
高三数学复习内容多、时间短、任务重,但解决问题的方法绝不单纯是“串讲”加“练习”,而应该是学科思想与重点训练相结合,让学生在理性思维的引领下,有意识、有目的地高效练习,让我们的学生满腔热情地投身到火热的高三备考中来.
3.研究考纲和试题,提高复习的针对性

(作者单位:湖南省株洲市第十三中学)
