一道线性规划问题的“华丽变身”

内蒙古

姬恩泽

(作者单位：内蒙古通辽市通辽实验中学)

一道线性规划问题的“华丽变身”

内蒙古

姬恩泽

线性规划问题是近几年高考的热点,也是变化模式最丰富的一种命题形式.线性规划虽然作为直线方程的一个简单应用,但是它的考查趋向于灵活多样,并且通常与其他知识进行交叉融合, 体现了高中数学常用的数学思想,如数形结合思想,转化与化归思想,也体现新课标“学数学,用数学”的理念,考查学生综合分析问题的能力,逻辑思维能力以及解决实际问题的能力,因此很受高考出题者青睐.下面对一道线性规划问题从知识要求、能力要求、学科思想、试题难度等角度进行多维度分析,并进行多方位的变式.

( )

A.[1,5] B.[2,6] C.[2,10] D.[3,11]

1.了解线性规划模型的特征：一组决策变量(x,y)表示一个方案；约束条件是一次不等式组,熟悉线性约束条件(不等式组)的几何表征是平面区域(可行域),并能准确画出可行域；

【试题能力要求以及蕴含学科思想】经历观察、分析、操作、归纳、概括等认知过程,还必须要具备联想、作图和解决实际问题的能力.教师应培养学生数据分析能力、探究能力、合情推理能力以及运用已有知识解决新问题的能力,突出体现优化思想、数形结合思想和化归思想.

【试题难度】本类题目需要画出可行域的图形,并会用数形结合思想求出目标函数的最值,难度中等.

【试题易错点】由于目标函数是求两点连线的斜率,特别需要注意的是斜率不存在(即倾斜角为90°)的情况,还要重视求斜率的倒数形式的题型.

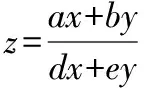
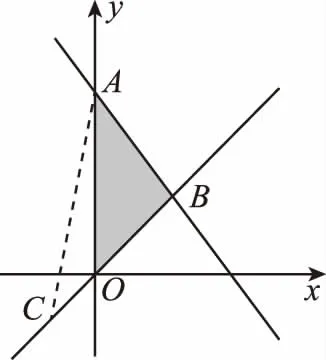
从变式1和变式2看出,目标函数变形的过程难度加大了,但是目标函数的分子和分母仍然都是关于x,y的线性表达式,并且都能化归为斜率型目标函数的形式,那么如果去掉目标函数的分母,并且引入绝对值表达式,就使得目标函数的几何意义更加“扑朔迷离”,从而提高了试题的难度,由此得到变式3.

可以看到变式3的目标函数引入绝对值表达式后,目标函数的几何意义已经从斜率型成功转化成了点到直线距离的类型,让人有耳目一新的感觉,使得这类斜率型目标函数“独揽大权”的局面得以扭转.那么目标函数还可以怎么转化,才能让这类规划问题更加丰富多彩呢？下面尝试把表达式中的变量x,y之间的线性运算改为乘法,就得到变式4.

可以看出,变式4的目标函数实现了从“一次”到“二次”的转化,那么为了使目标函数更加“隐形”,可以再次把二次函数与分式表达式结合起来,使目标函数从外观上看着更加“高大上”,由此得到变式5.

经过逐步“改装”后的变式6,确实是“与众不同,气质非凡”了,但是再仔细揣摩变式6,发现它的约束条件太过于“平常”,可以重新“包装”它的约束条件,才能使该题趋于完美,由此得到变式7.

(作者单位：内蒙古通辽市通辽实验中学)