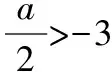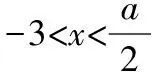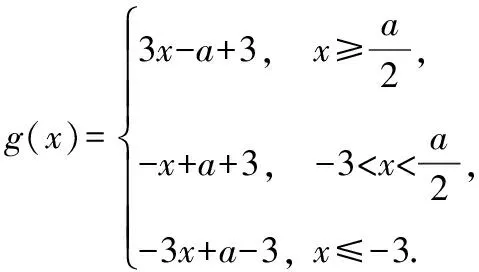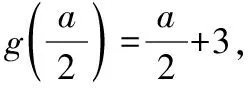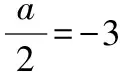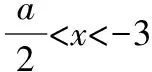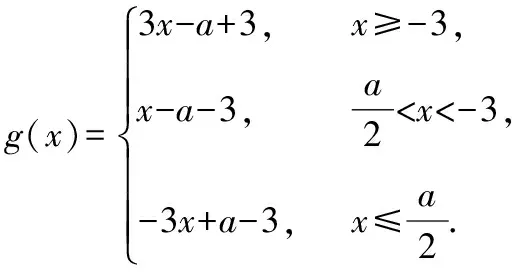对一道“不等式选讲”试题的多角度研究

广东

郑荣坤

(作者单位：广东省揭阳市惠来县第一中学)

[编者按]变式教学、变式思想是数学教学及学习过程中比较重要的一种途径和方法.本文从试题解法研究到变式研究，解法与变式相呼应，整体逻辑完整，变式角度清晰，以期为读者变式方面的探索及进一步研究有所启发.若您希望与更多老师一起探讨研究，欢迎加入数学变式研发兴趣QQ群：745207957.

对一道“不等式选讲”试题的多角度研究

广东

郑荣坤

选考题分值为10分，是学生必争的高分值考题.之前学生还可以从“几何证明选讲”、“坐标系与参数方程”和“不等式选讲”中任选一题作答，但是从2017年开始就删除了“几何证明选讲”，现在“坐标系与参数方程”与“不等式选讲”就更为重要了.由于大多数学生的解析几何基础比较薄弱，所以会选做“不等式选讲”，可是许多学生不能得满分.摆在高三数学教师面前的这个难题，要怎么突破呢？笔者通过对一道“不等式选讲”试题的多角度研究，帮助高三师生梳理“不等式选讲”的常见考题及其解题方法，与高三数学教师共同探求解决上述难题的突破口.

一、呈现试题

试题：已知函数f(x)=|x-a|.

(1)若a=1，解不等式f(x)≥4-|x-1|；

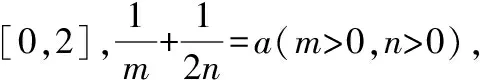
【评注】上述试题是2017年安徽省马鞍山市第一次模拟考卷第23题，试题的第一小问主要考查绝对值不等式的解法，第二小问考查条件最值.

二、对试题解法的研究

1.研究试题第一小问的解题方法

试题第一小问考查学生对绝对值不等式解法的掌握情况.因为若a=1，f(x)=|x-1|，所以不等式f(x)≥4-|x-1|可化为|x-1|≥2，求解此类绝对值不等式，一般有下列四种方法.

方法1(分类讨论去绝对值)：

①当x≥1时,x-1≥2，解得x≥3；

②当x<1时，1-x≥2，解得x≤-1.

综上所述，不等式的解集为{x|x≥3或x≤-1}.

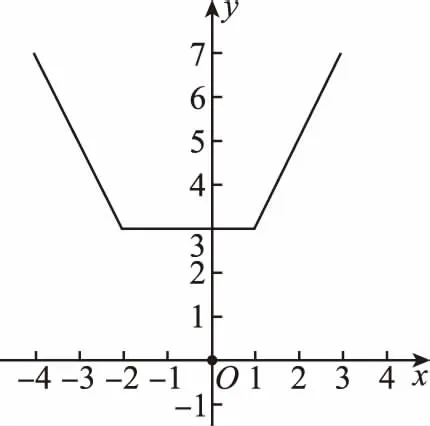
方法2(图象法)：设g(x)=|x-1|，则y=g(x)的图象如图所示，由图象可知，不等式的解集为{x|x≥3或x≤-1}.

方法3(平方法)：两边平方得，(x-1)2≥4，整理得x2-2x-3≥0，解得x≥3或x≤-1.因此，不等式的解集为{x|x≥3或x≤-1}.

方法4(绝对值几何意义)：由于|x-1|≥2，则x-1≥2或x-1≤-2，解得x≥3或x≤-1.因此，不等式的解集为{x|x≥3或x≤-1}.

【评注】求解绝对值不等式除了分类讨论去绝对值法、绝对值几何意义法、图象法外，有时也可以用平方法，但平方法要注意不等式两边式子的符号，例如|x-1|≥-2，不等式左边大于或等于零，右边小于零，不能直接平方求解.上述四种方法中分类讨论去绝对值法、绝对值几何意义法最具有普遍性，而绝对值几何意义法求解过程最简洁.

2.研究试题第二小问的解题方法

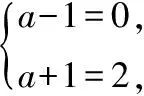
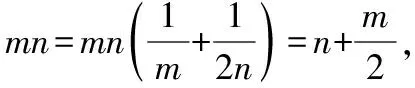
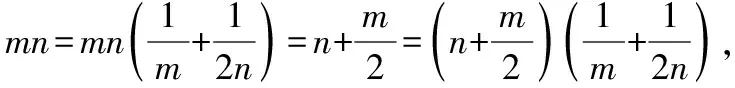
【评注】求解“条件最值”可以活用约束条件中的“1”，也可以利用基本不等式或柯西不等式变形目标函数后分离变量，如果从几何和三角视角去看“条件最值”，那么也可以采用构造函数法、三角换元法.

三、对试题变式的研究

1.从解不等式的角度进行试题变式

变式1：已知函数f(x)=|x-a|，若a=1，解不等式f(x)≥4|x+1|-|x-1|.

解：若a=1，f(x)=|x-a|=|x-1|，不等式f(x)≥4|x+1|-|x-1|可化为|x-1|≥2|x+1|.

进行分类讨论，

①当x≥1时,x-1≥2x+2，解得x∈∅；

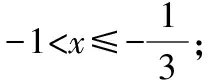
③当x≤-1时，1-x≥-2x-2，解得-3≤x≤-1.

本题也可用平方法或图象法求解.

变式2：已知函数f(x)=|x-a|，若a=1，g(x)=f(x-2)-f(x+2)，求不等式|g(x)|≤2的解集.

解：若a=1，f(x)=|x-1|，则g(x)=|x-3|-|x+1|.

①当x≥3时,|x-3|-|x+1|=x-3-x-1=-4，不满足题意，舍去；

②当-1

解得0≤x≤2；

③当x≤-1时，|x-3|-|x+1|=3-x+x+1=4，不满足题意，舍去.

综上所述，不等式的解集为[0,2].

本题还可用图象法求解.

【评注】“绝对值不等式的解法”是近几年来高考的热门考点，常作为“不等式选讲”第一小问，它是很多学生的主要得分点，最常见的解法有图象法、分类讨论法，当然，也可以根据题目的特点挖掘其他解法，例如变式1还可以转化为|x-1|≥2|x+1|后，两边平方去求解.

2.从最值的角度进行试题变式

变式3：已知函数f(x)=|x-a|，若a=1，关于实数x的不等式f(x)

解：若a=1，关于实数x的不等式f(x)

设g(x)=|x-1|+|x+2|,

①当x≥1时,g(x)=|x-1|+|x+2|=x-1+x+2=2x+1；

②当-2

③当x≤-2时，g(x)=|x-1|+|x+2|=1-x-x-2=-2x-1.

因此，实数m的取值范围为(-∞,3].

本题还可用绝对值三角不等式法和绝对值几何意义法，|x-1|+|x+2|的几何意义为实数x到实数1与到-2的距离之和.

【评注】“求绝对值函数的最值”是近几年来高考的高频考点，常出现在第二小题，常见的解法有:零点分段法、绝对值几何意义法、绝对值三角不等式法，而比较上述的三种解题方法，常常会发现绝对值三角不等式法的解答过程较为简洁.

3.从含参数的角度进行试题变式

变式4：已知函数f(x)=|x-a|，g(x)=log2[f(x)+|x+3|]，若g(x)的值域为[1,+∞)，求实数a的值.

解：由于函数f(x)=|x-a|，则g(x)=log2(|x-a|+|x+3|),若g(x)的值域为[1,+∞)，则log2(|x-a|+|x+3|)≥1，即|x-a|+|x+3|≥2.

由于|x-a|+|x+3|≥|(x-a)-(x+3)|=|a+3|，则|a+3|=2，解得a=-1或a=-5，因此，实数a的值为-1或-5.

本题使用的方法为绝对值三角不等式法，还可用零点分段法求解.

变式5：已知函数f(x)=|x-a|，g(x)=f(2x)+|x+3|，若g(x)的最小值为4，求实数a的值.

解:由于函数f(x)=|x-a|，则g(x)=|2x-a|+|x+3|.题目变为若|2x-a|+|x+3|≥4,求实数a的值.

③当x≤-3时，g(x)=|2x-a|+|x+3|=a-2x-x-3=-3x+a-3.

画出函数图象可知，函数g(x)的最小值为

①当x≥-3时，g(x)=|2x-a|+|x+3|=2x-a+x+3=3x-a+3；

本题使用方法为零点分段法，还可用绝对值三角不等式法.

变式6：已知函数f(x)=|x-a|，g(x)=f(x)+|x+3|，h(x)=f(x+a-5)+2，若∀x1∈R,∃x2∈R使得g(x1)=h(x2)，求实数a的取值范围.

解：由于h(x)=f(x+a-5)+2=|x-5|+2≥2，则函数h(x)的值域为[2,+∞)，由于g(x)=f(x)+|x+3|=|x-a|+|x+3|≥|(x-a)-(x+3)|=|a+3|，则函数g(x)的值域为[|a+3|,+∞)，由于∀x1∈R,∃x2∈R使得g(x1)=h(x2)，则[|a+3|,+∞)⊆[2,+∞)，则|a+3|≥2，解得a≥-1或a≤-5.因此，实数a的取值范围为(-∞,-5]∪[-1,+∞).

变式7：已知函数f(x)=|x-a|，g(x)=2f(x)-|x+3|，当a>-3时，若函数f(x)的图象与x轴所围成的封闭图形的面积不超过54，求实数a的取值范围.

解：由于函数f(x)=|x-a|，则g(x)=2f(x)-|x+3|=2|x-a|-|x+3|，a>-3.

①当x≥a时,g(x)=2|x-a|-|x+3|=2x-2a-x-3=x-2a-3；

②当-3

③当x≤-3时，g(x)=2|x-a|-|x+3|=2a-2x+x+3=-x+2a+3.

函数y=g(x)的图象如图所示，由图象可知，函数f(x)的图象与x轴所围成的封闭图形的面积为

【评注】上述变式是笔者根据高考真题、各地模拟卷考题改编而成，都是“不等式选讲”的常考试题.而含参数的绝对值函数求最值，既可以采用零点分段法，也可以采用绝对值三角不等式法.对于求解“任意性与存在性”函数最值，实际上就是确定值域与值域之间的关系，如果将上述变式6中的条件“∀x1∈R,∃x2∈R使得g(x1)=h(x2)”改为“∀x1∈R,∃x2∈R使得g(x1)≥f(x2)”，则为gmin(x)≥fmin(x).

(作者单位：广东省揭阳市惠来县第一中学)