做题与变题——教师自我提升的有力支撑

山东

尹承利

(作者单位：山东省泰安市泰安英雄山中学)

做题与变题
——教师自我提升的有力支撑

山东

尹承利

数学教师的成长和自我提升离不开题目，数学课堂教学需要题目，在题目的不断变化中可以寻找到问题的真谛.在课堂上，教师对题目的讲解如行云流水、得心应手，这凝聚了教师课下做题、变题的心血.教师通过做题和变题，可以体会问题的价值和意义，是自我提升教学境界的有力支撑.

一、做题

数学教师离不开做题，做题是数学教师的基本功.通过不断地做题，能提升数学教师的思维品质，并能帮助教师在课堂上更好地教学，真正达到“要给学生一杯水，教师应有一桶水”的境界.那么，做什么题，做多少题，怎样做题是有很大区别的.其实，教师应首先做透教材中的题目和高考真题.教材上的题目是编写者配合基本知识精心编拟的问题，是学生进一步学习的基础，许多题目也是后面解决问题的工具.不少教师对教材上的题目疏于研究，这是本末倒置的表现，是不可取的.高考真题具有很强的典型性和思维性，是命题者精心设计的问题，是对考试大纲的具体诠释，对教师很好地把握教学、复习具有很强的指导意义和导向性，所以高考真题是教师必须做好、做透的好题目.当然，教师做题应倡导不急于看解析和答案，要在无解析、答案的状态下思考分析，真正感受题目的本质、体会题目的难易程度，这样做题将使教师最贴近学生的实际，能真正体会到学生做题的感受，对教学会有很大的帮助.

【规律分析】平面向量既反映了数量关系，又体现了几何图形的位置关系，从而将数和形有机地结合起来.向量有关问题的求解通常有两种思路：一是“数化”，即利用平面向量的代数运算或坐标运算，把问题转化为代数中的方程、不等式等问题；二是“形化”，即利用平面向量的几何意义将问题转化为平面图形的特征直接进行求解.

方法1.代数运算方法

平面向量的代数运算是指向量的线性运算(加法、减法和数乘，运算的结果还是向量)和向量的数量积运算(运算的结果是一个数量)，向量的代数运算是最常见、最基础的运算，特别地，数量积运算是向量实数化的桥梁.

解法1:利用数量积运算

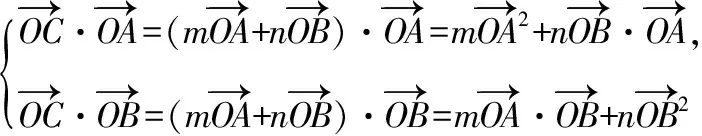
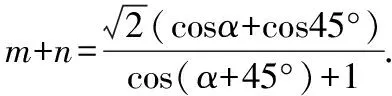
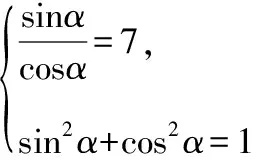
【点评】本解法从向量的模和夹角出发，巧妙地利用向量的数量积运算和三角恒等变换求解，很富有创意.

方法2.坐标运算方法

向量坐标法，即建立恰当的直角坐标系，将问题用坐标表示，通过向量的坐标运算，使问题简单化，程序化，坐标法的优点是目标明确，思维难度小.

解法2:利用向量的坐标运算

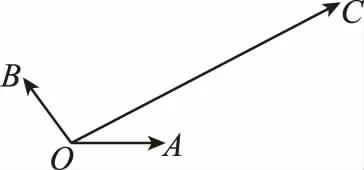
如图，以点O为坐标原点，以OA所在的直线为x轴建立平面直角坐标系，

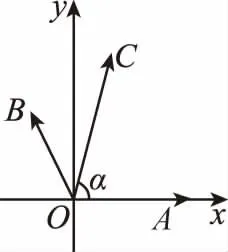
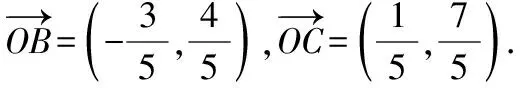
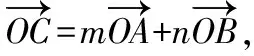
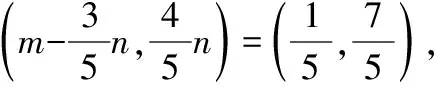
【点评】利用平面向量的坐标运算，我们可以把向量运算代数化.将数与形紧密结合起来，从而使许多问题转化为我们熟知的数量运算，使问题得以简化.本解法是通过建立平面直角坐标系，构设点的坐标后转化为向量的坐标运算，利用向量相等转化求解，体现了数学建模思想的运用.

方法3.几何方法

几何方法就是捕捉向量“形”的特征，挖掘图形中的几何性质，运用数形结合的思想方法解题.几何方法往往能使难题变得简单.

解法3:利用向量的运算法则

如图，过C作OB的平行线交OA的延长线于A′，作OA的平行线交OB的延长线于B′.

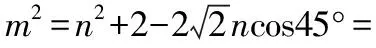
【点评】本解法利用向量加法的平行四边形法则，并结合三角形中的余弦定理，将问题几何化，体现了数形结合思想的运用.

方法4.利用向量三点共线定理和等积法

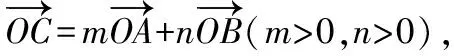
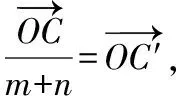
由S△AOC′+S△BOC′=S△AOB，得

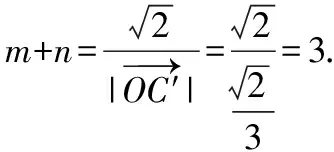
【点评】本解法巧妙地构造三点共线模型，并利用三角形的等面积法求解，思维独特、匠心独具，对拓展学生的解题思维颇有裨益.

模型提炼

这是一类高考中常出现的向量问题，相关的高考题还有：

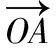
(Ⅰ)求直线AP斜率的取值范围；

(Ⅱ)求|PA|·|PQ|的最大值．

【规律分析】解析几何问题的本质是把几何问题转化为代数问题，通过代数运算研究几何图形性质，图形问题代数化是解析几何的本质.利用函数建模能为解答最值问题增添一抹亮色.解析几何的关键在于找到最好的方法解决问题.借助数形结合，大胆运用平面几何相应地性质，相比用固定解题程序，则能更快地找到简捷的解题方法.即解析几何问题要注重对问题本质的提炼，并与相关知识的联系(如平面几何、向量、函数、方程、不等式等)进行合理转化，就会有精彩的解答.

方法1.解析法视角

(Ⅱ)联立直线AP与BQ的方程

所以|PA||PQ|=-(k-1)(k+1)3.

【点评】本题主要考查直线方程、直线与抛物线的位置关系等基础知识，同时考查解析几何的基本思想方法和运算求解能力，通过表示|PA|与|PQ|的长度，构造函数f(k)=-(k-1)(k+1)3求解|PA|·|PQ|的最大值.

方法2.几何法视角

解法2：构建几何模型，利用二次曲线的相切求解

(Ⅰ)略；

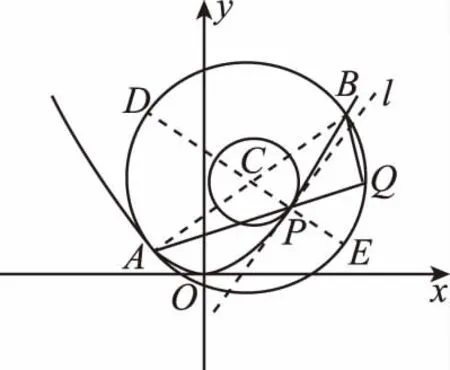
根据相交弦定理，得

根据图形，当以C为圆心的圆与抛物线相切于点P时，|CP|取得最小值.

设直线l与以C为圆心的圆与抛物线相切于点P(t,t2).由y=x2，得y′=2x，切线l的斜率为2t.

【点评】本解法运用了平面几何中圆的有关性质：直径所对的圆周角为直角、圆中的相交弦定理等知识，数形结合优化思维、简化计算；然后利用公切线解决二次曲线相切问题、因式分解等技巧.其中对于三次式的因式分解是需要认真领悟和掌握的.

解法3：构建几何模型，构造函数利用导数求解

同解法2，得|PA|·|PQ|=2-|CP|2.

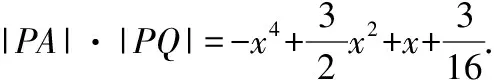
则f′(x)=-4x3+3x+1=-(x-1)(2x+1)2.

令f′(x)=0，得x=1.

【点评】本解法与解法2相近，在运用平面几何中圆的有关性质的基础上，通过构造函数，结合导数求得最值.

解法4：构建几何模型，配方利用非正数的性质求解

【点评】本解法没有像解法3那样，得到关于x的四次函数式后，运用导数知识求解最值.而是运用常见的配方法解决了高次函数的最值问题.角度新颖，思维深刻，几何背景搭台，代数方法唱戏，实有创新.

方法3.向量法视角

解法5：构建向量模型，构造函数利用导数求解或配方利用非正数的性质求解

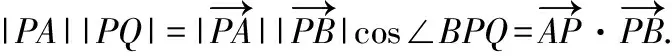
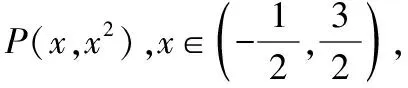
以下利用导数求最大值的过程同解法3或利用配方求最大值的过程同解法4.

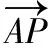
方法4.参数法视角

解法6：构建参数方程模型，构造函数利用导数求解或配方利用非正数的性质求解

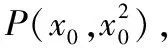
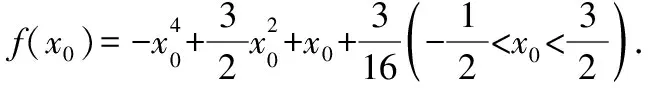
以下利用导数求最大值的过程同解法3或利用配方求最大值的过程同解法4.

【点评】此解法最为简单，线段长度之积，考试时联想到参数方程解答这道题会更简洁利索些.

二、变题

教师自我发展的途径可能有多条，其中对题目进行变式就是一条切实可行的途径，经常想着如何将题目横向、纵向拓展，以一当十、触类旁通，可以有效地提高教学效率.那么，教师如何对典型题目进行变式呢？变题主要靠的是联想，要浮想联翩，思绪万千，沿着蛛丝马迹，寻芳采猎，刨根问底.试探、猜想、组拼、嫁接、改编、重塑、加工、修补、完善.也要勤阅读，在阅读中思考，不时会有灵感，随时记录，便可形成一些新题目.

提倡要在做题的基础上变题，要想变式出上乘的好题，做题功夫至关重要.在做题中悟道，促发联想，揣摩原编题者的意图，设计变式措施，窥视各个题目的联系，找出题根，实现迁移.要注重对题目多解、多思，引申拓宽，提纲挈领，居高临下，横联纵串.记录采摘，挖本质、掘内涵、勤思考，为题目的变式积累丰富资源.

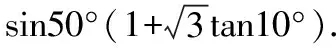
解法1：

解法2：

【点评】三角函数的化简、计算、证明等问题中三角恒等变换的基本思路是：一角二名三结构.即首先观察角与角之间的关系，注意角的一些常用变式，角的变换是三角函数变换的核心！二看函数名称之间的关系，通常“切化弦”；第三观察代数式的结构特点.本题的两种解法，变角、变名和变式等常用的变换技巧都得到了体现和应用.

若结合应用二倍角公式改变所化简的式子，可有如下变式：

【分析】先逆用二倍角的余弦公式，再应用诱导公式变角、变名后，即化为例题的形式.

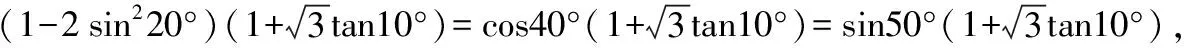
【点评】本变式在例题的基础上作了引申，逆用二倍角余弦公式和应用诱导公式化为例题求解的.

若改变化简式子的形式，可有如下变式：

【分析】首先切化弦，变角、变名后利用二倍角正弦公式通分，再变角应用两角和的正弦公式展开.也可以利用10°=60°-50°与两角和的正切公式展开，再进行切化弦，最后统一角和函数即可.

解法1：

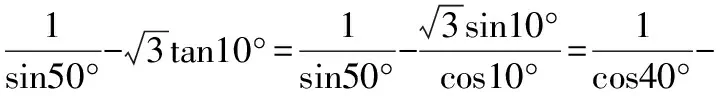
解法2：

【点评】与例题相比，本变式的变换更为多样——解法1首先切化弦，变角、变名并应用二倍角正弦公式通分，拆角40°=30°+10°，应用两角和的正弦公式展开即可；解法2“曲径通幽 ”，首先变角10°=60°-50°，后利用两角差的正切公式，再切化弦转化到解法1的过程，虽然“绕道”，但也值得玩味.

若将所化简的式子渗透参数，逆向求参，可有如下变式：

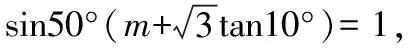
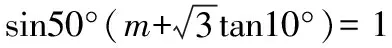
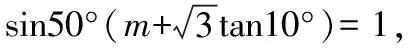
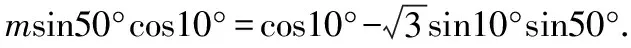
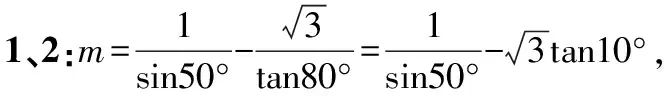
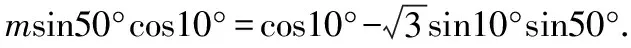
以下同变式3的解法3.

【点评】这两个变式以考查学生能力立意为起点，改变了三角恒等变换的考查层次，把问题放在学生既熟悉、又陌生的环境中；它源于课本，又高于课本，难度远远高于课本，在问题的处理过程中，很好地利用了处理三角函数问题的基本思想方法.本变式的处理方法灵活多样，是一道提升学生能力的好题.

若设计为探索性问题，可有如下变式：

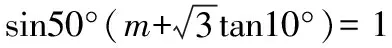
【分析】在假设存在的前提下，按变式3的方法进行变换求解.

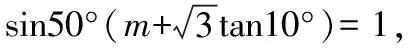
【点评】本变式设计为探索性问题，不落窠臼，使对三角恒等变换的知识、基础和思维能力的考查更为深入，是一道精彩的变式题.

(作者单位：山东省泰安市泰安英雄山中学)