高考数学文化题组训练
2018-07-20山东尹承利
山东 尹承利
一、以函数为背景的数学文化题

1.(2017·河南六市联考)中国传统文化中很多内容体现了数学的“对称美”.如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分体现了相互转化、对称统一的形式美、和谐美.给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:
①对于任意一个圆O,其“优美函数”有无数个;
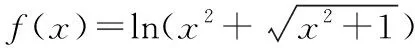
③正弦函数y=sinx可以同时是无数个圆的“优美函数”;
④函数y=f(x)是“优美函数”的充要条件为函数y=f(x)的图象是中心对称图形.其中正确的有
( )
A.①③ B.①③④ C.②③ D.①④
【解析】对于①,过圆心的任一直线都可以满足要求,所以正确;对于②,可以作出其图象如下,
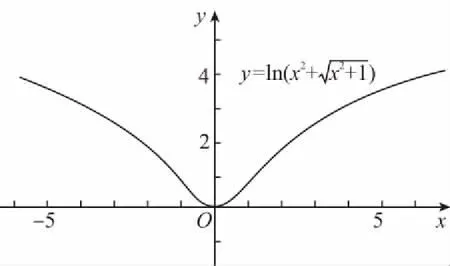
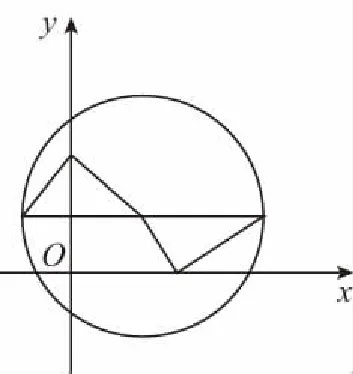
故不能是某圆的优美函数;对于③,只需将圆的圆心放在正弦函数的图象的对称中心上即可,所以正弦函数是无数个圆的优美函数;对于④,函数是中心对称图形时,函数是优美函数,但是优美函数不一定是中心对称,如图所示,故选A.
二、以三角为背景的数学文化题
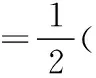
( )
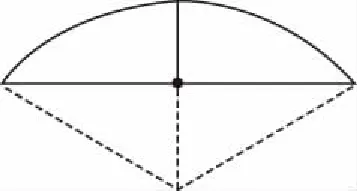
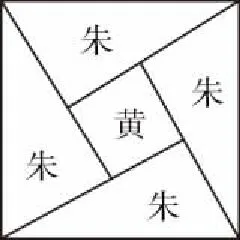
A.6平方米 B.9平方米
C.12平方米 D.15平方米
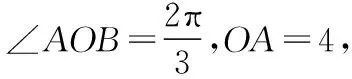
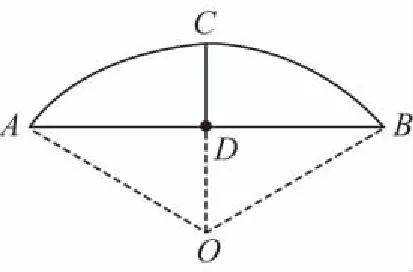
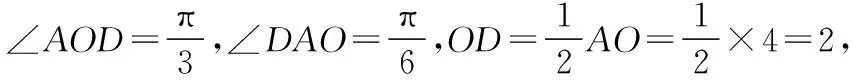
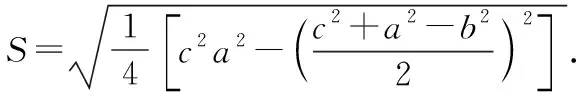
( )
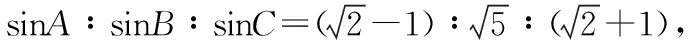
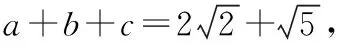

则ac=2-1=1,c2+a2-b2=6-5=1,
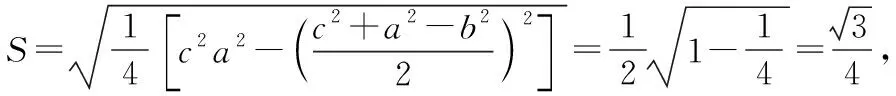
三、以数列为背景的数学文化题
1.(2017·安徽江南十校联考)《九章算术》是我国古代的数学名著,书中《均输章》有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知A,B,C,D,E五人分5钱,A,B两人所得与C,D,E三人所得相同,且A,B,C,D,E每人所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).在这个问题中,E所得为
( )
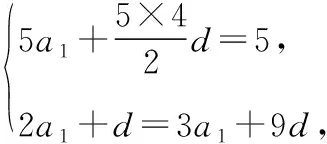
2.(2017·湖南衡阳八中月考)中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”则该人最后一天走的路程为
( )
A.24里 B.12里
C.6里 D.3里
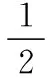
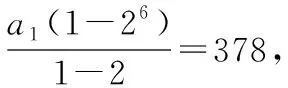
3.(2017·湖北黄冈期末)“中国剩余定理”又称“孙子定理”.1852年英国来华传教士伟烈亚利将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将2至2 017这2 016个数中能被3除余1且被5除余1的数按由小到大的顺序排成一列,构成数列{an},则此数列的项数为________.
【解析】能被3除余1且被5除余1的数,即为被15除余1的数,易知,被15除余1的数构成以16为首项,15为公差的等差数列.
由题意得16+15(n-1)≤2 017,解得n≤134.4.故此数列的项数为134.
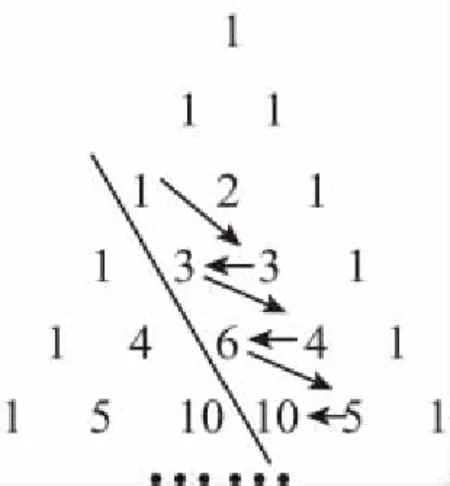
4.(2017·北京博恩教育模拟)如图,在“杨辉三角”图形中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10,6,15,…,则a2017的值为________.

四、以不等式为背景的数学文化题
1.(2017·湖北黄冈质检)关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计π的值:先请200名同学,每人随机写下一个都小于1的正实数对(x,y),再统计两数能与1构成钝角三角形三边的数对(x,y)的个数m;最后再根据统计数m来估计π的值,假如统计结果是m=56,那么可以估计π=________.(用分数表示)
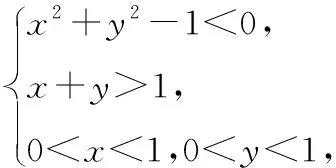
五、以立体几何为背景的数学文化题
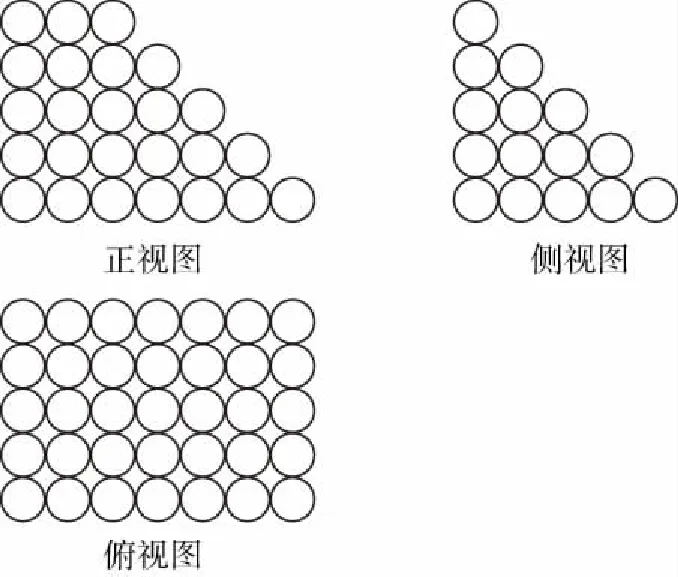
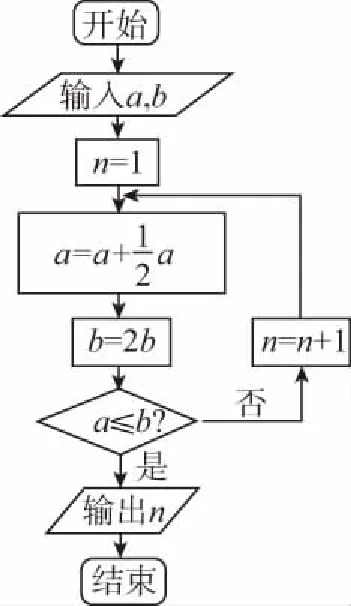
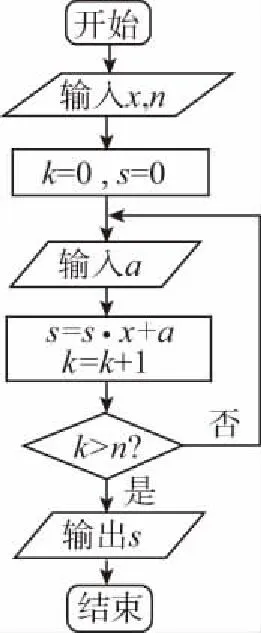
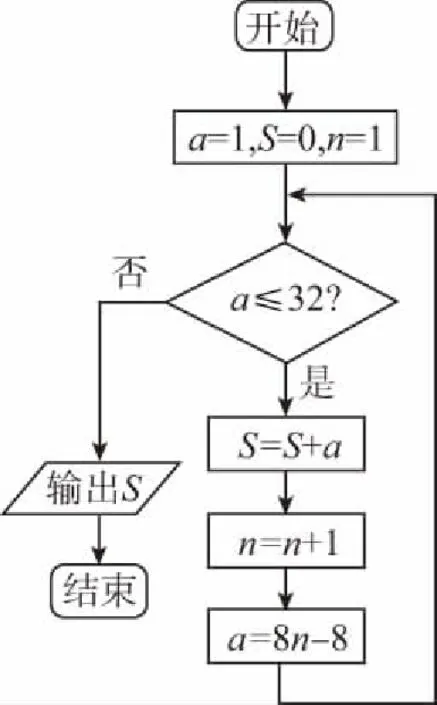
1.(2017·广东深圳一模)祖冲之之子祖暅是我国南北朝时代伟大的科学家,他在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”.意思是,如果两个等高的几何体在同高处截得的截面面积恒等,那么这两个几何体的体积相等.此即祖暅原理.利用这个原理求球的体积时,需要构造一个满足条件的几何体,已知该几何体三视图如图所示,用一个与该几何体的下底面平行相距为h(0 ( ) A.4π B.πh2 C.π(2-h)2D.π(4-h2) 【解析】由三视图知,这是一个底面半径为2,高为2的圆柱挖去一个底面半径为2高为2的圆锥,所以平行底面的平面截得一个圆环,其面积为两个圆面积之差.根据比例关系知截圆锥所得圆的半径为h,所以截面面积为4π-π·h2=π(4-h2),故选D. ( ) A.83 B.84 C.85 D.86 3.(2017·广东广州综合测试)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P-ABC为鳖臑,PA⊥平面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球O的球面上,则球O的表面积为 ( ) A.8π B.12π C.20π D.24π ( ) A.14 B.56 1.(2017·重庆模拟)我国古代数学算经十书之一的《九章算术》有一衰分问题:今有北乡八千一百人,西乡七千四百八十八人,南乡六千九百一十二人,凡三乡,发役三百人,则北乡遣 ( ) A.104人 B.108人 C.112人 D.120人 ( ) A.866 B.500 C.300 D.134 3.(2017·四川简阳检测)齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马.现从双方的马匹中随机各选一匹进行一场比赛,则齐王的马获胜概率为 ( ) 1.(2017·湖北荆、荆、襄、宜四地七校联考)我国古代宋元时期的数学名著《算学启蒙》里有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序框图,若输入的a,b分别为6,2,则输出的n为 ( ) A.2 B.3 C.4 D.5 【解析】第一次运行后: a=6+3=9,b=2×2=4,a>b,n=2; 第二次运行后: 第三次运行后: 第四次运行: 满足a≤b,结束程序;故输出n=4,故选C. 2.(2017·贵州黔东南州模拟)秦九韶是我国南宋时期著名的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为3,每次输入a的值均为4,输出s的值为484,则输入n的值为 ( ) A.6 B.5 C.4 D.3 【解析】由程序框图, 得s=4,k=1; s=4×3+4=16,k=2; s=16×3+4=52,k=3; s=3×52+4=160,k=4; s=160×3+4=484,k=5,结束循环,从而输入n的值为4,故选C. 3.(2017·福建莆田质检)我国古代数学著作《孙子算经》中有如下问题:“今有方物一束,外周一匝有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为 ( ) A.121 B.81 C.74 D.49 【解析】满足a≤32,第一次循环:S=1,n=2,a=8;满足a≤32,第二次循环:S=9,n=3,a=16;满足a≤32,第三次循环:S=25,n=4,a=24;满足a≤32,第四次循环:S=49,n=5,a=32;满足a≤32,第五次循环:S=81,n=6,a=40;接下来,因不满足a≤32,所以循环结束,输出S=81,故选B. 1.(2017·重庆月考)欧拉公式eix=cosx+isinx(i为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”,根据欧拉公式可知,e2i表示的复数在复平面中位于 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 ( ) 2.(2017·河北承德期中)远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.下图所示的是一位母亲记录的孩子自出生后的天数,在从右向左依次排列的不同绳子上打结,满七进一,根据图示可知,孩子已经出生的天数是 ( ) A.336 B.510 C.1 326 D.3 603 【解析】由题意满七进一,可得该图示为七进制数,化为十进制数为1×73+3×72+2×7+6=510,故选B.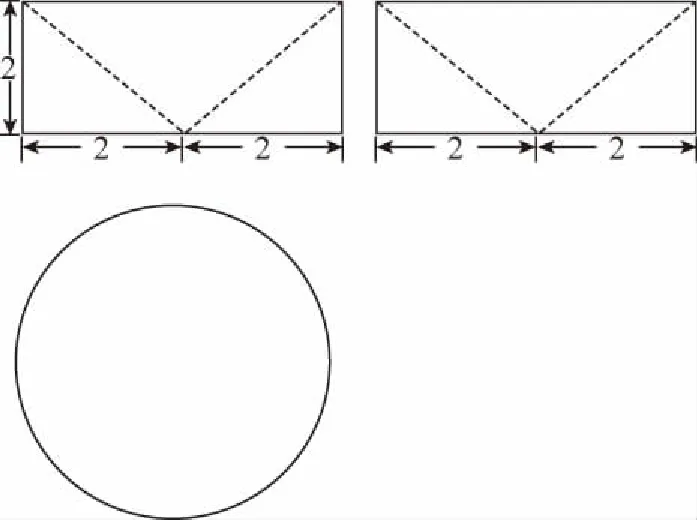
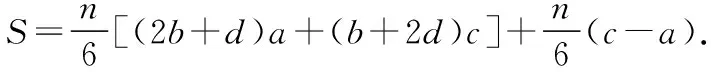
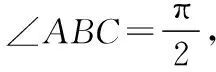
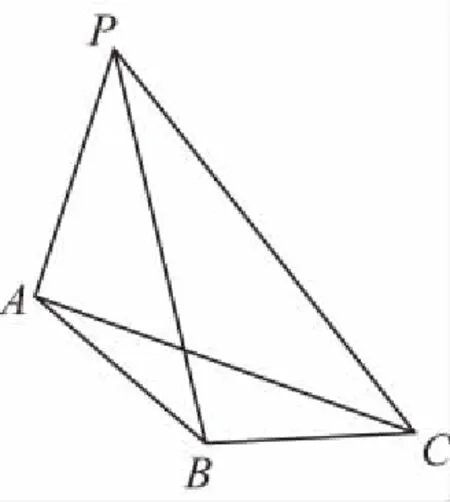
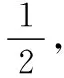
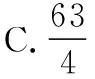
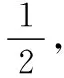
六、以解析几何为背景的数学文化题
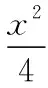
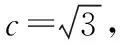
七、以统计概率为背景的数学文化题
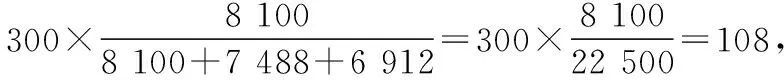
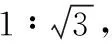
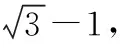
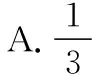
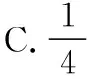
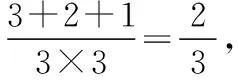
八、以算法为背景的数学文化题
九、以复数为背景的数学文化题
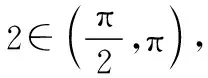
十、以推理证明为背景的数学文化题