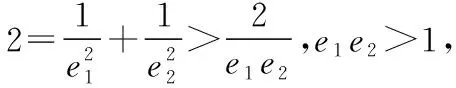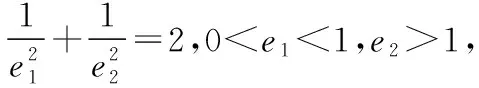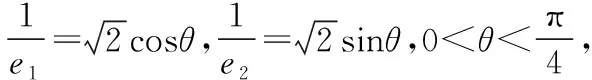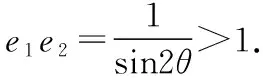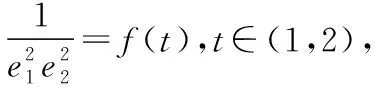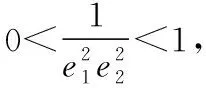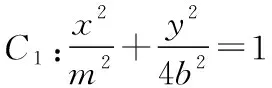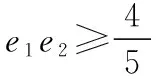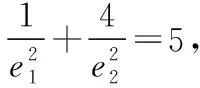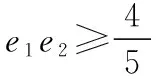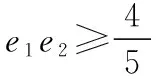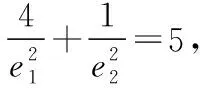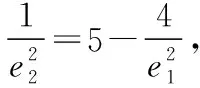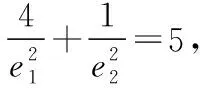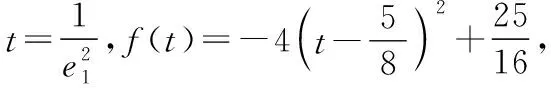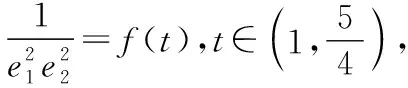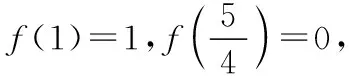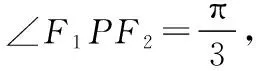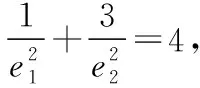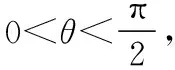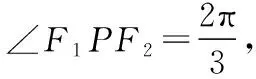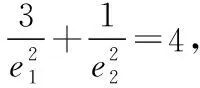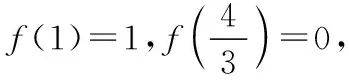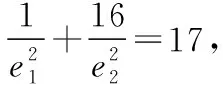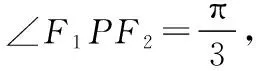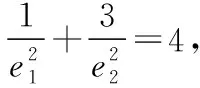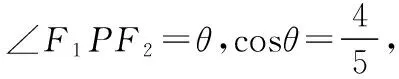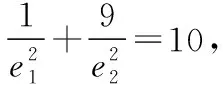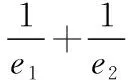共焦点的椭圆与双曲线的两个优美结论
2018-07-20湖北聂文喜
湖北 聂文喜
在近年高考及全国各地模拟考试中,频繁出现以共焦点的椭圆与双曲线为背景的两离心率之积与两离心率倒数之和的最值与范围问题,学生面对此类问题往往束手无策,本文介绍与此类问题有关的两个优美结论,通过具体例子说明结论的应用,供同学们复习时参考.
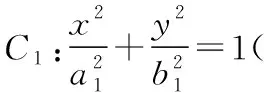
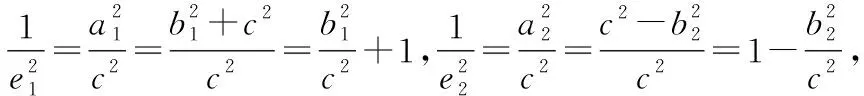
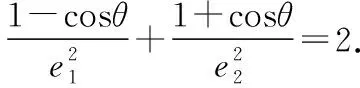

设P为椭圆与双曲线在第一象限内的公共点,F1,F2分别为左、右焦点,
则|PF1|+|PF2|=2a1,|PF1|-|PF2|=2a2,
∴|PF1|=a1+a2,|PF2|=a1-a2,
在△PF1F2中,由余弦定理得
|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cosθ,
∴4c2=(a1+a2)2+(a1-a2)2-2(a1+a2)(a1-a2)cosθ,
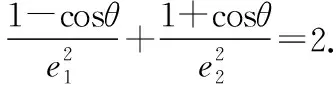
在解决以共焦点的椭圆与双曲线为背景的两离心率之积与两离心率倒数之和的最值与范围问题,利用结论1与结论2可以迅速找到解题思路,优化解题过程,起到事半功倍的效果.

( )
A.m>n且e1e2>1 B.m>n且e1e2<1
C.m 【解】设P为椭圆与双曲线在第一象限内的公共点, F1,F2为它们的左、右公共焦点, 则|PF1|+|PF2|=2m,|PF1|-|PF2|=2n,∴m>n, 方法1(利用均值不等式) 方法2(利用三角换元) 方法3(利用消元法) f(t)在(1,2)上单调递减,f(1)=1,f(2)=0, 【点评】如果已知b1与b2或b1与b2的倍数关系,则可由结论1得到e1与e2的等量关系式,于是问题转化为二元条件最值或范围问题,利用求二元条件最值的基本方法(如均值不等式、三角换元、消元法)使问题获解. ( ) ( ) 故选B. 【点评】一般情况下,若b1≥b2,则用例1的三种方法均可求出e1e2的取值范围,若b1 ( ) 方法1(利用柯西不等式)由柯西不等式得 ( )