回眸教材习题,提高解题能力
——平面向量的数量积二轮复习思考与实践
2018-07-20安徽蒋秀梅
安徽 蒋秀梅
波利亚说:“中学数学教学的首要任务是加强解题的训练”.数学解题教学是高三复习课的重点和核心目标,众所周知,高考命题的依据是教材,因此教材是高三复习选题的根本,二轮复习还要重视梳理知识点,这时尤其要注意紧密联系课本,不能脱离课本,不但要善于从课本中总结显性的知识,还要善于挖掘课本题目的隐含知识、延伸知识.
在平面向量这一章的复习过程中,由于向量来源于物理,向量的本质是既有大小又有方向的量,这揭示了向量兼具“数”与“形”的特点,所以复习过程中抓住“数”和“形”这两条线,明确向量是沟通数与形的桥梁.在平面向量基本定理的基础上,给出了平面向量的正交分解及坐标表示,坐标表示使平面中的向量与它的坐标建立起了一一对应的关系,由此将平面向量代数化,同时向量也是解决几何问题的有力工具.平面向量的数量积是每年高考的重点和热点内容,常常与三角函数、数列、解三角形、解析几何等交汇命题,解答此类问题往往利用向量的双重身份:转化为代数运算,或者利用向量的几何意义.通过对课本知识的梳理,我们可以发现课本上在“明”的方面提到了平面向量的数量积的三种计算方法:①定义法:a·b=|a||b|cosθ,θ=〈a,b〉;②坐标法:a·b=x1x2+y1y2,其中a=(x1,y1),b=(x2,y2);③投影法(几何意义).此外在“暗”的方面我们还可以挖掘出平面向量的数量积的两种计算方法;④基底法;⑤极化恒等式.
下面通过解读教材、领会教材、总结感悟三个环节谈谈平面向量数量积二轮复习的思考与实践.
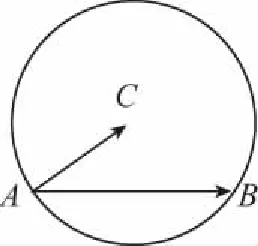
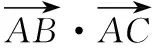
领会教材:本题可以帮助学生加深理解数量积概念的本质.
代数特征:a·b=|a||b|cosθ,其中θ=〈a,b〉,数量积的运算结果是一个数.
几何意义:数量积a·b等于a的长度|a|与b在a方向上的投影|b|cosθ的乘积.
【解析】取BC中点D,过G作GN⊥AH于N,
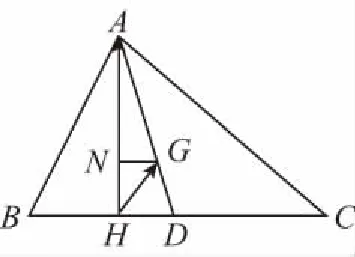
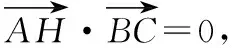
可得AH⊥BC.
故GN∥BC,

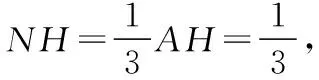
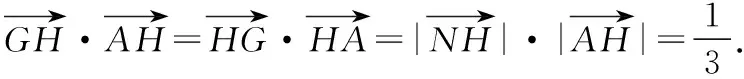
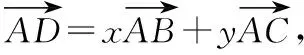
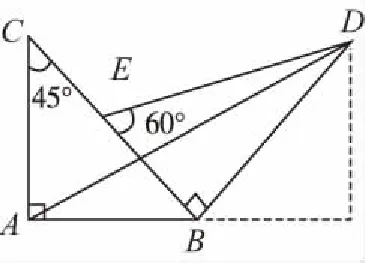
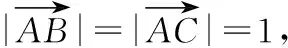
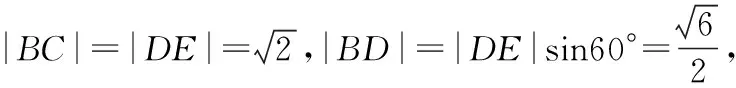


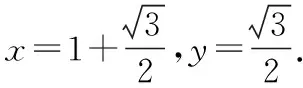
总结感悟:当数量积中有一个向量的长度为定值或投影与另一向量的长度关系确定时可以用平面向量的数量积的投影法解决问题,此法可将两不共线的向量问题转化为共线向量去解决,从而有效避免了cos〈a,b〉的计算.
教学片断2解读教材:教材第105页例3.已知|a|=6,|b|=4,a与b的夹角为60°,求(a+2b)·(a-3b).
如果我们换一种问法:已知|a|=6,|b|=4,a与b的夹角为60°,c=a+2b,d=a-3b,求c·d.就可以看成是以已知向量a,b为基底表示c,d进而求出c·d.
领会教材:本题的设置虽然并没有直指基底法,但是稍作改动就可以结合之前学习的平面向量基本定理视为用已知两个不共线的向量表示所求向量,再求数量积.
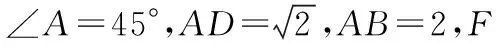
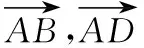
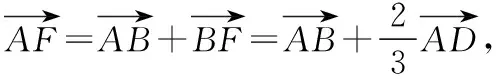
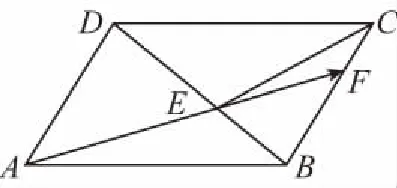
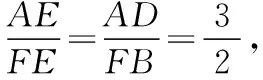
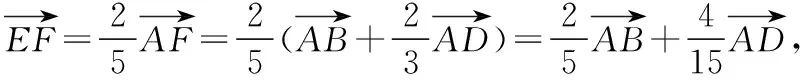
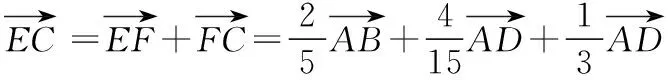
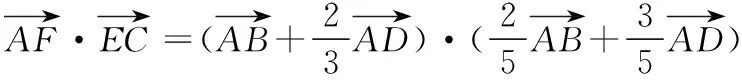
【变式训练2】设平面向量α,β满足|α+2β|=3,|2α+3β|=4,则α·β的最小值为________.
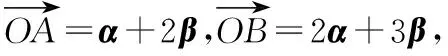
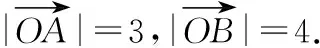
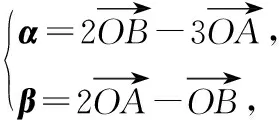
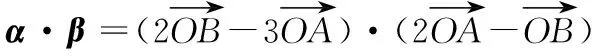
=-170,

总结感悟:题设条件中若给出了两个不共线的向量的模长和夹角,往往考虑选择其作为基底,将其他向量用这两个向量线性表示,问题转化成关于已知向量的计算.
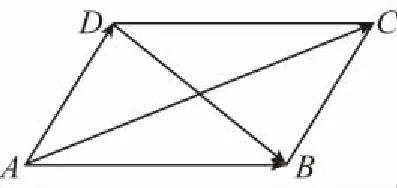

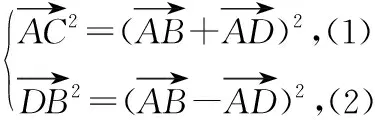
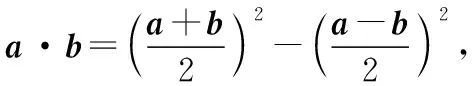
领会教材:这一题蕴含的数学思想比较多,首先,由于向量的线性运算和数量积运算具有鲜明的几何背景,平面图形的许多性质,如平移、全等、相似、长度、夹角等都可以由向量的线性运算计算出来,特别是数量积主要涉及向量的模以及向量的夹角,因此可以用向量方法解决平面几何中的一些问题;其次,在向量的线性运算中,两向量的加、减结果仍是一个向量,也可以认为是将多个向量的计算转化为单个向量,可以视为化简;最后,此题在运算过程中为了得到向量的长度关系将(1)+(2)消去了a·b,如果将(1)-(2)就转化为a·b的计算问题,启发学生转换看问题的角度,多角度思考问题,也能收到“他山之石可以攻玉”的效果.
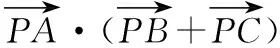
( )
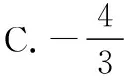
【解析】如图所示,取BC中点D,
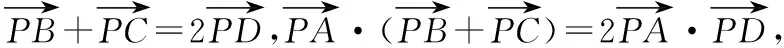
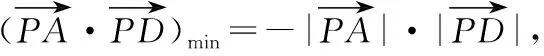
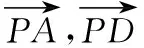

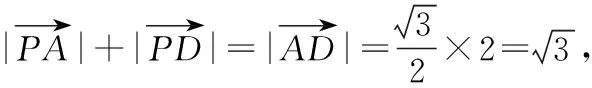
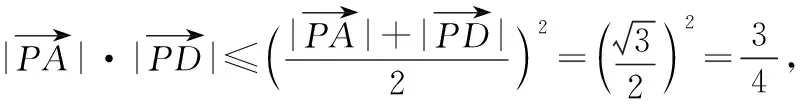
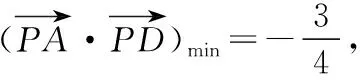
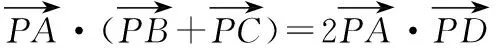
故选B.
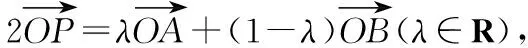
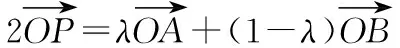
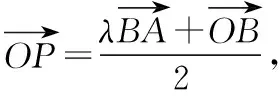


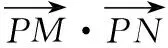

( )
A.0 B.2
C.3 D.6

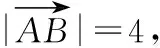
点A,B分别在直线x=1,x=3上,
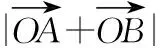
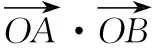
解法二(坐标法) 点A,B分别在直线x=1,x=3上,
设点A(1,y1),B(3,y2),
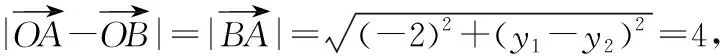
所以(y1-y2)2=12 ①,


则当且仅当(y1+y2)2=0 ②,
由②-①得y1y2=-3,
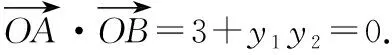
总结感悟:当遇到共起点的两不共线向量数量积问题时可以考虑转化为两向量的中线向量,也就是化多个向量为单个向量问题,进而运用极化恒等式处理相关问题.此外问题中如果含有矩形(正方形),等腰(等边)三角形,菱形以及其他具有垂直关系的图形,或者是考查函数图象上的点,以及解析几何相关问题都可以考虑采用坐标法,建立合适的坐标系利用坐标运算将有利于我们解决向量及几何问题.
教学片断4第108页A组第4题.求证:(λa)·b=λ(a·b)=a·(λb).
此题说明向量数量积具有数乘结合律,因λ数值不确定,证明过程应分三类讨论,体现了分类讨论的数学思想,同时在这三种运算顺序下结果是相同的,那么在有些问题中就可以将利用这个结论求出参数λ的值.
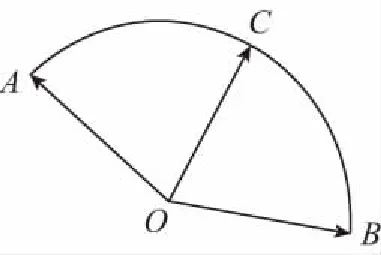

【解析】解法一 设∠AOC=α,则0°≤α≤120°,
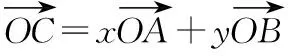
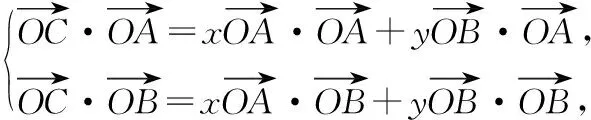
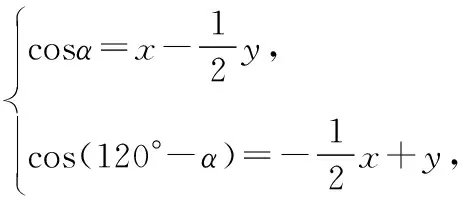
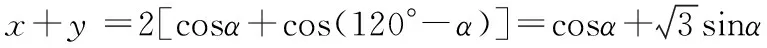
故x+y的最大值为2.
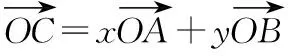
即x2+y2-xy=1.
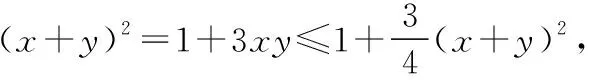
又x>0,y>0,解得x+y≤2.
当且仅当x=y时取“=”.故x+y的最大值为2.
解法三 以O为坐标原点,OB所在直线为x轴,与OB垂直的直线为y轴建立直角坐标系,则
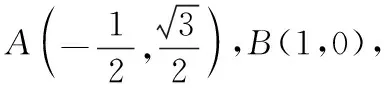
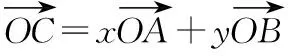

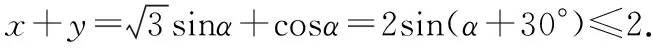
二轮复习重在提高学生的解题能力,但不能只顾埋头做题,更要重视考查知识的来龙去脉,通过对教材知识的梳理、总结、提炼让学生领会到教材是一切题源的根本,是一笔宝贵的财富,在题海中沉浮不如回眸教材会有一种“山穷水尽疑无路,柳暗花明又一村”的惊喜感,学会挖掘课本中更多的财富,从而实现整合知识网络,锻炼思维,提高解题能力的目标.
