数学极值法在圆周运动模型中的应用例析
2018-07-20广东任富华
广东 任富华
一、往年模拟试题例析
【例题1】(2016年广东佛山顺德适应性考试物理试题第4题)如图1所示,内壁光滑质量为m的管形圆轨道,竖直放置在光滑水平地面上,恰好处在两固定光滑挡板M、N之间,圆轨道半径为R;质量为m的小球能在管内运动,小球可视为质点,管的内径忽略不计。当小球运动到轨道最高点时,圆轨道对地面的压力刚好为零,下列判断正确的是
( )

图1
A.圆轨道对地面的最大压力大小为8mg
B.圆轨道对挡板M、N的压力总为零
D.当小球离挡板N最近时,圆轨对挡板N的压力大小为5mg
【答案】A
【例题2】[宁夏银川一中2017届高三考前适应性训练(一)物理试题第7题]如图2所示,内壁光滑的圆管形轨道放在光滑水平地面上,且恰好处在两固定光滑的挡板M、N之间,圆轨道半径为R,其质量为2m,一质量为m的小球能在管内运动,小球可视为质点,管的内径不计,当小球运动到最高点时,圆轨道对地面的压力刚好为零,则下列判断正确的是
( )

图2
B.圆轨道对地面的最大压力大小为10mg
C.当小球离挡板N最近时,圆轨对挡板N的压力大小为5mg
D.圆轨道对挡板M、N的压力总为零
【答案】BC
以上两个例题用的是同一个物理模型,考查的知识点也是一样的。
【例题1解析】小球经过最高点时圆轨道对地面的压力为零,可知小球对圆轨道的作用力等于圆轨道受到的重力,由牛顿第三定律和牛顿第二定律可知:

小球从最高点运动到离挡板N最近时,由机械能守恒定律有:

圆轨道对小球的作用力提供小球的向心力,有:

由①②③三式解得圆轨道对挡板N的压力:
N1′=N1=4mg
小球从最高点运动到最低点,由机械能守恒有:

小球在最低点,合外力提供向心力,有:

解得小球在最低点对圆轨道的压力:N2′=N2=7mg
所以圆轨道对地面的压力:N3=N2′+mg=8mg。
例题2与例题1解法相同,在此不再赘述。
二、分析模型,提出问题
由于以上物理模型能较好地考查学生的综合能力,利用网络搜索不难发现,不少学校都用了这个物理模型,或直接引用,或修改了已知条件。学生解题时,关注的是用什么样的物理定律、定理和方法,对物理模型本身的合理性不会质疑。物理教师解题或编题时,不仅要知道解题的方法,更要关注物理模型本身的合理性。物理模型往往是理想化的,但并不是空想而来、随意捏造,而是对实际问题的抽象,它必须符合物理规律,可以被人们的思维所接受。
就以上物理模型,可以进行这样问答式的定性辨析:小球过圆轨道最高点时,圆轨道为何会对地面的压力刚好为零?因为小球对圆轨道竖直向上的作用力等于圆轨道受到的重力;小球的位置不是在圆轨道最高点时,可不可以使圆轨道对地面的压力刚好为零?可以,小球给圆轨道斜向上的作用力,当此力在竖直方向的分力等于圆轨道受到的重力时,圆轨道对地面的压力为零,如图3所示;小球从A向B运动过程中,速度大小怎么变化?向心力大小怎么变?小球的速度减小,小球的向心力变小;小球对轨道的弹力大小怎么变化?从A到B,分析小球,设圆轨道对小球的作用力为F,由牛顿第二定律可知:F+mgcosθ=F向,F向减小,mgcosθ增大,故F一定减小,由牛顿第三定律可知F′一定减小;小球对圆轨道作用力的竖直分力怎么变?小球对圆轨道的竖直分力就是图3中Fy,Fy=F′cosθ,小球从A到B的运动过程中,F′在减小,cosθ在增大,故不能直接判断竖直分力Fy怎么变化。

图3
通过以上辨析可知,小球对圆轨道的竖直分力最大值不一定在最高点。若在最高点之前的某个位置出现最大值,题目中“当小球运动到最高点时,圆轨道对地面的压力刚好为零”就是一个错误的设定,实际上小球在达到最高点之前,小球对圆轨道的竖直分力已经大于了圆轨道受到的重力,圆轨道离开了地面。那么,到底是不是在小球经过最高点时出现最大的竖直分力呢?若不是在最高点出现最大的竖直分力,又是在什么位置?要解决以上问题,需要利用数学极值法定量研究。
三、利用数学极值法解决问题
我们来研究例题2,假设“当小球运动到最高点时,圆轨道对地面的压力刚好为零”是正确的。如图4所示,设小球在最高点的速度为v1,在P点的速度为v2,根据机械能守恒有:

图4

由于小球运动到最高点时,圆轨道对地面的压力刚好为零,可知小球对圆轨道的作用力等于圆轨道受到的重力,由牛顿第三定律和牛顿第二定律可知,小球在最高点有:

小球运动到P点时受力分析如图4,有:

由①②③三式结合牛顿第三定律可解得小球对圆轨道的作用力:
F′=F=5mg-3mgcosθ
小球对圆轨道的竖直分力:
Fy=F′cosθ=5mgcosθ-3mgcos2θ

以上结论告诉我们,在假设成立的情况下,小球在达到最高点之前圆轨道已经离开了地面,不符合题意。故题中“当小球运动到最高点时,圆轨道对地面的压力刚好为零”的设定是不正确的。
为了进一步研究问题,设小球的质量为m,圆轨道的质量为M,仍假设“当小球运动到最高点时,圆轨道对地面的压力刚好为零”是正确的,有:

由①③④三式结合牛顿第三定律可解得小球对圆轨道的作用力:
F′=F=(3mg+Mg)-3mgcosθ
小球对圆轨道的竖直分力:
Fy=F′cosθ=(3mg+Mg)cosθ-3mgcos2θ
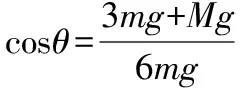
因此,对于本文给出的两个例题研究的物理模型来讲,设圆轨道质量为M,小球质量为m,为了严谨规范,无科学性错误,在设定质量时,应让圆轨道质量大于或等于小球质量的3倍,即:M≥3m。

