平台稳定回路模糊PI参数在线调整控制
2018-07-20赵军虎
王 卿,王 汀,赵军虎,胡 贞
(1.长春理工大学电子信息工程学院,长春130022;2.北京航天控制仪器研究所,北京100039)
0 引言
惯导稳定平台是平台式惯性导航、制导的核心,而平台稳定回路保证了平台台体能够稳定于惯性空间并且按要求跟踪预定方位[1]。所以,提高稳定回路的性能对提高平台式惯导系统的精度有重要意义。
目前,稳定回路的控制实现方法多种多样,但实际应用的多是经典控制,如PID控制、超前滞后控制等。但是常用的超前滞后控制仍存在很多局限性,如动态性能欠佳等。本文在经典控制基础上提出一种基于模糊逻辑的PI参数自适应控制方法,经仿真验证表明控制性能有一定改善。
1 稳定回路建模及原理
1.1 稳定回路工作原理
以台体轴(Z)为例,当其受到干扰力矩时,台体轴转动引起Z陀螺仪输出轴产生转角β。然后通过角度传感器、相敏解调、前置放大电路转换成直流电压信号,再经校正网络校正,最后由功放电路驱动台体轴力矩电机产生控制力矩以抵消干扰力矩产生的转角,完成稳定功能。
1.2 模型建立
如图1所示,稳定回路中各环节传递函数建立如下:
由稳定回路模型可得其开环传递函数为:
设定J= 0.030kg·m2、I= 2×10-5kg·m2、H=0.029N·m·s、D= 1× 10-2kg·m2/s、Kg=0.36N·m/A、Tg=0.57ms,代入参数可得到被控对象的开环Bode图,如图2所示。
由开环Bode图可看出其稳定裕度为4.23°,幅值裕度为7.23dB。
2 超前滞后控制
由图2可知,无较正网络的被控对象系统稳定,但指标达不到要求,根据调节时间、幅值裕度和相位裕度[2]的要求设计校正网络。由于要求无静差,须添加1阶纯积分,相应需增加零点使系统稳定,仅增加一个零点仍无法满足剪切频率的要求,所以须再加零点,此时分子阶数高于分母须增加极点,这样就确定了校正网络的形式:
设置参数k1= 1/20、k2= 1/43、k3= 1/20、k4=1/1300。取0.1 N·m干扰力矩,系统的阶跃响应仿真结果如图3所示,其开环Bode图如图4所示。
结果表明此种控制方法超调量达到42.8%,调节时间为0.05s,相位裕度为39.6°,幅值裕度为15.9dB。
对校正网络参数进行调整得:k1=1/20、k2=1/20、k3=1/15、k4=3/4000,仿真结果如图5、图6所示。
调整后超调有所减小,超调量为28.5%,调节时间基本还为0.05s,相位裕度为49.3°,幅值裕度为16.6dB。
由上述分析可知,超前滞后控制在控制器形式确定后,手动不断仿真调整参数可以使性能优化,但超调仍达到将近30%。下面分析模糊PI参数在线调整控制的控制效果。
3 模糊PI参数调整控制
3.1 模糊控制器
模糊控制在一定程度上模仿人的控制,属于智能控制的范畴。基于Mamdani模型的模糊控制系统由模糊化、知识库、模糊推理和反模糊化几部分组成[3-4],如图7所示。
3.2 模糊PI控制
在PID控制基础上,采用误差及误差变化率为输入,Δkp、Δki为输出的二维模糊控制器,利用模糊逻辑推理方法在线调整P、I参数值而保持微分环节不变,实现自适应控制。
(1)隶属函数
输入信号误差的论域为(-1,1),误差变化率论域为(-1,1),输出信号 Δkp、Δki的论域分别为(- 0.1,0.1)、(- 0.1,0.1)。 语言变量取负大(NB)、负中(NM)、零(ZE)、正 中(PM)、正 大(PB),比例因子和量化因子均取1。隶属函数均选取三角形函数,各输入输出的隶属函数曲线如图8所示。
(2)模糊规则
MIMO模糊控制规则可分解成多个MISO字库[5],相应每条模糊规则的逻辑运算[6]为:
式中,Ri为模糊规则集,Ai、Bi为各输入论域对应模糊集,Ci为输出论域对应模糊集。
由经验知识及对系统的分析知,当偏差e很大时,系统应消除偏差并以快速性为主,此时使系统响应需有快速跟踪特性,选择较大Kp,较小Ki;当e中等大小时,考虑减小超调量及振荡次数,此时应取偏小的K以及取适中的Ki;e值趋于0时,取较大的Kp值同时Ki可以取大一些,使系统具有较好的稳态性能,并可以避免出现振荡现象。当e′值变大时,适当减小Kp值,加大Ki值。在开始调节时,为增加系统快速性增大Kp;在调节过程中期,适当减小Kp取值,以降低系统的超调量同时保证系统快速性;在调整后期,为减小静差同时保证系统的稳定性能,此时可Kp值取相对大。
模糊规则表如表1、表2所示。
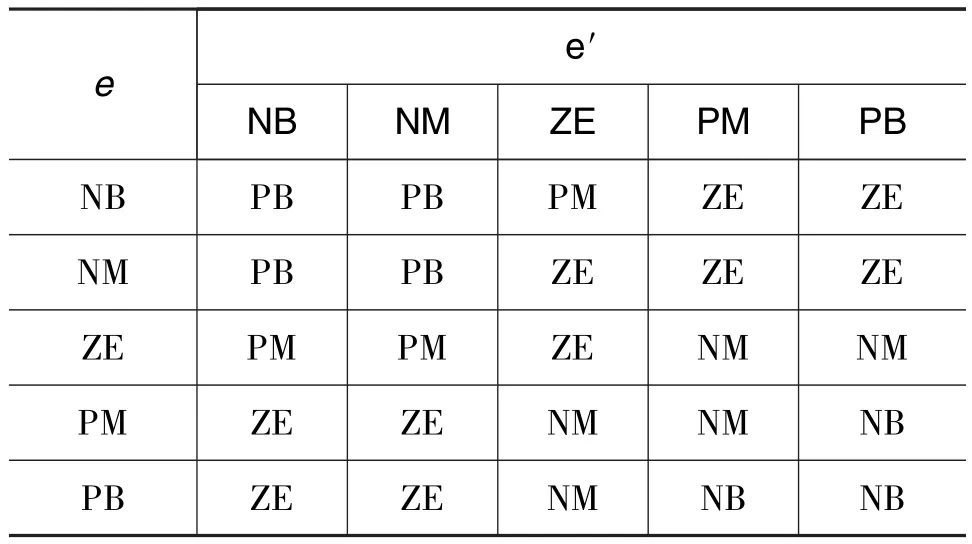
表1 ΔKp模糊规则Table 1 Fuzzy rules of ΔKp

表2 ΔKi模糊规则Table 2 Fuzzy rules of ΔKi
(3)反模糊化
通过模糊推理得到的结果是模糊量,实际控制需将模糊量清晰化,这就是反模糊化过程。反模糊计算方法有重心法、最大隶属度法、中位数法等[7-8],重心法指取模糊集合隶属度函数曲线同基础变量轴所围面积的中心对应的元素作为清晰化后的精确值结果,计算复杂,在模糊集合为不规则图形时积分运算将十分困难;中位数法选取使得隶属函数曲线和横坐标所围成区域面积平分的数作为去模糊结果,忽略了隶属度较大的元素的主导作用;而最大隶属度法运算简单,能够突出隶属度大元素的影响,经仿真能满足控制要求。所以本文采用最大隶属度法进行反模糊化。
若输出量模糊集合C′的隶属函数只有一个峰值,则取隶属函数的最大值为清晰值,即:
式中,z0为清晰值。
若C′的隶属函数有多个极值,则取这些极值的均值为清晰值[9-10]。
3.3 仿真结果
以台体轴为例,为比较本文设计的含微分模糊PI控制与传统超前滞后算法对轴端干扰力矩的抑制作用,用阶跃输入信号来模拟稳定回路的干扰力矩进行仿真。设稳定回路台体轴干扰力矩为0.1N·m,仿真框图如图 9所示,仿真结果如图10、图11所示。
结果显示,当加入扰动后,运用含微分的模糊PI参数自整定控制,控制力矩超调为10.7%,减少了 17.8%,相位裕度为 60°,幅值裕度为20.4dB。模糊PI参数自整定控制动态响应特性优于超前滞后控制。
4 结论
本文设计了含微分的模糊PI参数在线调整控制方法,并通过计算机仿真将其与超前滞后控制方法进行了比较。结果表明,前者可改善传统超前滞后控制超调大的问题,提升系统动态性能,提升稳定回路抗干扰能力。
